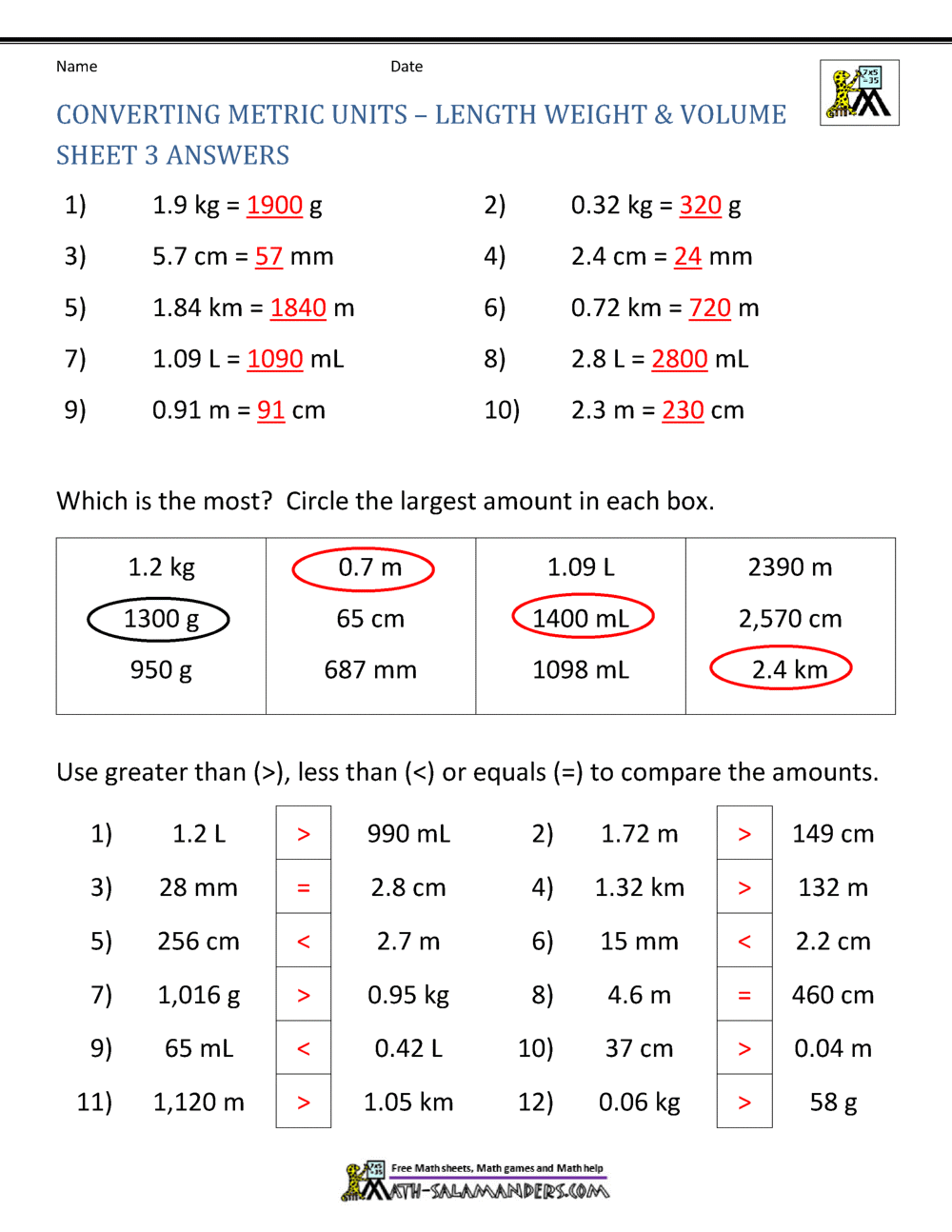
5 Inequality Word Problems Worksheets for Math Mastery

When it comes to mastering mathematics, understanding and solving inequality word problems is a crucial skill. Not only do inequalities provide a foundation for more advanced mathematical concepts, but they are also incredibly practical in everyday life situations like budgeting, scheduling, and optimization. This blog post will delve into five carefully designed worksheets that aim to enhance your ability to tackle inequality word problems, making math mastery an achievable goal.
Why Focus on Inequality Word Problems?

Inequalities are mathematical expressions that compare two values or quantities, indicating that one is not equal to the other. This relationship can involve being greater than, less than, or any form of inequality in between. Here’s why focusing on these problems is beneficial:
- Practical Application: Inequalities are everywhere in real life. From setting a budget, understanding rate comparisons, to optimizing resource allocation, inequalities help in decision-making.
- Building Conceptual Understanding: Working through inequality word problems fosters a deeper understanding of how numbers relate to each other beyond simple equality.
- Critical Thinking: These problems require students to apply logic, interpret conditions, and translate real-world scenarios into mathematical models.
Worksheet 1: Basics of Inequalities

This worksheet introduces students to the fundamental concepts of inequalities:
- Understanding inequality symbols (>, <, ≥, ≤, ≠)
- Converting word problems into inequalities
- Graphing inequalities on a number line
Example Problem: John earns 10 per hour. If he wants to buy a video game that costs 55, how many hours (h) does he need to work?
📝 Note: In this problem, we translate "wants to buy" into "≥" because John would ideally like to work the minimum amount needed to buy the game.
| Problem | Equation | Solution |
|---|---|---|
| John's Earnings | 10h ≥ 55 | h ≥ 5.5 |

Worksheet 2: Inequalities with Two Variables

This worksheet elevates the complexity by introducing:
- Solving systems of inequalities
- Graphing regions on coordinate planes
- Finding intersection points of solutions
Example Problem: Kim needs to buy at least 25 apples and 30 oranges. If apples cost 0.50 each and oranges cost 0.75 each, how much money (m) does she need?
| Constraints | Inequalities |
|---|---|
| Apples | 0.50x ≥ 25 |
| Oranges | 0.75y ≥ 30 |
| Money Needed | m ≥ 0.50x + 0.75y |
Worksheet 3: Real-World Scenarios

Applying inequalities to practical situations is the focus here:
- Calculating optimal production in manufacturing
- Financial constraints and budgetary limitations
- Optimization of time for scheduling
Example Problem: A factory can produce up to 1200 widgets per day. If each widget can be made with two materials, A or B, and Material A costs 1.20 per widget while Material B costs 0.80, how many widgets of each type should be made to maximize profit while staying under a $1000 budget?
📝 Note: The solution involves linear programming techniques which are more advanced, but the focus here is on setting up the inequalities correctly.
Worksheet 4: Advanced Inequality Word Problems

This worksheet challenges students with more complex scenarios:
- Non-linear inequalities
- Solving systems involving absolute value
- Involving inequalities in calculus problems
Example Problem: The temperature on a certain planet changes according to the formula |T - 30| ≤ 25, where T represents the temperature in degrees Fahrenheit. What is the range of temperatures where organisms can survive?
Worksheet 5: Error Analysis and Proofs

The final worksheet aims to solidify understanding:
- Identifying common mistakes in inequality solutions
- Proofs involving inequalities (e.g., AM-GM Inequality)
Example Problem: Prove that for all positive numbers a, b, c, the inequality (a + b + c) / 3 ≥ (abc)^(1⁄3) holds true.
📝 Note: Proofs help students to think critically about the properties of inequalities.
By progressively working through these five worksheets, students can systematically build their proficiency in handling inequalities in word problems. These exercises not only promote understanding but also develop practical problem-solving skills, which are essential not just in mathematics but in everyday life. Whether you're planning to ace that upcoming math exam or looking to apply mathematical reasoning in real-world situations, these worksheets provide a solid foundation for inequality mastery.
How can students benefit from practicing inequality word problems?

+
Practicing inequality word problems helps students to better understand how to translate real-world situations into mathematical models, improve their critical thinking, and apply logical reasoning.
What are some common mistakes when solving inequality word problems?

+
Common mistakes include misunderstanding the inequality symbols, incorrectly graphing solutions, flipping the sign when multiplying or dividing by a negative number, or misinterpreting word problems.
Can inequality word problems be applied in fields outside of mathematics?

+
Absolutely! Fields like economics, engineering, computer science, and even personal finance use inequalities to solve problems involving constraints and optimization.