Solve Inequalities with Variables on Both Sides Easily

There's something thrilling about the challenge of solving inequalities with variables on both sides. Whether you're a student grappling with algebra or an engineer working on complex systems, mastering this skill can provide a sense of accomplishment and open doors to further mathematical exploration. But fret not, for this guide is designed to make this seemingly daunting task quite manageable.
Understanding Inequalities with Variables on Both Sides

In mathematics, an inequality compares two values, stating that one is less than, greater than, or not equal to the other. Here are some common inequality symbols:
- < : Less than
- > : Greater than
- ≤ : Less than or equal to
- ≥ : Greater than or equal to
- ≠ : Not equal to
Let's dive into how you can tackle inequalities with variables on both sides:
Step-by-Step Process

1. Write the Inequality

Begin with the inequality in question. For example:
$$3x + 5 > 2x - 3$$
2. Isolate the Variables on One Side

To streamline the process, you'll want all the x-terms on one side of the inequality. Here's how:
Step a: Subtract 2x from both sides:
$$3x + 5 - 2x > 2x - 3 - 2x$$Which simplifies to:
$$x + 5 > -3$$Step b: Now, subtract 5 from both sides:
$$x + 5 - 5 > -3 - 5$$This becomes:
$$x > -8$$Now our inequality is solved, with the variable x isolated on one side.
3. Interpretation and Final Touches
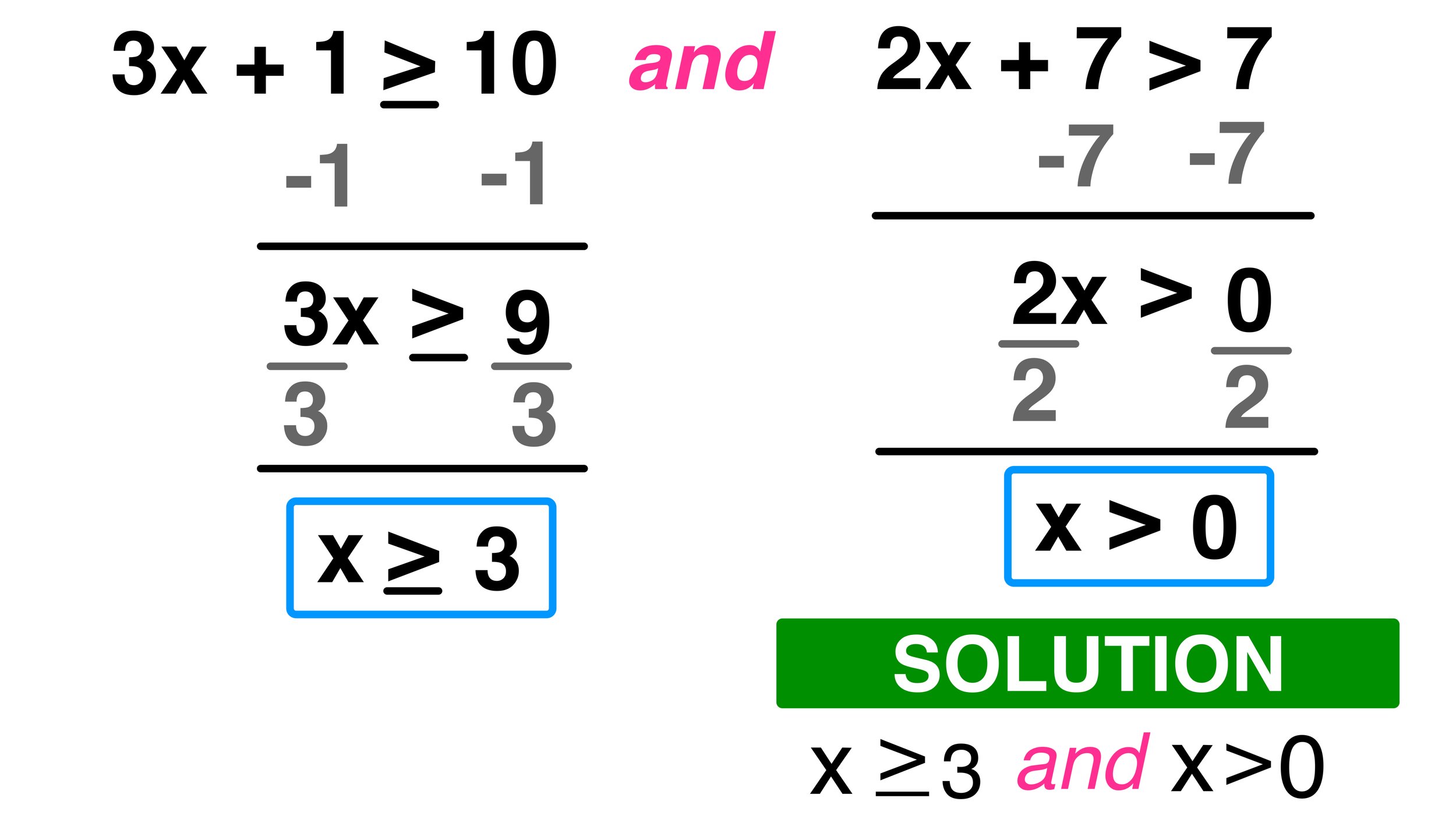
- If you've used division or multiplication by a negative number, remember to reverse the inequality symbol.
- Check your work by substituting different values of x to ensure they match the original inequality.
⚠️ Note: Multiplying or dividing both sides by a negative number flips the inequality sign.
Advanced Techniques

Using Interval Notation

When solving inequalities, you might need to express your solution using interval notation, especially when dealing with compound inequalities. Here's a quick overview:
| Interval Notation | Meaning |
|---|---|
| (a, b) | All numbers x such that a < x < b |
| [a, b] | All numbers x where a \le x \le b |
| (a, \infty) | All numbers x where x > a |

Compound Inequalities

Compound inequalities involve two inequalities joined by "and" or "or." Here's how to handle them:
- "And" Inequalities: Combine two inequalities to find the overlapping region.
- "Or" Inequalities: Take the union of the solutions sets from two separate inequalities.
Examples of Solving Compound Inequalities

Consider the inequality: 3 < 2x + 1 \le 5. To solve:
- Split into two separate inequalities:
- 3 < 2x + 1
- 2x + 1 \le 5
- Solve each individually:
- From 3 < 2x + 1, subtracting 1 from both sides gives: 2 < 2x or 1 < x
- From 2x + 1 \le 5, subtracting 1 from both sides yields: 2x \le 4 or x \le 2
- The solution is where both conditions hold true: 1 < x \le 2 or in interval notation (1, 2] .
To wrap things up, tackling inequalities with variables on both sides requires a methodical approach. Here's what we've learned:
- Recognize the fundamental inequality symbols and their meanings.
- Isolate the variable on one side by systematically moving terms to the opposite side.
- Be cautious when dealing with negative numbers; remember to flip the inequality symbol if necessary.
- Employ advanced techniques like interval notation for compound inequalities.
By following these steps, you'll not only solve inequalities efficiently but also deepen your understanding of algebraic manipulation, setting the stage for further mathematical success. Keep practicing, and soon, solving inequalities will become as natural as breathing.
Why do we need to reverse the inequality symbol?

+
Reversing the inequality symbol when multiplying or dividing by a negative number maintains the relationship between the two sides of the inequality, ensuring the solution remains consistent with the original inequality.
What does interval notation look like for compound inequalities?

+
For compound inequalities like (a < x < b), interval notation would be ((a, b)), showing all numbers (x) between (a) and (b), but not including (a) or (b). If (a \le x \le b), then it would be ([a, b]), including both endpoints.
How do I check if my inequality solution is correct?

+
Substitute values back into the original inequality to ensure they hold true. For example, for (x > -8), pick values like (x = -7) (should hold), (x = -8) (shouldn’t hold), and (x = -9) (shouldn’t hold), verifying your solution set.