5 Tips to Ace Parallel Lines Worksheet Geometry

Geometry is a fascinating subject that lays the foundation for understanding spatial relationships and provides the tools necessary to navigate and manipulate the physical world through the lens of mathematics. A significant part of studying geometry involves understanding the concept of parallel lines and their intersection with other lines, which introduces students to angles and their measurements. Whether you're a student preparing for a math quiz, or a teacher looking for ways to make geometry more engaging, mastering parallel lines worksheets can significantly improve your proficiency in this area. Here are five tips to help you excel in this aspect of geometry:
1. Understand the Basics of Parallel Lines


Before diving into the exercises, ensure you have a solid grasp of what parallel lines are:
- Parallel lines are lines in the same plane that do not intersect or meet at any point.
- They maintain an equal distance between each other at all points.
- The slopes of parallel lines are equal in a coordinate plane.
This basic understanding sets the groundwork for solving more complex problems involving these lines.
2. Master Angle Relationships

| Angle Type | Definition |
|---|---|
| Corresponding Angles | Angles that are on the same side of the transversal and in corresponding positions. |
| Alternate Interior Angles | Angles that are on opposite sides of the transversal but inside the two parallel lines. |
| Alternate Exterior Angles | Angles that are on opposite sides of the transversal but outside the two parallel lines. |
| Consecutive Interior Angles (Same-Side Interior) | Angles that are on the same side of the transversal and inside the two parallel lines. |
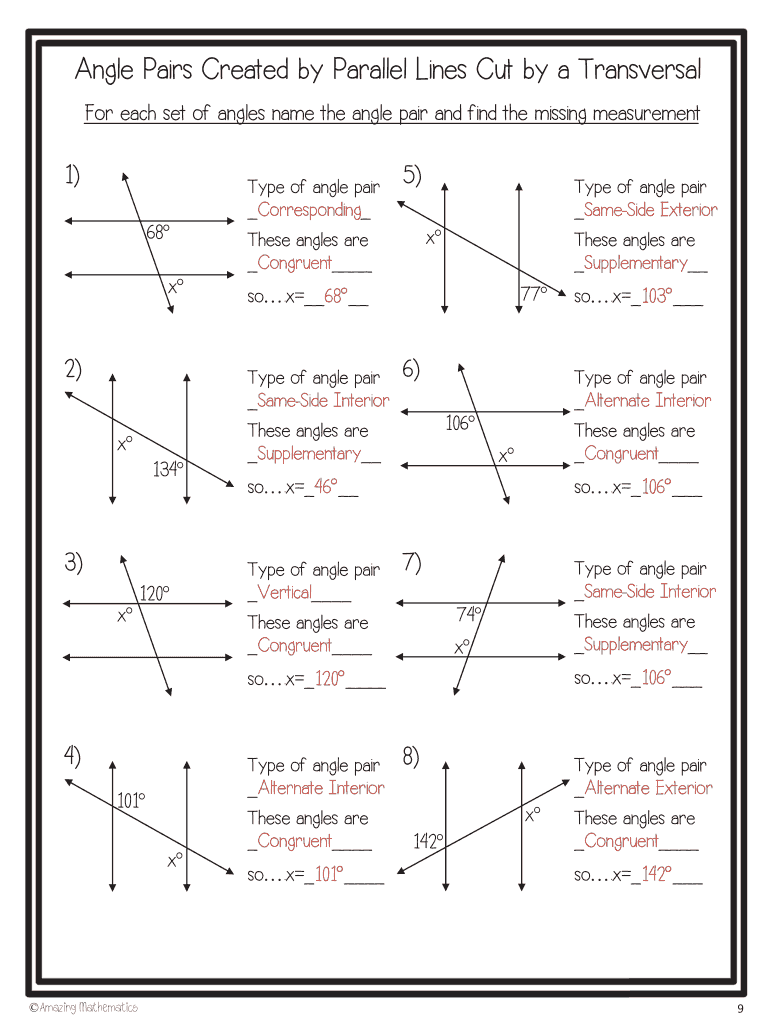
Each of these angle relationships has properties that can help you solve parallel lines problems:
- Corresponding Angles are equal.
- Alternate Interior and Exterior Angles are equal.
- The sum of Consecutive Interior Angles is always 180 degrees.
🔍 Note: Pay attention to the transversal line's position in relation to the parallel lines, as this affects the type of angles formed.
3. Practice Visualizing Problems


One of the best ways to understand geometry is through visualization:
- Draw diagrams to visualize the given information. This can make abstract concepts more tangible.
- Use different colors or patterns to distinguish between angles and lines to keep your work organized.
- Imagine moving around the problem as if you were in a 3D space; this helps in understanding how angles are formed.
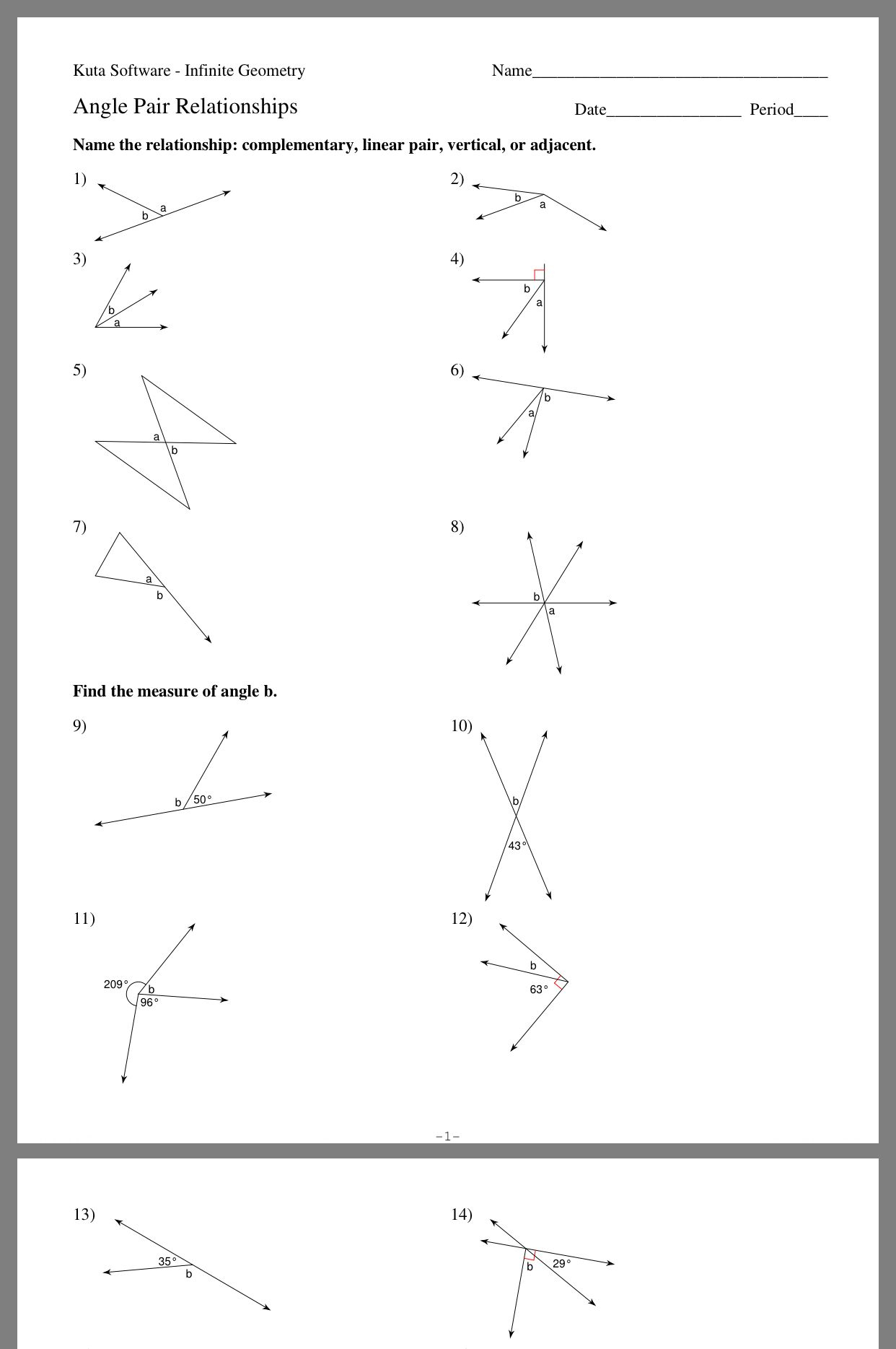
4. Solve Various Types of Problems

Geometry worksheets often include different types of problems. Here are a few you should focus on:
- Identifying Angle Types: You’ll need to name the angles formed by the intersection of a transversal with parallel lines.
- Finding Unknown Angles: Use the angle properties to solve for unknown angles when given some angle measures.
- Proofs: Show that lines are parallel by proving that corresponding, alternate, or consecutive angles satisfy the required conditions.
⚠️ Note: When solving proofs, always state the properties you're using and show each step clearly.
5. Review and Refine Your Methods

After tackling a set of problems:
- Go through your work and check for mistakes or missed steps.
- Look for patterns in your errors or areas where you consistently struggle. Address these through additional practice or by seeking clarification.
- Develop strategies like plugging in test values or simplifying complex problems into manageable parts.
By consistently employing these tips, you can significantly enhance your performance on parallel lines worksheets. Understanding the fundamental concepts, mastering angle relationships, practicing visualization, solving a variety of problems, and refining your approach will not only help you ace these worksheets but also foster a deeper understanding of geometry. This mastery can serve as a stepping stone for tackling more advanced geometric problems and real-world applications.
What is the importance of parallel lines in geometry?

+
Parallel lines are crucial in geometry because they help in understanding and defining other geometric figures and relationships, such as angles, transversals, and polygons. They are foundational for proofs and are used in real-life applications like architecture, engineering, and design.
How can I remember the properties of angles formed by parallel lines?
+
One effective method is to use mnemonics or acronyms. For instance, remember “CoCoA” for Corresponding, Alternate, Consecutive. Additionally, consistent practice and drawing diagrams can help solidify these properties in your memory.
Why do I sometimes struggle with parallel lines problems?

+
Struggles often come from not fully understanding the basic concepts or the relationships between angles. It could also be due to lack of practice, misinterpretation of diagrams, or not visualizing the problem correctly. Revisiting the basics, seeking help, and practicing regularly can help overcome these issues.



