5 Exponent Tricks You'll Love: Answer Key Revealed

If you're fascinated by the power of exponents, you're in for a treat. Here's a deep dive into 5 Exponent Tricks that can make mathematical calculations not only simpler but also more engaging. Whether you're a student trying to tackle algebra, or just someone curious about numbers, these tricks will surely add a dash of magic to your number crunching adventures.
Understanding Exponents

Before we delve into the tricks, let’s quickly recap what exponents are. An exponent, or power, represents how many times to multiply a number by itself. For instance, in the expression (2^3), 2 is the base and 3 is the exponent, which means 2 multiplied by itself three times: (2 \times 2 \times 2 = 8).

Trick #1: Negative Exponents
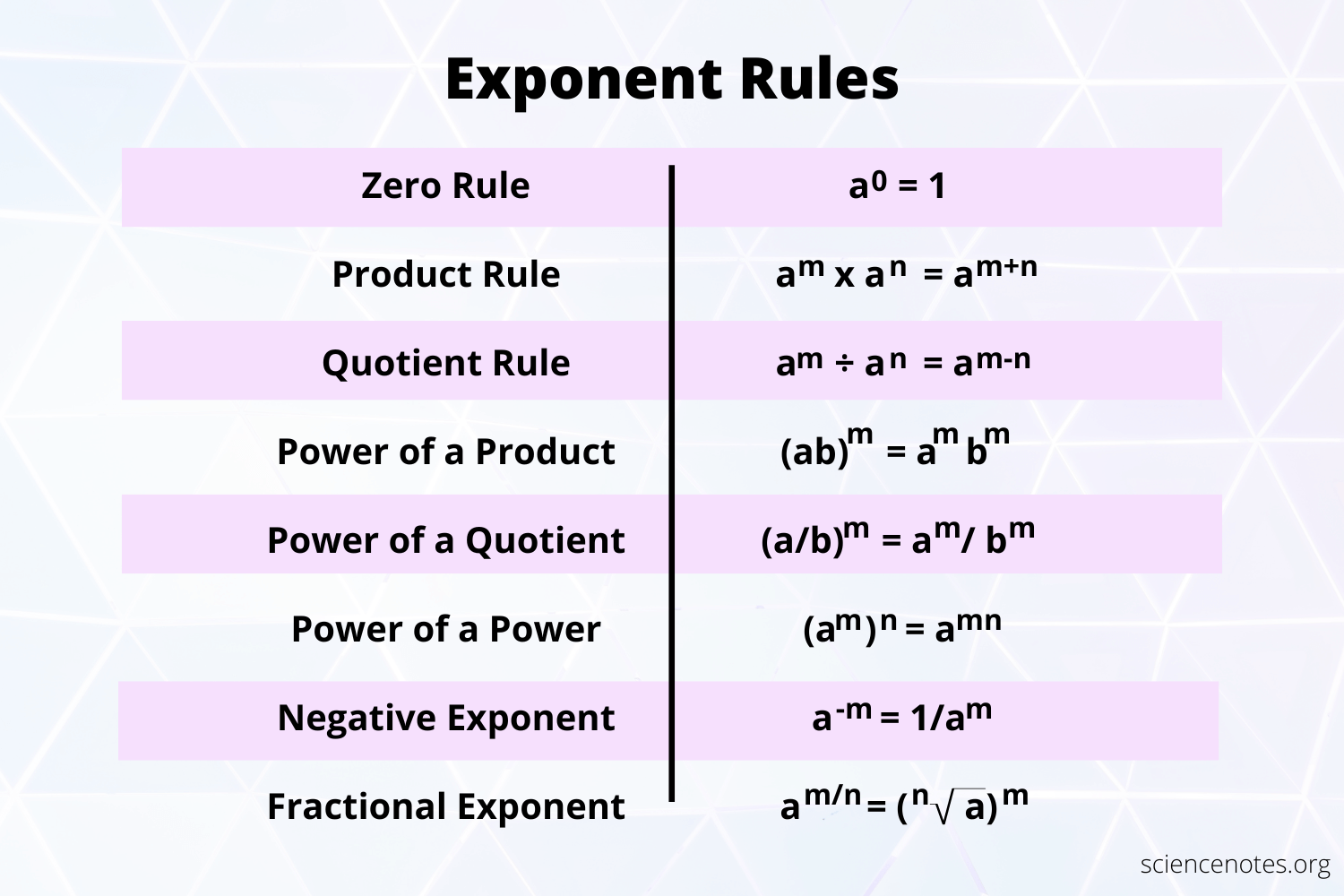
Negative exponents might seem daunting at first, but they’re quite straightforward. Any number raised to a negative exponent (a^{-n}) is equivalent to one over the same number raised to the positive version of that exponent: (\frac{1}{a^n}).
Here’s how it works:
- (x^{-4} = \frac{1}{x^4})
- (3^{-2} = \frac{1}{3^2} = \frac{1}{9})
📝 Note: Remember, fractions with exponents work the same way; for instance, ((\frac{1}{2})^{-3}) equals (2^3 = 8).
Trick #2: Exponent Powering Zero

What happens when you raise any number to the power of 0? Surprisingly, any non-zero number to the 0th power equals 1. This rule stems from the property that any number divided by itself is 1, and when you consider (a^0 = a^{1-1} = \frac{a}{a} = 1), it makes perfect sense.
Trick #3: Fractional Exponents

Fractional exponents are another interesting aspect of exponents, where the numerator indicates the power, and the denominator indicates the root you are taking. So, (a^{m/n} = \sqrt[n]{a^m}). Here’s how you can use this:
- (16^{3⁄2} = \sqrt{16^3} = \sqrt{4096} = 64)
- (25^{1⁄2} = \sqrt{25} = 5)
Trick #4: The Product of Exponents with the Same Base

This is where things get really fun. If you multiply two exponents with the same base, you can add the exponents to simplify the calculation. Let’s see it in action:
| Expression | Simplification |
|---|---|
| (x^3 \times x^2) | (x^{3+2} = x^5) |
| (2^4 \times 2^3) | (2^{4+3} = 2^7 = 128) |

Trick #5: Exponential Equations and Solving
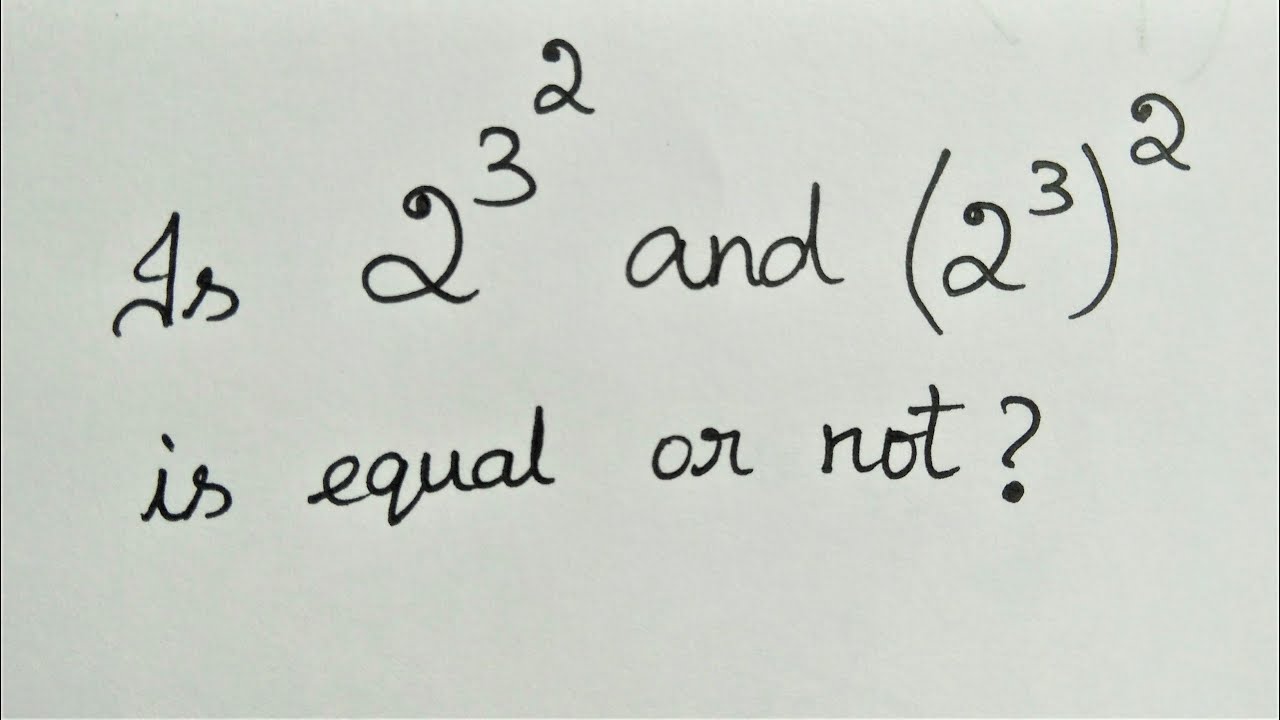
Solving exponential equations can be a brain teaser, but here’s a strategy:
- Use Logarithms: When the bases are the same, taking the logarithm (base 10, natural, or of the same base) of both sides can equalize the exponents.
- Change of Base: If the bases are different, change one to match the other or use a calculator for natural log or common log.
For example, to solve (3^x = 81), since (81 = 3^4), you could set up (x = 4) by using logarithm properties.
In this exploration, we've uncovered the magic behind some of the most practical exponent rules and tricks. These mathematical gems aren't just for solving equations; they're essential for understanding the growth of quantities, the behavior of functions, and can even be seen in natural and financial phenomena. As we wrap up, remember:
- Negative exponents are inverses.
- A number to the 0th power is always 1.
- Fractional exponents combine powers and roots.
- Multiplying or dividing like bases means adding or subtracting exponents, respectively.
- Solving exponential equations often requires logarithms or base changes.
These insights give you not just the tools but a new perspective on how numbers grow and shrink, which is both useful in mathematics and captivating in its beauty.
What is the importance of zero exponents?

+
Understanding that any non-zero number to the power of zero is 1 is crucial for various algebraic operations and functions.
How do you solve exponential equations?

+
Exponential equations are commonly solved by logarithms, allowing you to balance the exponents on both sides of the equation.
What’s the difference between a fractional exponent and a root?

+
A fractional exponent (a^{m/n}) is equivalent to taking the (n)-th root of (a^m). For example, (8^{2⁄3}) is the cube root of (8^2).



