5 Key Tips for Mastering Special Rights Triangles

Embarking on the journey to conquer mathematics often leads us down the path of geometry, where we encounter numerous shapes and formulas. One of the most fundamental concepts within this branch of mathematics is the special right triangle. Mastering these triangles can be a game-changer, not just in solving mathematical problems but also in understanding geometric constructions and proofs. Let's delve into the five key tips that will help you master these intriguing shapes.
1. Understand the Key Types

Firstly, it's crucial to recognize the two primary types of special right triangles: 45°-45°-90° and 30°-60°-90°. Here's a quick overview:
- 45°-45°-90° Triangle: Also known as an isosceles right triangle, where the two legs are equal in length. The ratio of the sides is
1:1:√2. - 30°-60°-90° Triangle: Here, the sides opposite the 30°, 60°, and 90° angles are in the ratio
1:√3:2.
📝 Note: Understanding these ratios helps you solve problems much quicker without resorting to complex calculations.

2. Learn the Formulas by Heart

To quickly master special right triangles, commit the following formulas to memory:
| Triangle Type | Formula |
|---|---|
| 45°-45°-90° | Hypotenuse = Leg × √2 |
| 30°-60°-90° | Short Leg = Hypotenuse ÷ 2 |
| Long Leg = Short Leg × √3 |

By knowing these formulas, you can quickly identify the lengths of sides without complex calculations.
3. Practice with Real-World Applications

Special right triangles appear everywhere, from roof construction to the design of sports fields:
- Roof Trusses: Often constructed using 30°-60°-90° triangles for strength and stability.
- Baseball Diamonds: The infield forms a right triangle with angles that could be related to special triangles if one looks closely.
By practicing with such applications, you cement your understanding and see the relevance of these triangles in real life.
4. Enhance Problem-Solving Skills

To truly master special right triangles, engage in problem-solving activities:
- Start with basic problems that involve finding the length of a side when another is given.
- Gradually move to more complex problems where you need to find the height of an equilateral triangle or the area of a regular hexagon, both related to 30°-60°-90° triangles.
Here's a classic problem to solve:
Your approach would involve:
- Bisecting the triangle into two 30°-60°-90° triangles.
- Using the formula where the hypotenuse is 8 units, so the short leg (height) will be 4 units.
- Then using the area formula for a triangle (Area = 1/2 × base × height).
5. Utilize Visualization
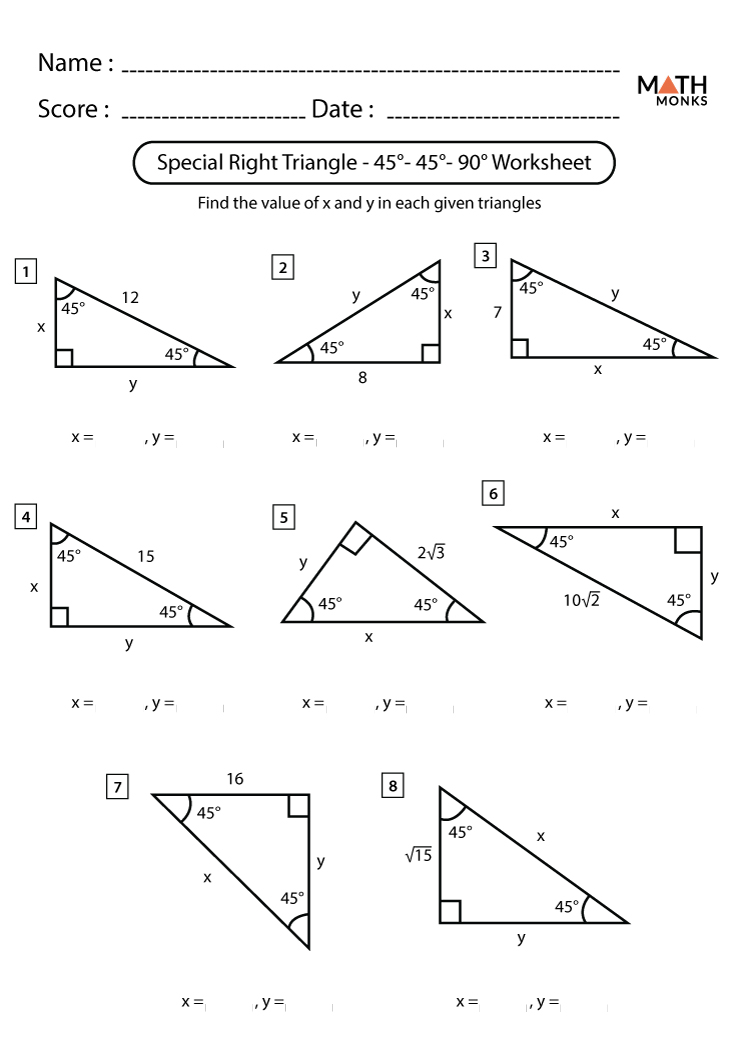
Visualizing these triangles can significantly aid in solving problems:
- Sketch the triangle to see the relationships between the sides visually.
- Use geometric construction tools like compasses and straightedges to draw and measure special right triangles.

Final Insights
To master special right triangles, one must embrace their simplicity and the power they offer in problem-solving. By understanding the key types, memorizing formulas, applying them to real-life scenarios, enhancing problem-solving skills, and visualizing the triangles, you gain a robust foundation in geometry. These tips not only prepare you for complex geometric problems but also provide a stepping stone towards mastering other mathematical concepts.
Why are special right triangles so important in geometry?

+
Special right triangles have fixed ratios between their sides, making them invaluable for quick calculations in geometry and trigonometry, simplifying problem-solving in various fields.
Can these formulas be applied to any triangle?

+
These formulas are specific to special right triangles (45°-45°-90° and 30°-60°-90°), and while other triangles might have similar properties, these formulas aren’t universally applicable.
What’s the best way to memorize these formulas?

+
Regular practice, creating mnemonics, and associating the formulas with visual representations of the triangles are effective ways to remember these formulas.
Related Terms:
- Special Right Triangles Worksheet
- Special rights triangles worksheet pdf
- Special Triangles Worksheet pdf
- Special Right Triangles PDF
- special right triangles worksheet 45 45 90