Graphing Mastery: Intercept Worksheet Guide

Graphing equations is a fundamental skill in algebra, and understanding how to identify intercepts plays a pivotal role in both graphing and solving equations. Intercepts, or points where the graph touches the x-axis or y-axis, are crucial for visualizing linear functions, quadratic equations, and beyond. In this guide, we'll dive deep into the process of working with intercepts through worksheets, providing you with a comprehensive toolkit to master this aspect of mathematics.
Understanding Intercepts

Before we tackle worksheets, let’s clarify what intercepts are:
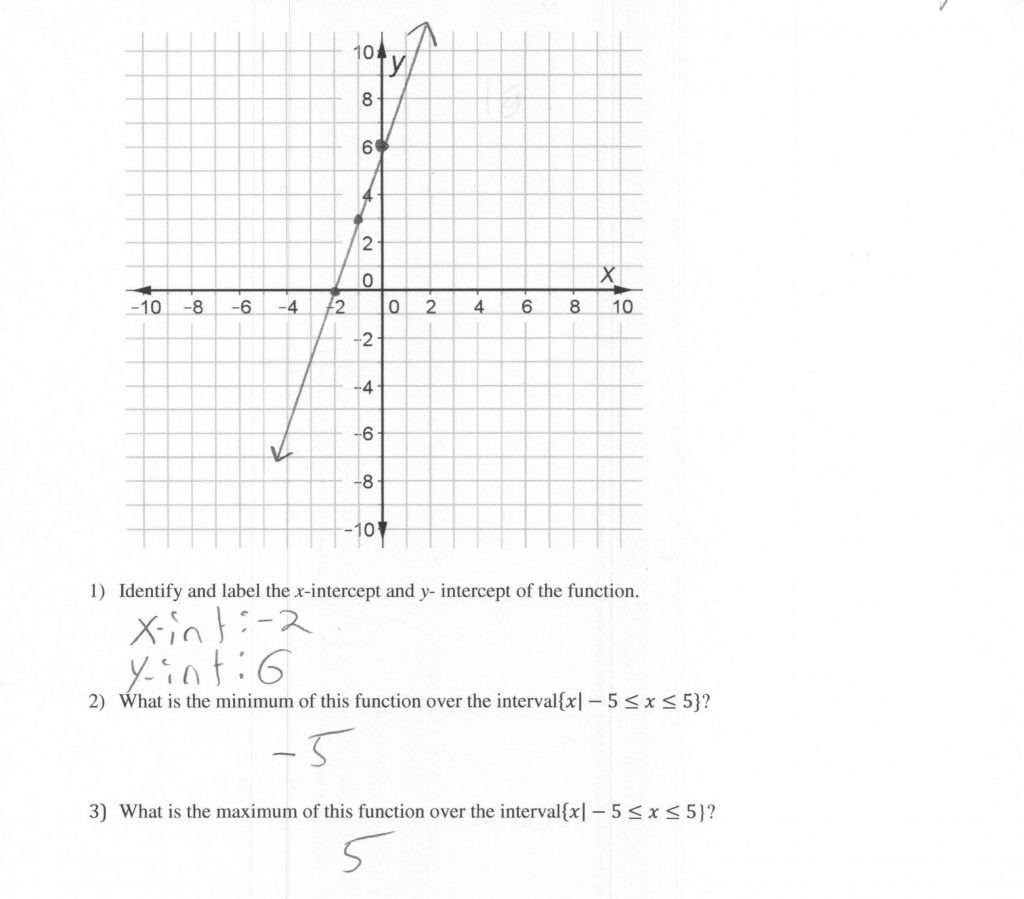
- X-Intercept: The point where the graph crosses or touches the x-axis. At this point, the y-coordinate is 0.
- Y-Intercept: The point where the graph crosses or touches the y-axis. Here, the x-coordinate is 0.
📌 Note: Intercepts are critical because they give us immediate insight into where a line or curve begins or ends on a coordinate plane.
Finding Intercepts

To find intercepts:
- X-Intercept: Set y = 0 and solve for x. This gives you the point (x, 0).
- Y-Intercept: Set x = 0 and solve for y. This gives you the point (0, y).
Example:
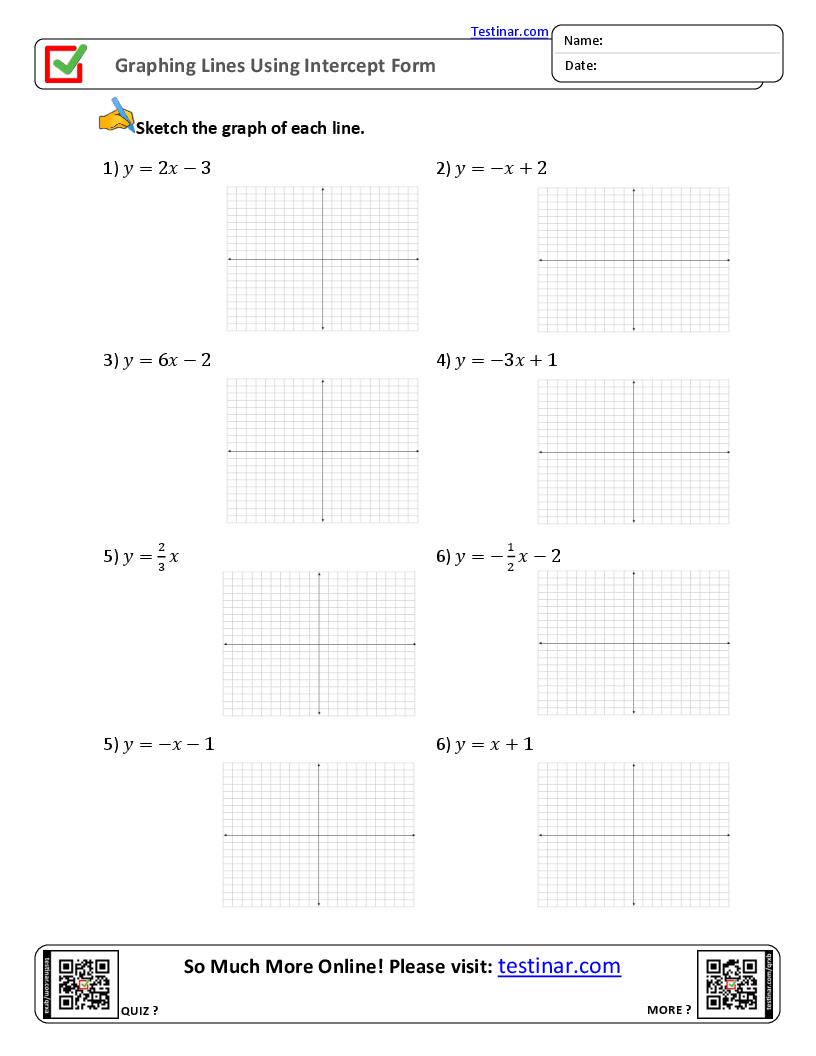
Consider the linear equation ( y = 2x + 3 ):
- X-Intercept: Set y to 0. ( 0 = 2x + 3 ). Solving this gives ( x = -1.5 ), so the x-intercept is (-1.5, 0).
- Y-Intercept: Set x to 0. ( y = 2(0) + 3 ), which simplifies to y = 3, so the y-intercept is (0, 3).
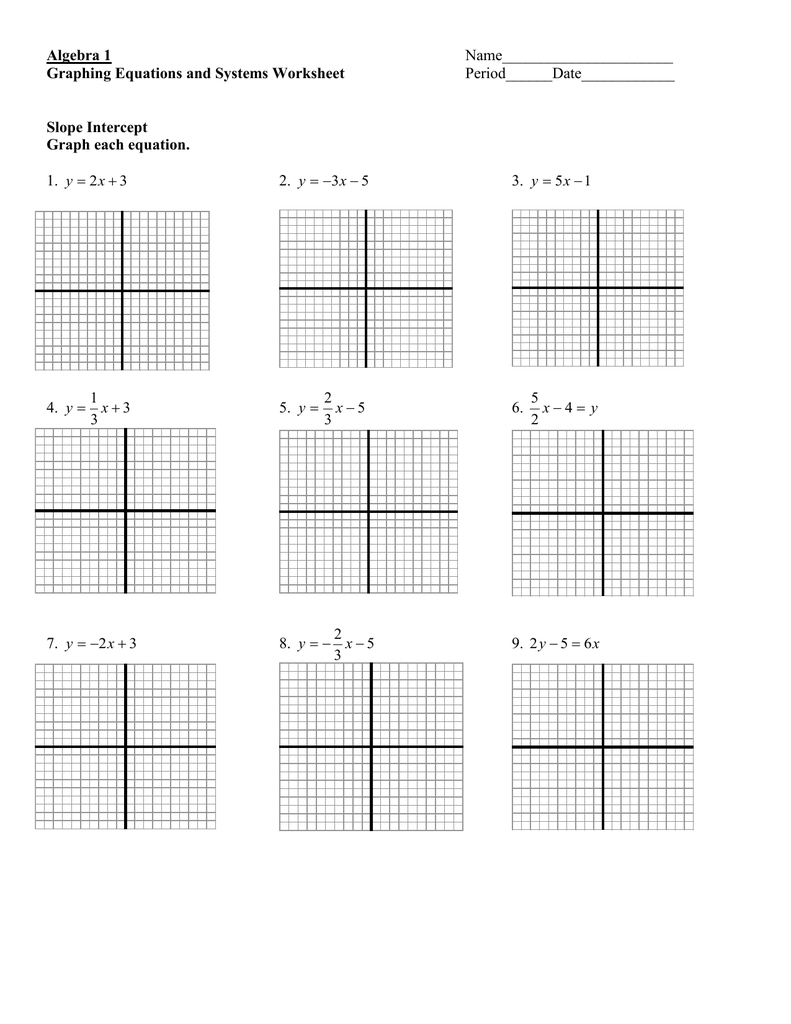
Using Worksheets for Practice

Here’s how you can utilize worksheets to enhance your understanding:
- Identify Intercepts: Worksheets will provide equations for which you need to find both x and y intercepts.
- Graphing: After finding intercepts, plot these points and sketch the line or curve.
- Verifying: Check your work by using intercept points to confirm the graph matches the equation.
Steps for Working with Intercept Worksheets
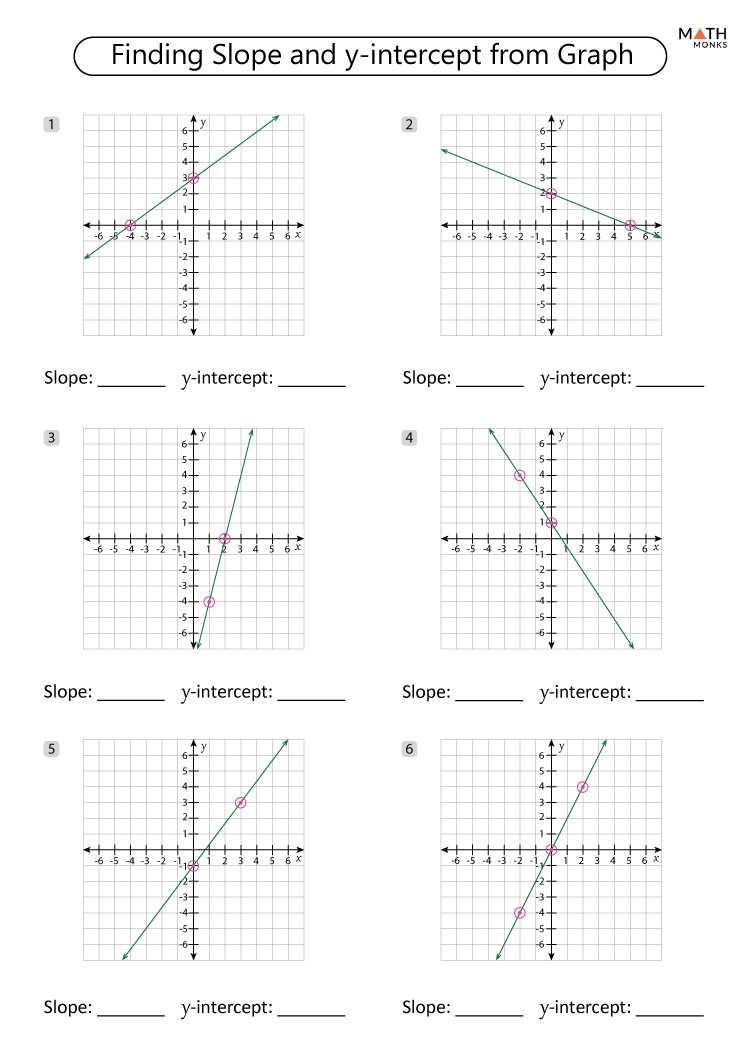
- Read the Equation: Begin with the given equation on the worksheet.
- Find X-Intercept: Set y to 0 and solve for x. Record the result.
- Find Y-Intercept: Set x to 0 and solve for y. Record this point as well.
- Graph the Points: Use graph paper or a graphing calculator to plot the intercepts. Draw a straight line through these points for linear equations or sketch the curve for higher degree equations.
- Verify: Substitute the intercepts back into the original equation to ensure they satisfy it.
📌 Note: For quadratic equations, there can be up to two x-intercepts, but there is always one y-intercept.
Common Mistakes to Avoid
- Not setting one variable to zero when finding intercepts.
- Failing to solve equations completely or incorrectly.
- Plotting the intercepts on the wrong axes.
- Misinterpreting fractional or negative intercepts.
Advanced Techniques

For more complex equations, here are some techniques:
- Vertex Form: For quadratic equations in vertex form, the y-intercept can often be determined immediately, and x-intercepts can be found using the vertex and symmetry.
- Slope-Intercept Form: For linear equations ( y = mx + b ), the y-intercept is b, and you can use the slope to find another point.
Application to Real-Life Problems

Intercepts are not just theoretical; they have practical applications:
- Business: The y-intercept can represent the initial cost or fixed expenses in a profit equation.
- Physics: In physics, intercepts can indicate starting conditions or inherent properties in equations of motion or energy.
- Economics: Intercepts help in understanding supply and demand curves where the x-intercept might represent a price where quantity demanded becomes zero.
After exploring these concepts through worksheets, you'll find yourself better equipped to handle graphing, algebra, and even calculus problems where intercepts play a pivotal role. This guide has provided you with the theoretical background, practical steps, and real-world applications of intercepts, turning you into a graphing master.
Why are intercepts important in graphing?
+
Intercepts provide essential reference points for graphing equations. They simplify the process of plotting curves or lines by offering anchor points, which help in visualizing the behavior of the function.
Can you graph a line with only one intercept?

+
With just one intercept, you can’t graph a line accurately. You need at least two points or additional information like the slope to determine the line’s path on the graph.
How do intercepts change with transformation of functions?

+
Transformations of functions like shifting or scaling can alter intercepts:
- Vertical shifts change the y-intercept but not the x-intercept.
- Horizontal shifts change the x-intercept but not the y-intercept.
- Scaling can affect both intercepts depending on the direction of the scale.


