Quadratic Functions Graphing Worksheet: Master the Basics

Exploring the Essentials of Quadratic Functions

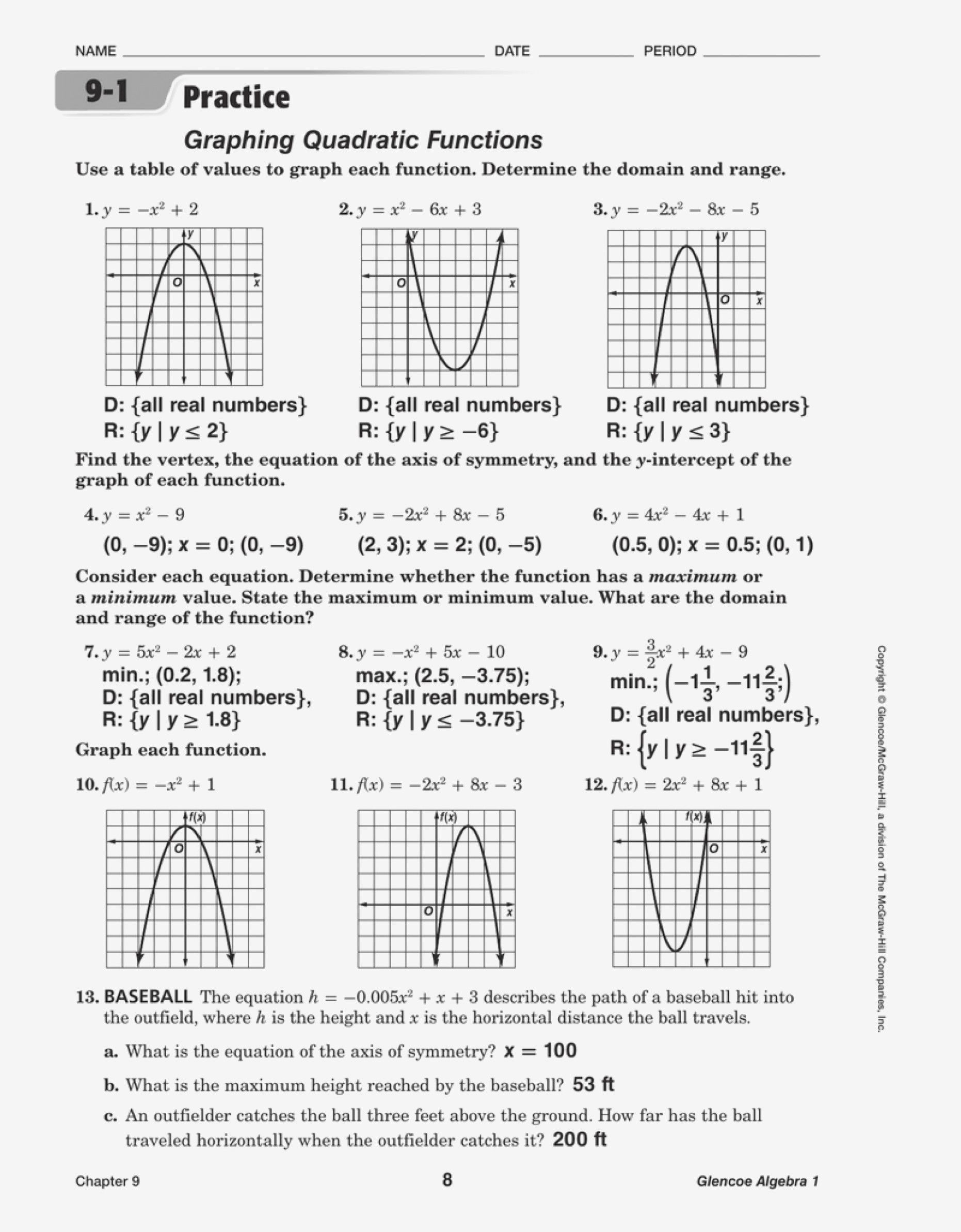
Quadratic functions are fundamental in algebra, and mastering their graphing can significantly enhance your understanding of mathematics. These functions, expressed in the form f(x) = ax² + bx + c, where a, b, and c are constants, exhibit a parabolic shape when graphed. This shape is crucial for various applications in fields like physics, engineering, and finance. In this comprehensive guide, we'll delve into the essentials of graphing quadratic functions, ensuring you grasp the basics and build a solid foundation for more advanced topics.

Understanding the Standard Form

The standard form of a quadratic function, f(x) = ax² + bx + c, is the starting point for our exploration:

• a determines the direction and width of the parabola:
  • If a > 0, the parabola opens upwards.
  • If a < 0, the parabola opens downwards.
  • The value of |a| dictates how narrow or wide the parabola is. A larger |a| means a narrower parabola.
• b influences the x-coordinate of the vertex.
• c is the y-intercept, where the parabola intersects the y-axis.

Graphing Techniques

Identify Key Points

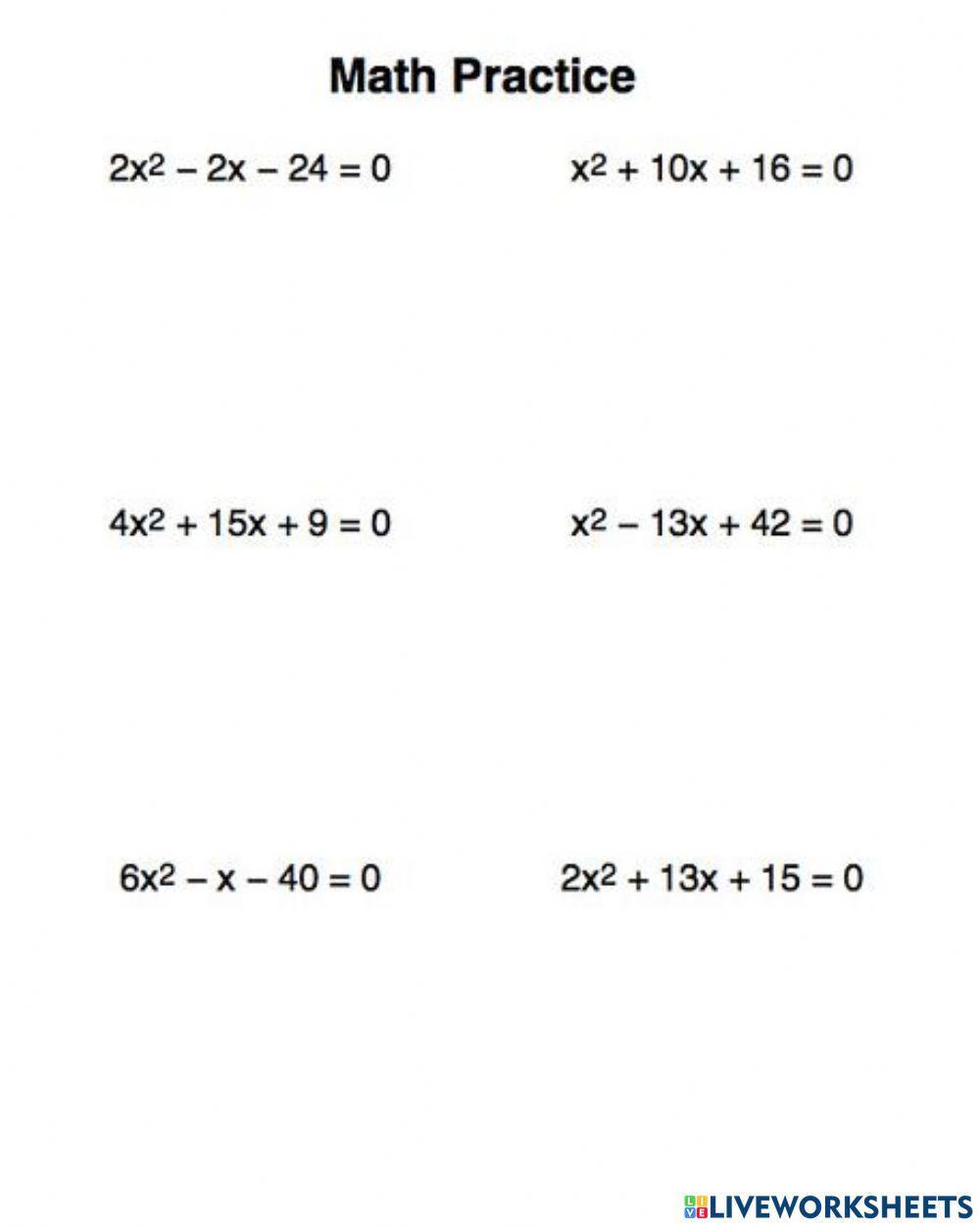
Before plotting, identifying crucial points helps in sketching the parabola:

• The vertex, or the turning point of the parabola, is found using the formula x = -b / 2a.
• The y-intercept occurs at c when x is 0.
• The x-intercepts (roots or zeros) are found by solving ax² + bx + c = 0. This can be done using factorization, the quadratic formula, or completing the square.

Vertex Form

For more direct graphing, we can use the vertex form of a quadratic function: f(x) = a(x-h)² + k:

• (h, k) is the vertex of the parabola.
• The value of a still influences the parabola’s width and direction.

Step-by-Step Graphing

To graph a quadratic function:

1. Identify the direction and width using the value of a.
2. Find the vertex using the formula x = -b / 2a and calculate the corresponding y-value.
3. Locate the y-intercept by evaluating f(0), which equals c.
4. Determine x-intercepts by solving ax² + bx + c = 0, if applicable.
5. Sketch the parabola using the vertex, y-intercept, and x-intercepts as guide points. Remember to extend the curve beyond these points, following the parabolic path.

🌟 Note: Symmetry is a key property of parabolas. The vertex lies at the midpoint between the x-intercepts (if they exist), making the graph symmetrical about the vertical line through the vertex.

Exploring with Examples

To solidify our understanding, let’s look at some examples:

Example 1: Graphing f(x) = x² + 4x + 3

• a = 1, b = 4, c = 3. The parabola opens upwards since a > 0.
• The vertex is at x = -4 / 2(1) = -2. Substituting back, we find y = (-2)² + 4(-2) + 3 = -1. The vertex is at (-2, -1).
• The y-intercept is 3 (c = 3).
• To find x-intercepts, solve x² + 4x + 3 = 0, which can be factored into (x+1)(x+3) = 0. Thus, x-intercepts are -1 and -3.
• Sketch the parabola, with vertex (-2, -1) and through x-intercepts at (-1, 0) and (-3, 0), and y-intercept at (0, 3).

Example 2: Converting to Vertex Form

Consider f(x) = -2x² + 8x - 3:

• We can convert this to vertex form by completing the square or using the vertex formula:
  • Vertex: x = -8 / 2(-2) = 2. Substituting back, we find y = -2(2)² + 8(2) - 3 = -2.
  • So, the vertex form is f(x) = -2(x-2)² - 2, indicating the parabola opens downwards and is narrower than the standard parabola.

These examples illustrate how changing parameters affects the graph, helping in visualizing and sketching parabolas efficiently.

🌐 Note: Online graphing tools can be invaluable for visualizing quadratic functions and confirming your work, especially when you're new to graphing these equations.

Final Thoughts

Graphing quadratic functions goes beyond plotting a simple curve; it’s about understanding the interplay between their algebraic forms and geometric interpretations. Each parameter in the quadratic equation influences the graph’s shape, size, and orientation, providing a rich area of study that connects algebra to the visual world of geometry.

By mastering these basics, you're not only preparing for more complex polynomial and trigonometric functions but also equipping yourself with essential tools for problem-solving in real-world scenarios. Whether it's calculating the maximum height of a projectile or optimizing a financial model, the principles of quadratic functions are integral. Keep practicing, and soon, these curves will become second nature, enabling you to explore and solve problems with confidence and ease.

What does the ‘a’ parameter in f(x) = ax² + bx + c represent?

+

The ‘a’ parameter dictates the direction the parabola opens and its width. If a > 0, the parabola opens upwards; if a < 0, it opens downwards. Additionally, the larger the absolute value of ‘a’, the narrower the parabola.

Can a quadratic function have no x-intercepts?

+

Yes, when the parabola’s vertex is above or below the x-axis and the parabola opens in a direction that does not cross the x-axis (i.e., the discriminant, b²-4ac, is less than zero).

How do you find the vertex from the standard form of a quadratic function?

+

The x-coordinate of the vertex is given by x = -b / (2a). Substitute this x-value back into the function to find the y-coordinate, forming the vertex (x, f(x)).