5 Essential Gas Law Calculations for Chemistry Success

The study of gas laws in chemistry provides a foundation for understanding the behavior of gases under various conditions. These laws, derived through experiments, help in predicting how gases will behave in different scenarios, which is crucial for numerous applications in chemical engineering, meteorology, and industrial processes. Here are five essential gas law calculations that every student should master to achieve success in chemistry:
Boyle's Law: Pressure-Volume Relationship

Boyle's Law, discovered by Robert Boyle in the 17th century, describes the inverse relationship between the pressure and volume of a gas when temperature is held constant. The equation for Boyle's Law is:
[ P_1 \times V_1 = P_2 \times V_2 ]
- P stands for Pressure
- V stands for Volume
- Subscripts 1 and 2 denote the initial and final states
Example: If the pressure of a gas at 101.3 kPa decreases to 50.65 kPa, and its initial volume is 2 L, what will be its final volume?
Using Boyle's Law formula:
[ 101.3 \times 2 = 50.65 \times V_2 ]
[ V_2 = \frac{101.3 \times 2}{50.65} = 4 \text{ L} ]
🔍 Note: It's crucial to ensure the units of pressure and volume are consistent when applying Boyle's Law.
Charles' Law: Temperature-Volume Relationship

Charles' Law states that the volume of a gas increases with increasing temperature, provided the pressure remains constant. The equation is:
[ \frac{V_1}{T_1} = \frac{V_2}{T_2} ]
- V stands for Volume
- T stands for Absolute temperature (in Kelvin)
Example: A balloon's volume at 273 K is 1 L. What will be its volume if the temperature is doubled?
[ \frac{1}{273} = \frac{V_2}{546} ]
[ V_2 = \frac{1 \times 546}{273} = 2 \text{ L} ]
🔎 Note: Remember that temperature must be in Kelvin when using Charles' Law.
Gay-Lussac's Law: Pressure-Temperature Relationship
Gay-Lussac's Law relates the pressure of a gas to its temperature at constant volume. The equation is:
[ \frac{P_1}{T_1} = \frac{P_2}{T_2} ]
- P stands for Pressure
- T stands for Absolute temperature (in Kelvin)
Example: A gas at 100 kPa and 300 K is heated to 600 K. What will be the new pressure?
[ \frac{100}{300} = \frac{P_2}{600} ]
[ P_2 = \frac{100 \times 600}{300} = 200 \text{ kPa} ]
Avogadro's Law: Moles-Volume Relationship

Avogadro's Law states that equal volumes of all gases at the same temperature and pressure contain the same number of molecules. This relationship is expressed as:
[ \frac{V_1}{n_1} = \frac{V_2}{n_2} ]
- V stands for Volume
- n stands for Number of moles
Example: If 2 moles of gas occupy 44.8 L at STP, how many moles are present if the volume is reduced to 22.4 L?
[ \frac{44.8}{2} = \frac{22.4}{n_2} ]
[ n_2 = \frac{2 \times 22.4}{44.8} = 1 \text{ mole} ]
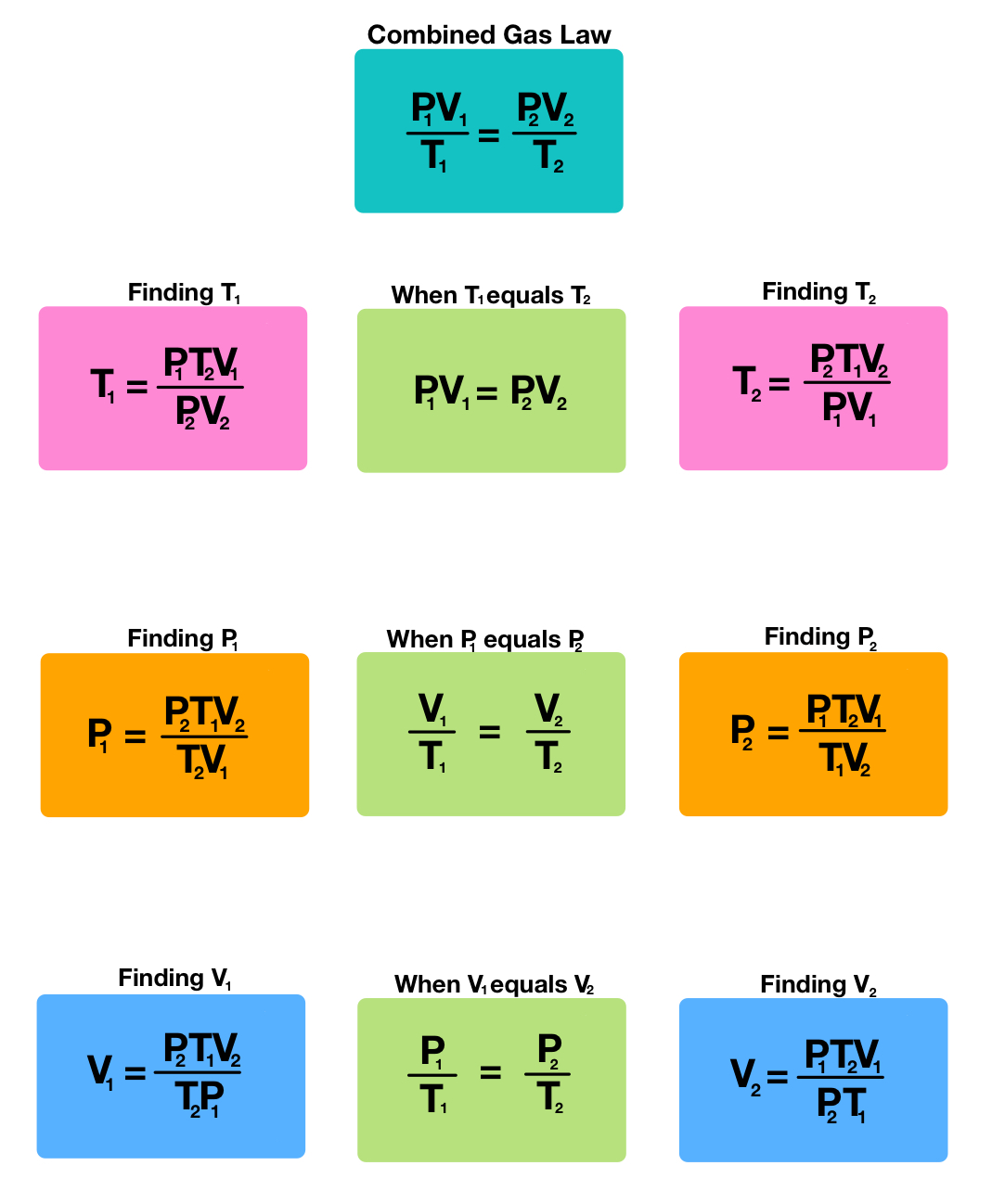
Combined Gas Law: Combining Boyle's, Charles', and Gay-Lussac's Laws

The Combined Gas Law incorporates the relationships from Boyle's, Charles', and Gay-Lussac's laws to cover changes in pressure, volume, and temperature. The equation is:
[ \frac{P_1 \times V_1}{T_1} = \frac{P_2 \times V_2}{T_2} ]
Example: A gas at 1 atm, 25 L, and 300 K is compressed to 15 L and the temperature increases to 350 K. What is the final pressure?
[ \frac{1 \times 25}{300} = \frac{P_2 \times 15}{350} ]
[ P_2 = \frac{1 \times 25 \times 350}{300 \times 15} = 1.833 \text{ atm} ]
The mastery of these gas laws is not just about performing calculations; it's about understanding how gases behave in various conditions. From simple experiments in a lab to complex industrial processes, the principles derived from these laws are invaluable. Here are a few points to keep in mind:
- Consistency of Units: Ensure that your units for pressure, volume, and temperature are consistent in your calculations.
- Use of Absolute Temperature: Temperature must be in Kelvin for these calculations since gas laws apply only to ideal gases, which have no inherent zero volume or pressure.
- Application Beyond Chemistry: Gas laws are not confined to chemistry; they are used in engineering, especially in fields like thermodynamics and fluid mechanics.
By grasping these fundamental gas laws, students not only excel in their examinations but also prepare themselves for real-world applications where understanding gas behavior is crucial. The ability to predict how changes in one property of a gas affect the others is a cornerstone of chemical science. Whether you're a future chemist, engineer, or simply someone interested in the physical world, these principles provide a framework for understanding the invisible yet profoundly impactful nature of gases.
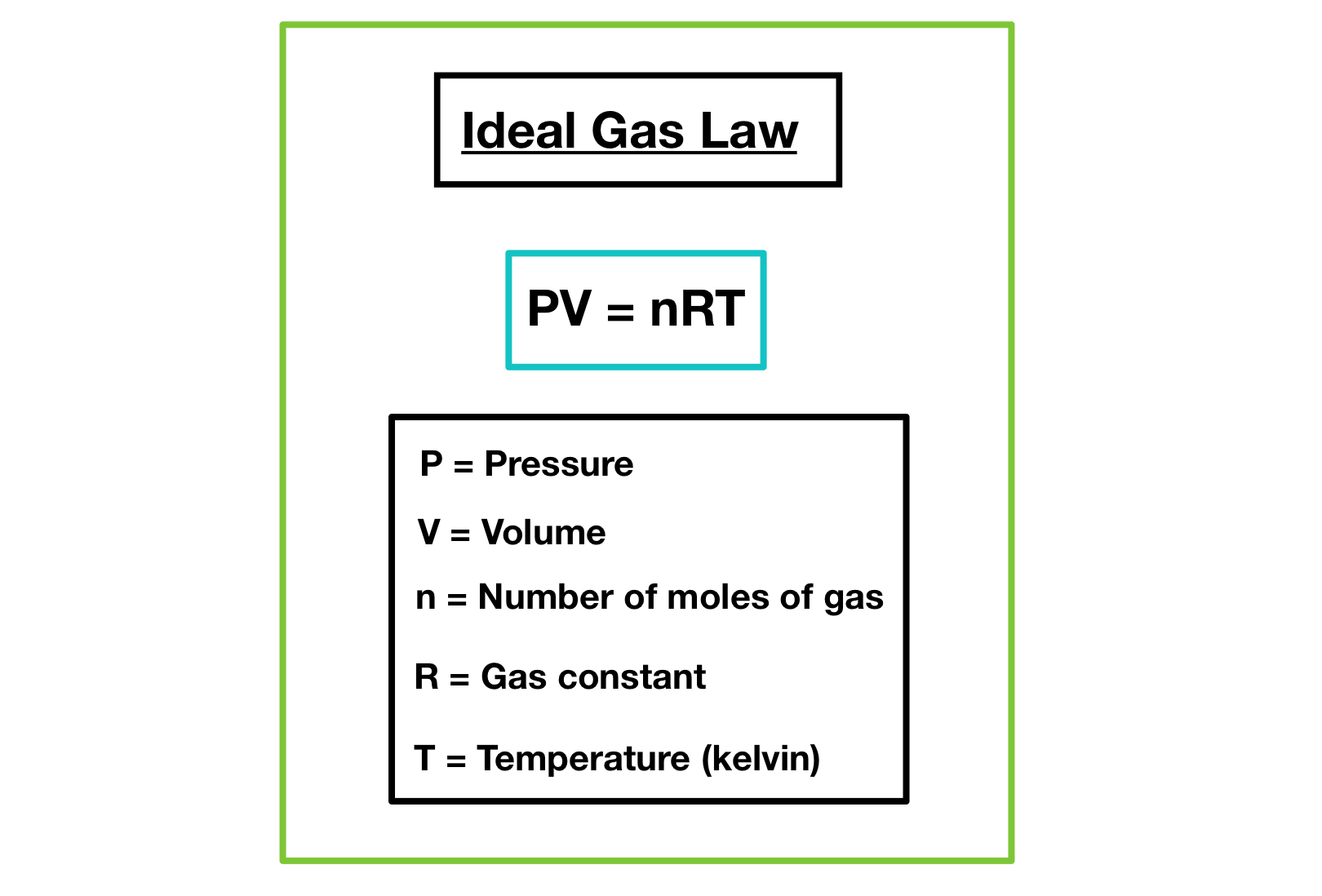
What if I need to calculate the mass of a gas?
+
To calculate the mass of a gas, use the ideal gas law PV = nRT. Here, n (number of moles) can be converted to mass using the molecular weight of the gas.
Can these laws be applied to real gases?

+
Yes, but with limitations. Real gases deviate from ideal behavior under conditions of high pressure and low temperature, and corrections must be made using equations like van der Waals equation.
What are the common units for gas law calculations?

+
Common units include:
- Pressure (P): Atmospheres (atm), kilopascals (kPa), mmHg
- Volume (V): Liters (L), cubic meters (m³)
- Temperature (T): Kelvin (K)
- Amount of substance (n): Moles (mol)


