Factoring Quadratic Trinomials Worksheet - Simplify Your Math Skills

Factoring quadratic trinomials, often referred to as factoring quadratics, is a fundamental skill in algebra that can significantly enhance your mathematical prowess. This technique is not just about solving equations; it's a gateway to understanding more complex polynomial expressions and equations, which are prevalent in higher mathematics. In this blog, we will guide you through the process of factoring quadratic trinomials, offering insights, tips, and practical examples to boost your algebra skills.

The Basics of Quadratic Trinomials

At its core, a quadratic trinomial is an expression of the form ax² + bx + c, where a, b, and c are constants, and a ≠ 0. Here’s what you need to know:

• Form: ax² + bx + c
• Examples: 2x² + 7x - 4, x² + 4x + 4
• Purpose: To find two binomials whose product results in the given trinomial.

When factoring, the goal is to rewrite the trinomial in terms of factors, usually binomials:

• (dx + e)(fx + g) where d * f = a and e * g = c

🔑 Note: While d and f multiply to give a, e and g give c. Moreover, d * g + e * f should equal b in the trinomial.

Steps for Factoring Quadratic Trinomials

Here is a step-by-step guide to help you through the process:

1. Identify a, b, and c

   
   

   Consider the trinomial ax² + bx + c. Here, a is the coefficient of x², b is the coefficient of x, and c is the constant term.

2. Find Two Numbers

   
   

   Look for two numbers whose product is a * c and whose sum is b. This step is crucial for splitting the middle term.

   • If a is 1, this step simplifies to finding factors of c.
   • For a not equal to 1, use trial and error or the AC method.

3. Rewrite the Middle Term

   
   

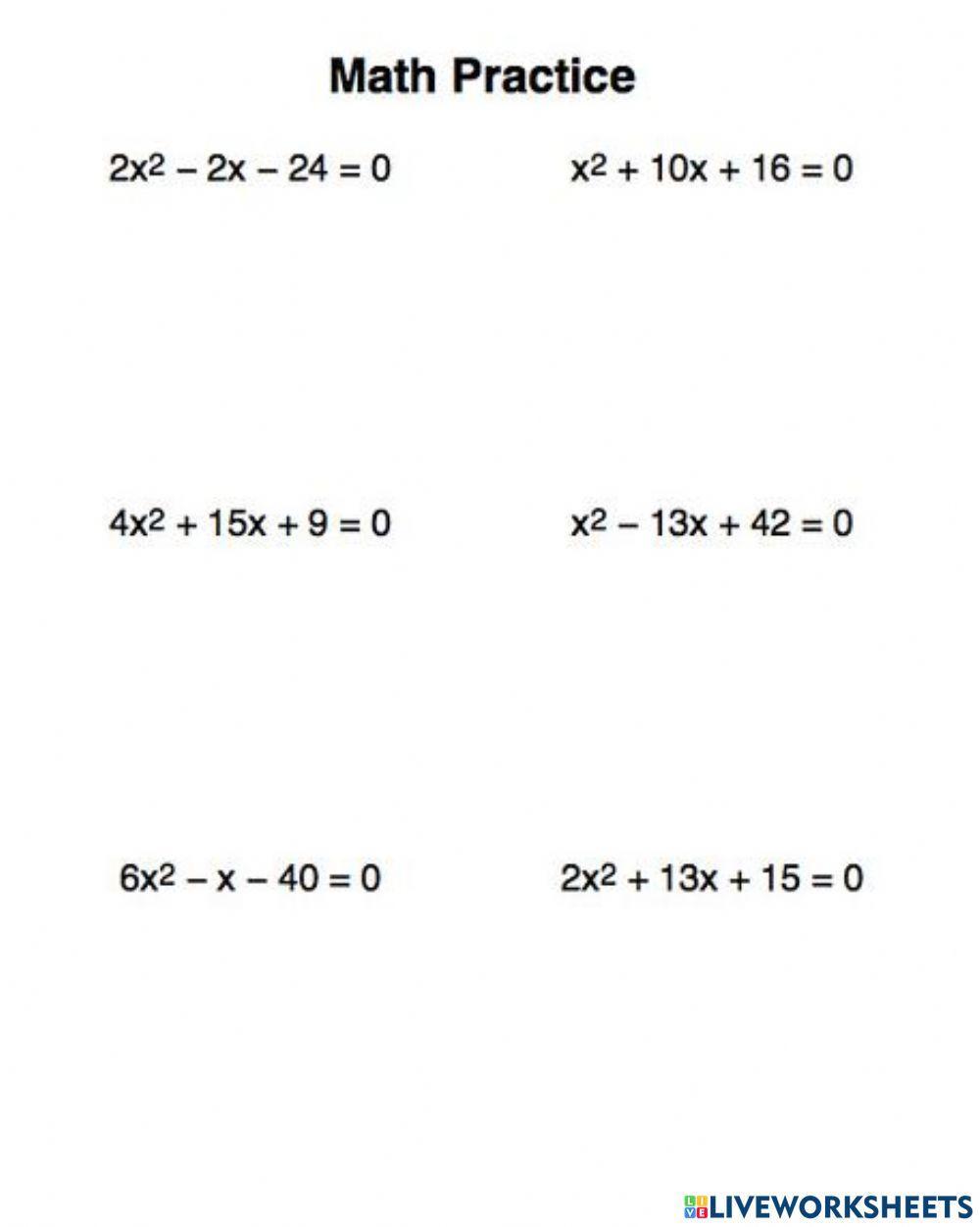
   Replace bx with the sum of these two numbers. For example, if a * c is 15, and b is 8, we could split bx as 5x + 3x (because 5 * 3 = 15 and 5 + 3 = 8).

4. Group Terms

   
   

   Group the terms in pairs. For instance, if you rewrote the trinomial as ax² + 5x + 3x + c, you would group ax² + 5x and 3x + c.

5. Factor Out Common Factors

   
   

   Factor out the common factor from each group. The previous example might look like this: x(az + 5) + 3(z + 1).

6. Combine and Solve

   
   

   Factor out the common binomial from the grouped terms, and you will have the factored form of the quadratic trinomial.

Examples to Illustrate Factoring

Here are a few examples to help you grasp the concept:

• Example 1: x² + 7x + 10
  • Factors: (x + 2)(x + 5)
  • Explanation: (2 * 5 = 10 and 2 + 5 = 7)
• Example 2: 2x² + 5x - 3
  • Factors: (2x - 1)(x + 3)
  • Explanation: (2 * 3 = 6 and -1 * -3 = 3, and 5 = 3 - 2)
• Example 3: 6x² - 13x + 6
  • Factors: (3x - 2)(2x - 3)
  • Explanation: (3 * 2 = 6, -2 * -3 = 6, and 13 = 6 + 7)

Common Mistakes to Avoid

Here are some common pitfalls to watch out for:

• Ignoring the Sign: The signs of the factors are crucial. Ensure you account for positive and negative values.
• Miscalculating Coefficients: Double-check your arithmetic, especially when dealing with the product and sum of numbers.
• Overcomplicating the Process: Sometimes, the simplest approach is the best. Look for prime factors or use the AC method if possible.
• Failing to Group: Grouping is key. If you miss this step, you’ll miss the opportunity to factor out common terms.

⚠️ Note: If a quadratic trinomial does not appear to factor, it might be prime, meaning it cannot be factored further over the integers.

In summary, factoring quadratic trinomials is an essential skill for algebra, opening doors to solving equations, simplifying expressions, and understanding deeper mathematical concepts. By following the outlined steps, being mindful of common errors, and practicing with various examples, you'll find that factoring becomes second nature. Remember, like any skill, it requires practice, patience, and a keen eye for patterns and numbers.

Why is factoring important in algebra?

+

Factoring helps in solving polynomial equations, simplifying expressions, and understanding the structure of algebraic expressions. It’s crucial for further mathematical concepts like calculus and beyond.

What are the common signs that a quadratic trinomial is factorable?

+

If you can find two numbers whose product is ac and whose sum is b, then the trinomial is likely factorable. Also, if the discriminant (b² - 4ac) is a perfect square, it’s another sign the trinomial can be factored.

Can all quadratic trinomials be factored?

+

No, not all quadratic trinomials can be factored with integer coefficients. Some are prime over integers, meaning they cannot be expressed as a product of two binomials with integer coefficients.

How do you handle negative coefficients?

+

When dealing with negative coefficients, remember to account for the signs. If b is negative, one of the numbers found in step 2 should be negative, and their sum should equal the negative value of b.

Are there techniques for factoring more complex trinomials?

+

Yes, techniques like the quadratic formula, synthetic division, or completing the square can be used for more complex polynomials or when factoring by grouping fails.