Master Exponential Equations with This Engaging Worksheet!

Exponential equations are fundamental in a variety of fields from biology to finance, making their mastery not only an academic endeavor but also a tool for practical real-world applications. Whether you're a student grappling with these equations or a professional requiring quick solutions, our interactive worksheet will guide you through the complexities and thrills of solving exponential equations efficiently.
Understanding Exponential Equations

To excel in solving exponential equations, we must first understand what they are and how they function:
- Exponential Equations are of the form a^x = b, where ‘a’ is the base and ‘x’ is the exponent. The challenge is to solve for ‘x’.
- They differ from linear equations where the variable is not an exponent but part of the base or within a linear term.
Key Properties of Exponents

Before diving into the specifics of solving these equations, here are some important properties of exponents to keep in mind:
- a^m * a^n = a^(m+n)
- (a^m)^n = a^(mn)
- (ab)^m = a^m * b^m
- a^0 = 1 for any ‘a’ other than 0
The Basics of Solving Exponential Equations

The core strategy for solving exponential equations includes:
- Take the Logarithm: When the bases on both sides of the equation are not the same, use logarithms to solve. Either common log (log base 10) or natural log (log base e) can be employed.
- Exponentiate Both Sides: If you can easily make the bases the same, then you can solve by exponentiating both sides to the power necessary to remove the exponent from ‘x’.
Step-by-Step Solution Process

Let’s explore how to solve the equation 2^x = 8:
- Take the Logarithm: Log both sides log(2^x) = log(8).
- Use Log Properties: x * log(2) = log(8)
- Solve for x: Divide both sides by log(2) to get x = log(8) / log(2).
🌟 Note: Remember, logarithms can help transform multiplication into addition, making complex exponential equations manageable.
Solving Exponential Equations with Different Bases

When the bases differ, you can still use logarithms to find the solution. Here’s an example:
- Solve the equation 3^x = 9 by recognizing that 9 = 3^2.
Or you could use logarithms:
- Log both sides: log(3^x) = log(9).
- Use log properties: x * log(3) = log(9).
- Solve for x: x = log(9) / log(3).
Using a Calculator

In practical scenarios, solving exponential equations often requires the use of a scientific or graphing calculator to handle logarithms:
- Find log(3) and log(9) using the calculator.
- Perform the division to get the value of x.
Advanced Techniques and Complex Cases

When equations become more complex, understanding advanced techniques can be a game-changer:
- Change of Base Formula: If your calculator does not have a log function for a particular base, use log_a(b) = log_c(b) / log_c(a).
- Exponential Functions: Often in applications like growth or decay models, understanding the context can simplify solving.
| Equation | Approach |
|---|---|
| 2^x = 64 | Recognize that 64 = 2^6, or use log properties. |
| e^x = 5 | Take the natural log of both sides: ln(e^x) = ln(5) = x * ln(e) = x * 1 = x. |
| 10^x = 0.1 | Use log properties or recognize that 10^-1 = 0.1. |

Applications of Exponential Equations
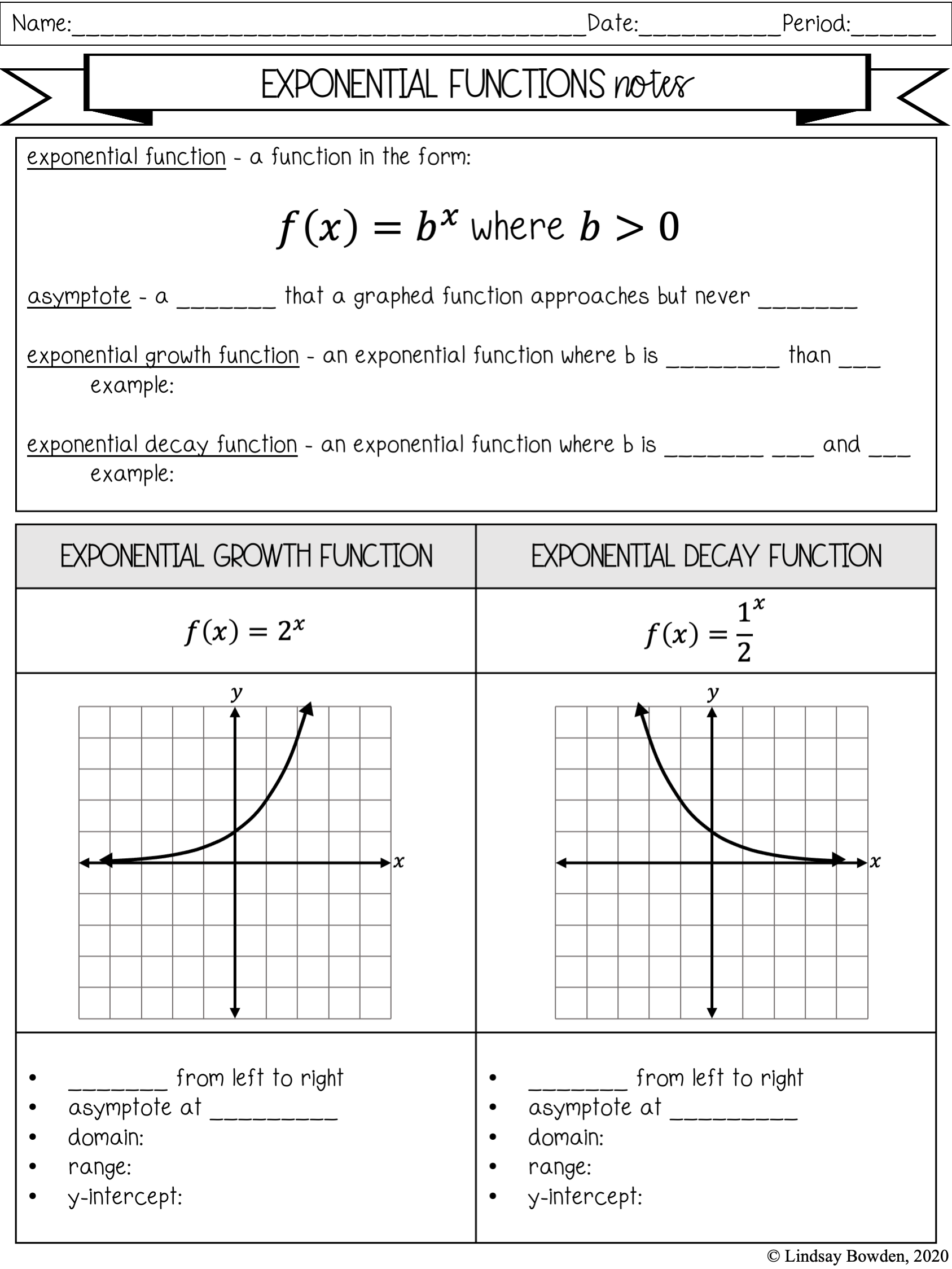
Exponential equations are not just theoretical constructs; they have practical applications:
- Compound Interest: The formula A = P(1 + r/n)^(nt), where ‘A’ is the amount of money accumulated after ’t’ years, ‘P’ is the principal amount, ‘r’ is the annual interest rate, ‘n’ is the number of times that interest is compounded per year, and ’t’ is the time the money is invested or borrowed for.
- Population Growth: Exponential growth or decay models for population studies where N = N_0 * e^(kt), ‘N’ being the final number of people, ‘N_0’ the initial population, ‘k’ the growth or decay constant, and ’t’ the time frame.
💡 Note: Understanding the context behind an exponential equation can simplify the solution process.
In closing, mastering exponential equations opens up a world of mathematical and real-world problem-solving. From financial calculations to understanding population dynamics, the skills you've learned here are invaluable. By employing logarithms, understanding exponent properties, and recognizing the practical applications, you can confidently tackle and solve any exponential equation that comes your way. The process, while initially challenging, becomes second nature with practice, enabling you to see the beauty and efficiency of exponential math.
What is the easiest way to solve an exponential equation?

+
The simplest method often involves making the bases the same and using the properties of exponents. When this is not feasible, employing logarithms is the standard approach.
Why do we use logarithms to solve exponential equations?

+
Logarithms convert multiplicative operations into additive ones, simplifying complex exponential problems. By taking the logarithm of both sides, the exponent can be brought down as a coefficient.
What’s the importance of understanding exponential growth or decay in real life?

+
Understanding these models is crucial in fields like finance for interest calculations, biology for population studies, and physics for phenomena like radioactive decay.


