Master Logarithms: Free Expanding and Condensing Worksheet

Understanding Logarithms

Logarithms are essential tools in mathematics, particularly for solving exponential equations. They're incredibly useful in a wide range of applications including computer science, biology, and finance. In this post, we'll delve into how to manipulate logarithmic expressions through expansion and condensation, providing you with a comprehensive worksheet to master these skills.
What are Logarithms?

A logarithm (log) is the inverse operation to exponentiation. If y = b^x, then the logarithm of y to the base b is x, or logb(y) = x. Here are some fundamental rules and properties:
- Product Rule: log_b(MN) = log_b(M) + log_b(N)
- Quotient Rule: log_b(M/N) = log_b(M) - log_b(N)
- Power Rule: log_b(M^p) = p * log_b(M)
- Change of Base Formula: log_b(a) = log_c(a) / log_c(b)
Expanding Logarithms
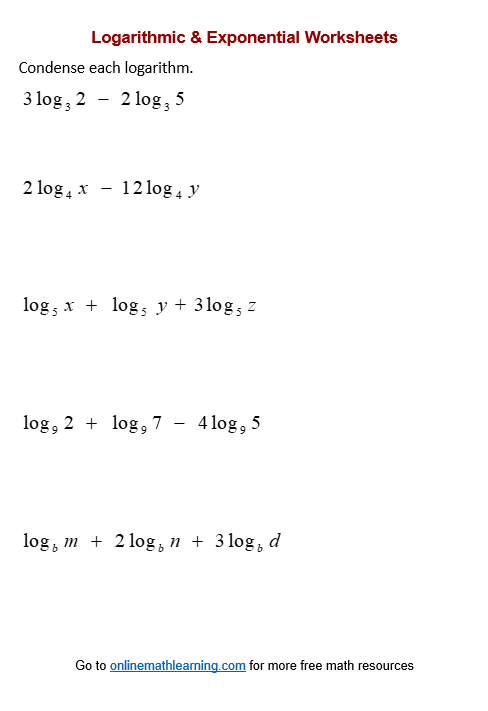
Expanding logarithms means transforming a single logarithmic expression into multiple logs using the product, quotient, and power rules. Here’s how to expand various logarithmic expressions:
Using the Product Rule

To expand a logarithm of a product, you simply sum the logarithms of the factors:
- log_b(MN) = log_b(M) + log_b(N)
For instance, if you have log2(8 * 16):
- Expand it: log2(8) + log2(16)
Using the properties of logarithms, this becomes:
- 3 + 4 = 7
Using the Quotient Rule
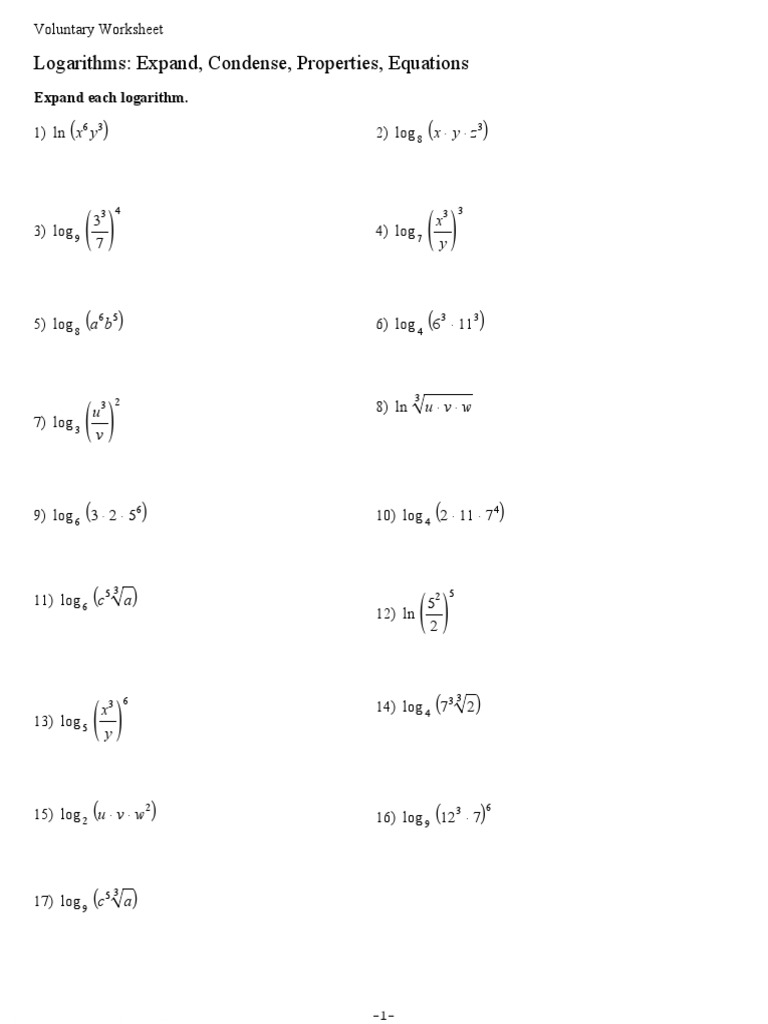
Similarly, for a quotient inside a logarithm, you subtract the logarithm of the denominator from the numerator:
- log_b(M/N) = log_b(M) - log_b(N)
An example would be log3(12⁄4):
- Expand it: log3(12) - log3(4)
- Simplify: log3(3 * 4) - log3(4) = log3(3) + log3(4) - log3(4) = log3(3) = 1
Using the Power Rule

When you have a power inside a logarithm, you multiply the exponent by the logarithm of the base:
- log_b(M^p) = p * log_b(M)
Consider log4(16^2):
- Expand: 2 * log4(16)
- Since 16 = 4^2, it becomes 2 * (2 * log4(4)) = 2 * (2 * 1) = 4
⚠️ Note: When expanding, make sure to follow the order of operations (PEMDAS).
Condensing Logarithms

Condensing logarithms involves combining separate logarithmic expressions into a single log. Here are the steps:
Using the Product and Quotient Rules

To condense logarithms:
- Sum or subtract logs by transforming them into one logarithm using the product rule or quotient rule.
Let's condense log2(x) + log2(y):
- Combine: log2(x * y)
Or log3(8) - log3(4):
- Combine: log3(8/4) which simplifies to log3(2)
Using the Power Rule

If the log involves an exponent, you can move it to the front:
- 3 * log5(4) can be condensed to log5(4^3) = log5(64)
📝 Note: Be careful with the change of base formula; sometimes you might need it to condense multiple base logs into a single base log.
Worksheet: Expanding and Condensing Logarithms

Here's a worksheet to practice what you've learned. Try these problems to test your understanding:
| Problem | Expand/Condense |
|---|---|
| 1. log2(2x) | Expand |
| 2. log3(81) + log3(9) | Condense |
| 3. log5(125/5) | Expand |
| 4. 2 * log10(100) - log10(10) | Condense |
| 5. log2(x^3) + log2(x^2) | Condense |

This summary helps in appreciating how we can manipulate logarithmic expressions for simplification and problem-solving. Whether expanding or condensing, the laws of logarithms provide a structured approach to handling complex logarithmic equations. This understanding is foundational for further mathematical exploration, such as logarithms in calculus, or for practical applications in fields requiring logarithmic scales like seismology or chemistry.
Why is it important to know how to expand and condense logarithms?

+
Understanding how to expand and condense logarithms is crucial for simplifying complex expressions, solving exponential and logarithmic equations, and analyzing logarithmic functions in various scientific and engineering contexts.
Can the change of base formula be used in both expanding and condensing?

+
Yes, the change of base formula is useful for both expanding logs when the base doesn’t match the problem’s requirements and for condensing when you need to combine logarithms of different bases into a single base.
How can I check if my expansion or condensation is correct?

+
You can verify your work by either reverse condensing an expansion or expanding a condensed form back to the original expression. Also, using a calculator to compute the original and manipulated logs can provide a numerical check.