5 Proven Techniques for Divisibility Worksheets
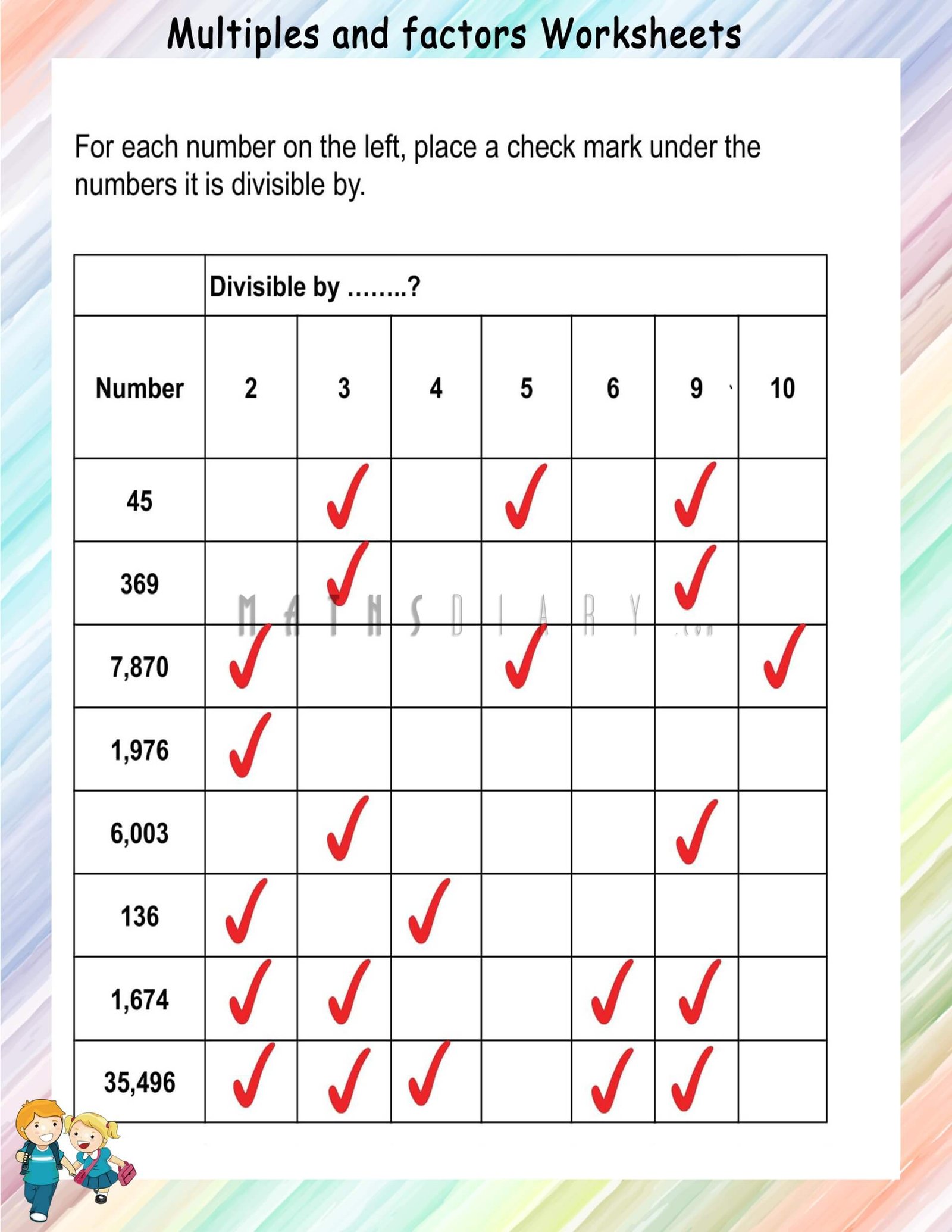
Divisibility is a fundamental concept in mathematics, serving as the cornerstone for a vast range of numerical operations and theories. For students and learners, mastering divisibility isn't just about rote learning but about understanding the underlying patterns and rules. In this comprehensive guide, we will explore 5 Proven Techniques for Divisibility Worksheets that educators and learners can employ to make the learning process both engaging and effective.
Understanding Divisibility


Before diving into the techniques, let’s clarify what divisibility means. A number is said to be divisible by another if it can be divided by that number without leaving a remainder. For example, 20 is divisible by 4 because 20 divided by 4 equals 5 with no remainder.
Technique 1: Visual Learning through Patterns

Visualization helps in grasping abstract concepts like divisibility:
- Create Division Grids: Draw grids where each row represents a multiple of a particular number. This visualizes how numbers align with divisibility rules.
- Color Coding: Use colors to highlight multiples of different numbers, helping students recognize patterns.

📝 Note: Visual techniques cater to various learning styles and can significantly aid in understanding complex math concepts.
Technique 2: Storytelling and Real-Life Examples

Integrating real-life scenarios into lessons:
- Share stories where numbers play a crucial role, like baking cookies or dividing goods in ancient times.
- Create Word Problems: Use scenarios where numbers naturally fit into divisibility rules, making the math relevant.
By doing so, students can relate to the mathematical concept and see how it applies to everyday situations.
Technique 3: Interactive Divisibility Games

Games make learning fun and interactive:
- Number Line Hop: Mark numbers on the floor or a board. Students hop to multiples of a specific number, reinforcing the concept of divisibility.
- Divisibility Puzzles: Develop puzzles where students must find numbers divisible by others to solve clues.
| Game Type | Description |
|---|---|
| Divisibility Bingo | Fill bingo cards with numbers, call out a number, and players mark off numbers that are divisible by it. |
| Card Games | Create rules where players must discard cards that are multiples of a chosen number, enhancing quick recognition. |

Technique 4: Digital Tools and Apps

Leveraging technology for an immersive learning experience:
- Interactive Apps: Use apps that allow students to input numbers and see immediate feedback on divisibility.
- Online Simulations: Virtual manipulatives where students can drag numbers into groups to understand divisibility visually.
💡 Note: Technology in education can break down barriers in understanding complex math topics like divisibility.
Technique 5: Collaborative Learning and Peer Teaching

Encouraging students to learn from and teach each other:
- Group Activities: Arrange students in groups where they solve divisibility worksheets together, fostering discussion and problem-solving skills.
- Peer Teaching: Assign more advanced students to teach divisibility rules to their peers, reinforcing their own understanding.
This approach not only strengthens the understanding of divisibility but also builds teamwork and communication skills.
To wrap things up, mastering the techniques for divisibility worksheets offers an engaging and effective pathway for both teaching and learning this essential math concept. From visual aids to digital tools, games to collaborative learning, these methods cater to different learning styles and provide a multi-faceted approach to understanding divisibility. By embedding these strategies into your teaching or study sessions, you create a vibrant learning environment where students can connect with math in a meaningful way, seeing numbers not as abstract concepts but as a part of the world they live in.
What is divisibility?

+
Divisibility refers to the ability of a number to be divided by another number without leaving a remainder. For example, 15 is divisible by 3 because 15 divided by 3 equals 5 with no remainder.
Why is understanding divisibility important in mathematics?

+
Divisibility plays a crucial role in various mathematical fields like algebra, number theory, and arithmetic. It helps in simplifying problems, solving equations, understanding number sequences, and even cryptography.
Can divisibility rules be applied to any number system?

+
Most divisibility rules are tailored for the decimal number system, but similar rules can be adapted for other number systems like binary or hexadecimal based on their specific mathematical properties.
How can students practice divisibility?

+
Students can practice with worksheets, engage in games that involve recognizing multiples, use online tools for instant feedback, and participate in group activities where they teach and learn from peers.