5 Essential Intermediate Value Theorem Practice Tips
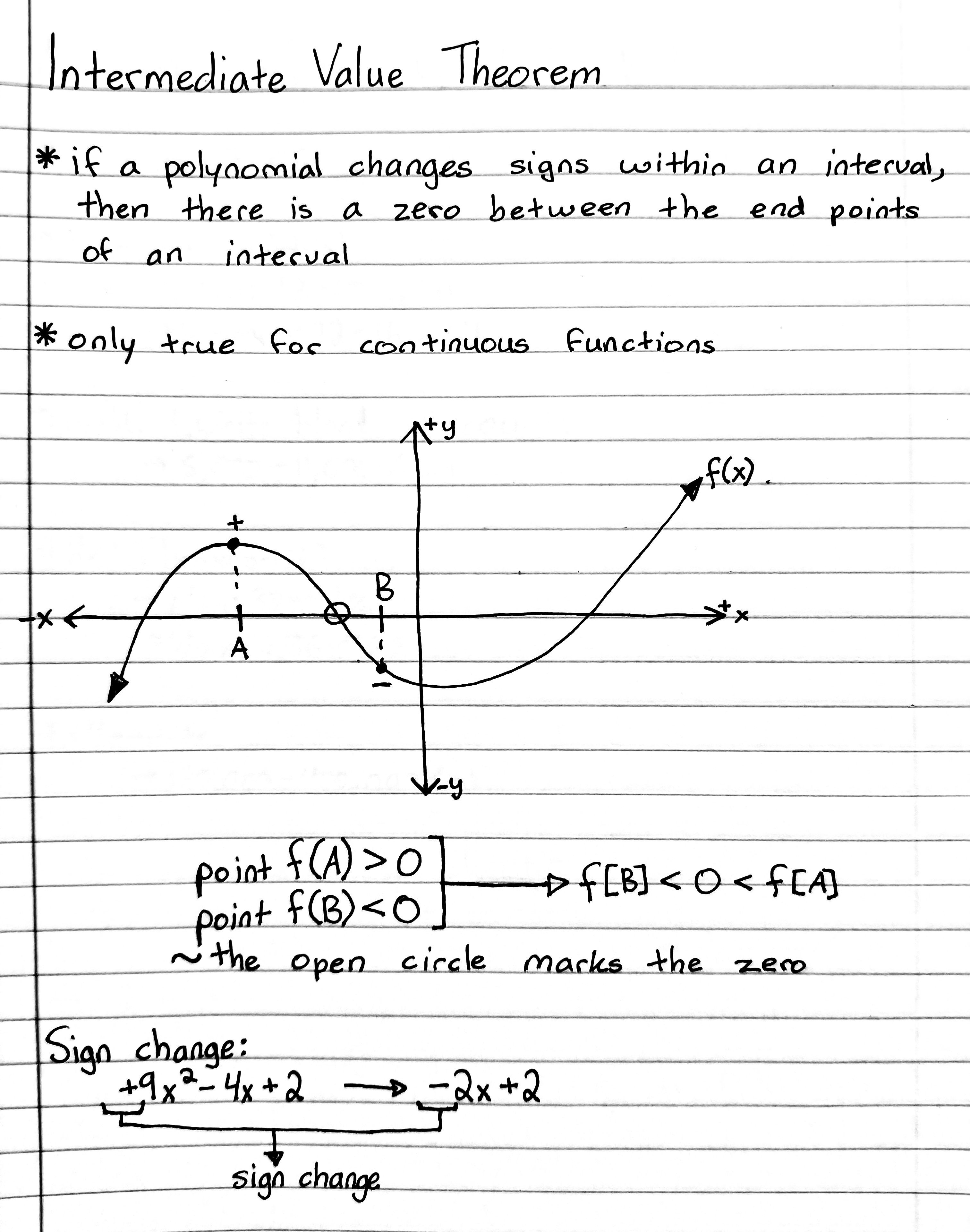
The Intermediate Value Theorem is a cornerstone of real analysis, providing insight into how continuous functions behave on intervals. It states that if a function f is continuous on a closed interval [a, b] and k is any number between f(a) and f(b), there exists some c in (a, b) such that f(c) = k. This theorem has practical applications in solving equations and understanding the continuity of functions. Here are five essential tips for practicing and mastering this fundamental theorem:
Understand the Theorem’s Preconditions

Before diving into problems, ensure you understand the preconditions of the Intermediate Value Theorem:
- The function must be continuous on the interval [a, b].
- The theorem is only applicable to closed intervals or when considering the extended real number line.
- The value k must lie between f(a) and f(b).
⚠️ Note: If any of these conditions are not met, the theorem doesn’t guarantee the existence of c.

Practice With Polynomial Functions

Polynomial functions are excellent for Intermediate Value Theorem practice because:
- Polynomials are continuous everywhere, making them perfect candidates for IVT.
- They can easily model real-life problems like growth rates or physical phenomena.
- The Rolle’s Theorem is a particular case of IVT, making polynomials a good starting point.
Here’s an example:
f(x) = x^3 - x + 2 f(0) = 2, f(1) = 2 Is there any c in (0, 1) such that f© = 1?
📝 Note: While solving, remember to sketch the function for better visualization.

Work on Real-Life Scenarios

Applying the theorem to real-life situations not only tests your understanding but also shows its practical utility:
- Economics: Finding equilibrium points where supply equals demand.
- Physics: Determining critical points in motion, like a ball thrown vertically with zero velocity at some point.
- Biology: Analyzing population growth models to predict when a population reaches a particular threshold.
| Application | Function | IVT Use |
|---|---|---|
| Economics | Supply-Demand Curves | Find equilibrium price |
| Physics | Velocity-Time Equation | Identify when velocity is zero |
| Biology | Logistic Growth Model | Determine carrying capacity or inflection points |

Link IVT With Other Theorems

Connecting the Intermediate Value Theorem with other mathematical concepts can deepen your understanding:
- Rolle’s Theorem: A specific case of IVT where the function equals zero.
- Bolzano’s Theorem: An algebraic version of IVT where a continuous function crosses the x-axis.
- Extreme Value Theorem: Relates to finding maximum and minimum values which can be used with IVT.
💡 Note: Linking theorems helps in solving complex problems that involve multiple calculus concepts.

Explore Counter-Examples

Understanding where the Intermediate Value Theorem fails can solidify your grasp:
- Discontinuous functions:
- A function with a jump discontinuity or an asymptotic behavior might not satisfy IVT.
- Open intervals:
- IVT does not apply to open intervals as they exclude endpoints.
- Finding counterexample functions can illustrate limitations:
- For instance, f(x) = 1/x for x in (-∞, 0) ∪ (0, ∞) doesn’t satisfy IVT.
In practice, the Intermediate Value Theorem provides a robust tool for not just solving equations but also for understanding the behavior of functions. By focusing on preconditions, practicing with polynomials, exploring real-life applications, linking with other theorems, and understanding counterexamples, you can enhance your mastery of this theorem. This understanding not only makes problem-solving easier but also deepens your appreciation of mathematical continuity and its implications in various fields.
What is the Intermediate Value Theorem used for?

+
The Intermediate Value Theorem (IVT) is primarily used to prove the existence of roots or points where a continuous function takes on a particular value within an interval. It is crucial in fields like economics for finding equilibrium points, in physics for analyzing motion, and in various mathematical proofs to assert the existence of solutions.
Can the Intermediate Value Theorem find exact values?

+
No, the theorem only guarantees the existence of at least one value within the interval where the function takes on the desired value. Finding the exact value typically requires numerical methods like the bisection method or graphical approaches.
What are the limitations of the Intermediate Value Theorem?

+
IVT does not work if the function is not continuous on the interval, or if the interval is not closed. It also does not provide the number of solutions, nor does it help with discontinuous functions or infinite intervals.
How can I practice Intermediate Value Theorem problems?

+
Start with simpler polynomial functions to understand continuity and applications. Then, move to real-life scenarios where continuity is key. Also, engage with related theorems to understand the full scope of IVT.