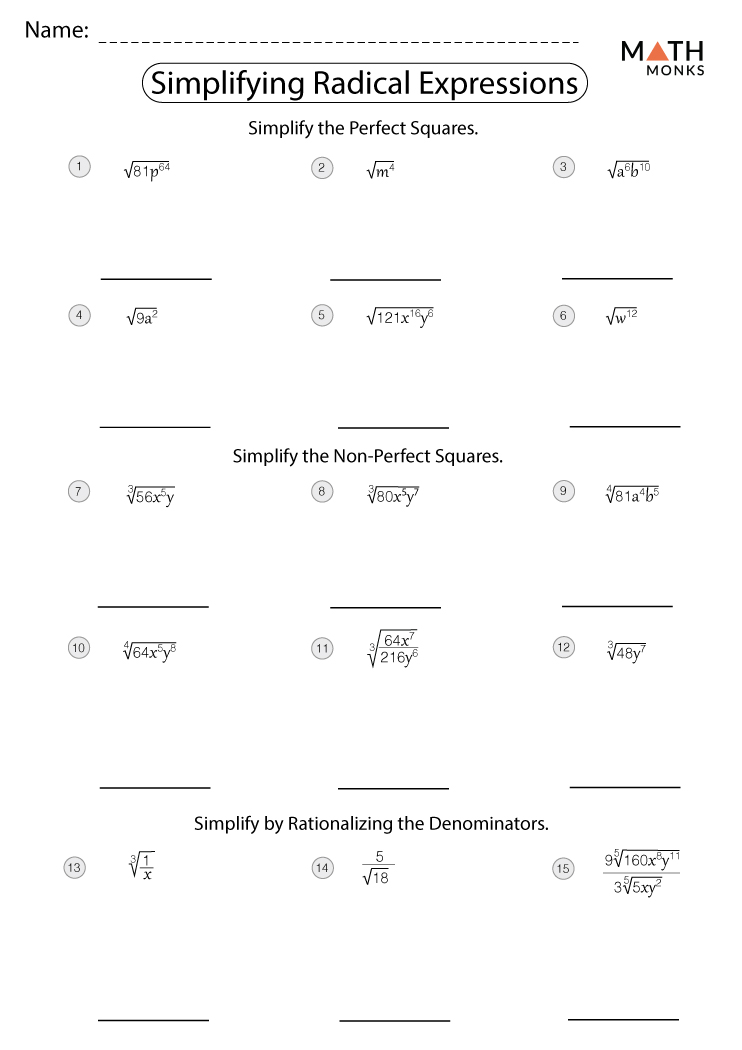
Dividing Monomials Worksheet Answers: Simplified Solutions for Students
Monomials are algebraic expressions consisting of one term only, such as 3x, 5y2, or -8x3y. In mathematics, students often encounter the need to divide one monomial by another, simplifying the resulting expression. This process can seem challenging at first, but with practice and understanding, it becomes quite manageable. Here, we'll provide you with a detailed guide on how to divide monomials, complete with a worksheet for practice and answers for you to check your work.
Understanding Monomials and Division

Dividing monomials involves the division of coefficients and the subtraction of exponents. Here are the basic steps:
- Divide the coefficients: This part is straightforward. Simply divide the numerical coefficients of the monomials.
- Subtract the exponents: If the variable is the same, subtract the exponent of the divisor from the exponent of the dividend.
- Combine the variable: After simplifying, write down the variable with the new exponent.
Let's look at a simple example:
- (15x3) / (5x)
- Coefficient division: 15 ÷ 5 = 3
- Exponent subtraction: 3 - 1 = 2
- Result: 3x2
Practice Worksheet: Dividing Monomials
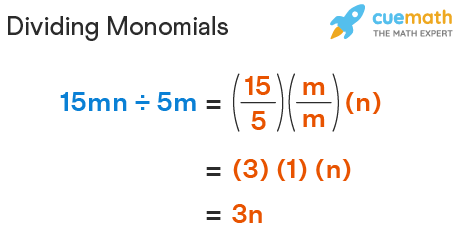
To help you practice, here's a simple worksheet for dividing monomials. Below each problem, you'll find the step-by-step solution for your reference.
| Problem | Solution |
|---|---|
| (12a4) / (3a) |
|
| (27b5) / (9b2) |
|
| (-8c4d3) / (2c2d) |
|
| (16x7y3) / (4x5y2) |
|

📌 Note: When dealing with variables, always ensure that the base is the same before subtracting exponents. If the bases are different, you can't simplify them further in terms of their variables.
Handling Powers of Variables

When the monomials include powers of the same variable, we subtract the exponents:
- (x10) / (x4) = x10-4 = x6
- If a variable's exponent becomes zero after subtraction, it essentially means that the term is equal to 1:
- (x5) / (x5) = x5-5 = x0 = 1
Multiplying and Dividing Monomials

Dividing monomials can also be understood through multiplication by the reciprocal:
- Example: (6x3) / (2x2) = (6x3) * (1/2) * (1/x2) = 3x3-2 = 3x
This method can be particularly useful when dealing with complex monomials or when you're more comfortable with multiplication.
To conclude, understanding how to divide monomials is essential for any student tackling algebra. By breaking down each part of the monomial and applying the division rule, you simplify expressions effortlessly. The provided worksheet will give you practical experience, while the explanations ensure you understand the underlying principles. Keep practicing, and you'll master this critical skill in no time, paving the way for tackling more complex algebraic expressions.
Why is it important to know how to divide monomials?

+
Understanding how to divide monomials is crucial for simplifying and solving algebraic expressions, which forms the basis of many mathematical concepts and applications in physics, engineering, economics, and more.
What happens if the exponents are negative?

+
When dividing monomials with negative exponents, you follow the same rule of subtracting exponents. If the result is negative, it indicates that the term moves from the numerator to the denominator or vice versa, keeping the positive exponent in the new location.
Can you divide monomials with different bases?

+
Generally, monomials with different bases cannot be divided directly because the division of variables only applies when they have the same base. However, if there’s a constant factor common to both bases, you can factor this out before dividing.