Simplify Radicals: Operations Worksheet Guide

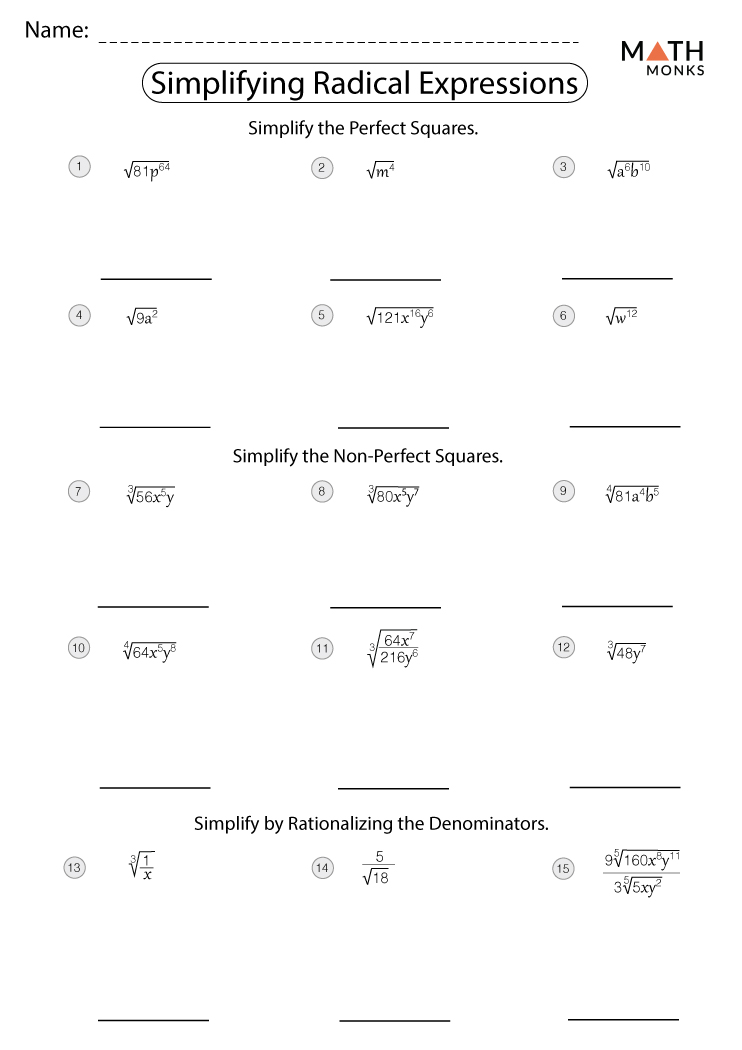
Understanding and simplifying radicals is a fundamental skill in algebra, often necessary for solving equations and simplifying expressions. Whether you're a student grappling with square roots, cube roots, or other nth roots, or an educator looking to guide students through the process, mastering how to simplify radicals can significantly enhance problem-solving abilities. This comprehensive guide will take you through simplifying radicals, including different methods, tips, and common misconceptions to avoid.

The Basics of Radicals

Radicals are mathematical expressions that denote the nth root of a number. The most common radicals are:

• Square roots (√x): the number that, when multiplied by itself, gives the number inside the radical.
• Cube roots (³√x): the number that, when raised to the third power, equals the number under the radical.
• Nth roots (ⁿ√x): the number which raised to the power of n equals x.

What is Simplifying Radicals?

Simplifying radicals involves converting an expression into its most reduced or simplest form by factoring out perfect roots. Here's the basic concept:

• If a² = b, then a is the square root of b.
• If a³ = b, then a is the cube root of b.

To simplify, we look for factors of the number under the radical that are perfect squares or perfect cubes or the corresponding n-th powers, and then pull them outside the radical.

Step-by-Step Guide to Simplify Radicals

To simplify radicals, follow these steps:

1. Factorize the Number Under the Radical

Break down the number inside the radical into its prime factors. For example:

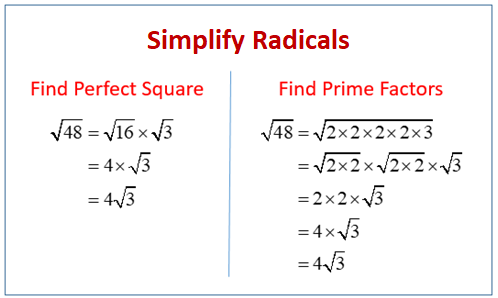
• √56 = √(2 × 2 × 2 × 7)

2. Group and Pull Out Perfect Roots

If you find a pair of factors that are the same, you can take one out of the square root. For cube roots or higher, you’ll need sets of three or n factors respectively:

• √(2 × 2 × 2 × 7) = 2√(2 × 7)

3. Multiply Factors Outside the Radical

Multiply the numbers you’ve taken outside the radical sign:

• 2√14 = 2√14

4. Continue Simplifying

Simplify the remaining radicand if possible. Sometimes, you might need to use a calculator for very large numbers:

• √28 = √(2 × 2 × 7) = 2√7 (This is the simplest form)

Important Notes

🔍 Note: The process described above applies to rationalizing the denominator as well, where we remove radicals from the denominator to make the expression look cleaner.

Advanced Techniques for Simplification

5. Rationalizing the Denominator

If you have a fraction with a radical in the denominator, multiply both the numerator and the denominator by the conjugate or a suitable form of the denominator:

• 1/√2 can be rationalized by multiplying by √2/√2 to get √2/2.

6. Simplifying Higher Order Radicals

When dealing with fourth roots, fifth roots, and beyond, the process involves recognizing perfect squares within the radicand for even roots or the corresponding sets for odd roots:

• ⁴√16 = 4√1, since 2⁴ = 16
• ⁵√-32 = -2, since (-2)⁵ = -32

Practice and Understanding

To truly grasp simplifying radicals, practice is essential. Here are some exercises:

• Simplify √32
• Rationalize the denominator of 5/√7
• Find the cube root of -125

Common Misconceptions and Tips

Here are some common mistakes to avoid:

• Adding Radicals: Only radicals with the same radicand can be added or subtracted directly. For example, √2 + √3 cannot be simplified further; they are not like terms.
• Multiplying/Dividing Radicals: Remember that the product and quotient rules apply: √a * √b = √(ab), and similarly for division.
• Negative Radicands: When simplifying roots of negative numbers, use imaginary units for odd roots (e.g., ³√-8 = -2i).

💡 Note: Always verify your work; a calculator can be helpful for checking your simplified radicals.

In Summation

We’ve delved into the essentials of simplifying radicals, covering the foundational concepts to more advanced techniques. From factoring prime numbers to handling higher-order roots and rationalizing denominators, each step enhances your proficiency in algebra. The journey through algebra is one of discovery, where each simplified radical not only represents a step towards solving equations but also illustrates the elegance of mathematical principles. Keep practicing, reviewing these methods, and you’ll find that simplifying radicals becomes a natural and effortless skill.

Why do we simplify radicals?

+

Simplifying radicals helps in reducing complex expressions to simpler forms, making them easier to work with in further calculations or to understand their true value.

Can you simplify radicals with variables?

+

Yes, you can simplify radicals with variables by treating them like numbers. For example, √16x² = 4|x| if x is not negative, simplifying as with constants but considering the absolute value for even roots.

What is the difference between a square root and a cube root?

+

A square root (√x) finds a number that, when squared, gives x, while a cube root (³√x) finds a number whose cube is x.