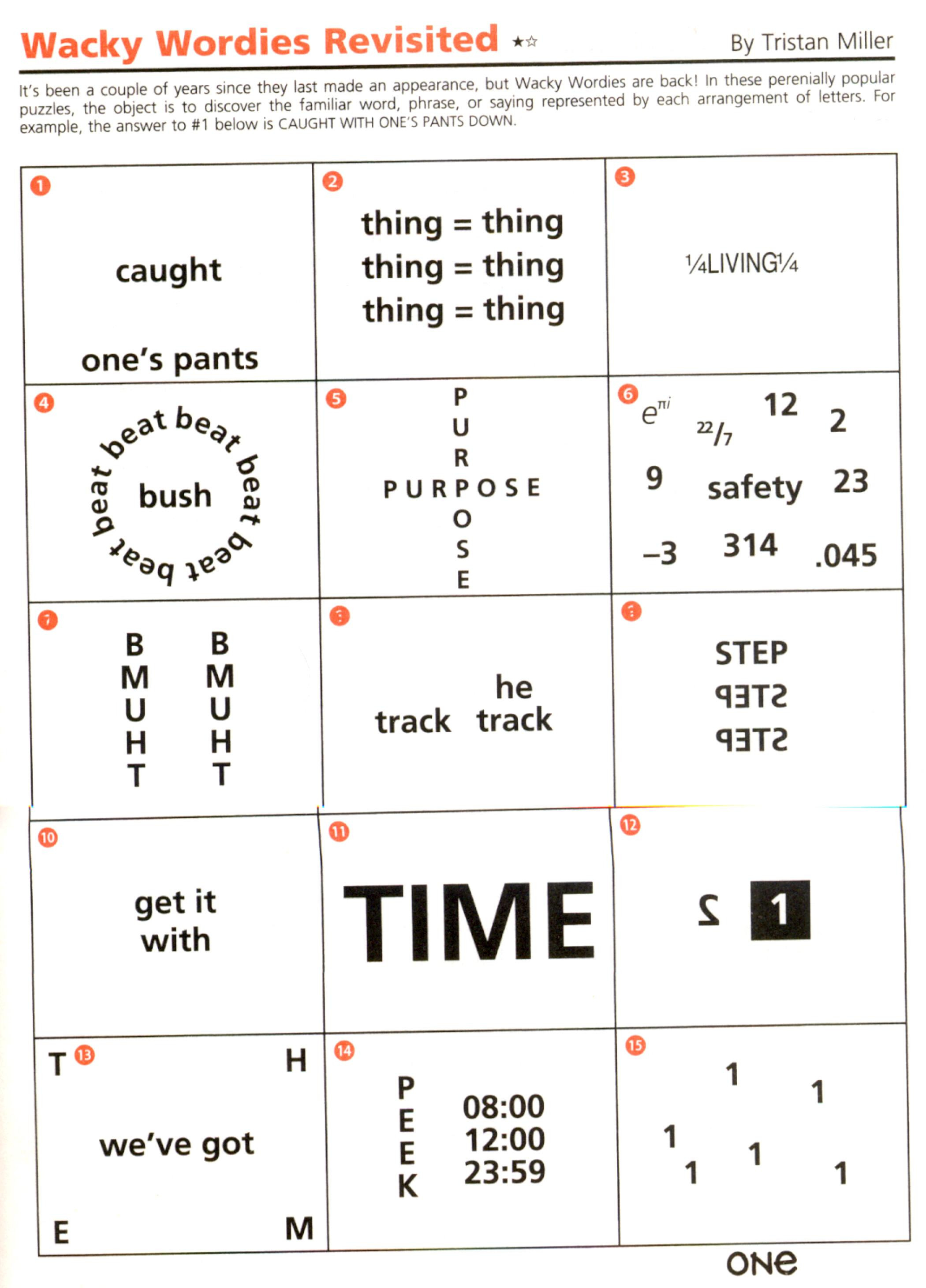
Master Cos Sin Tan with Our Simple Worksheet

Mathematics often appears daunting, especially when it comes to trigonometry. However, mastering cosine (cos), sine (sin), and tangent (tan) can be both fun and straightforward. With our simple worksheet, you'll not only understand these trigonometric functions better but also apply them with confidence in various contexts.
What Are Cos, Sin, and Tan?

Let’s begin with a brief introduction to these trigonometric functions:
- Cosine (cos): This function relates an acute angle in a right triangle to the ratio of the adjacent side to the hypotenuse.
- Sine (sin): It’s the ratio of the side opposite the angle to the hypotenuse.
- Tangent (tan): It is the ratio of the opposite side to the adjacent side.
Using the Trigonometric Worksheet

Our worksheet is designed to guide you step-by-step through the world of trigonometry:
1. Understanding Right Triangles

Before diving into the functions, it’s crucial to understand the anatomy of a right triangle:
| Side | Description |
|---|---|
| Hypotenuse | The longest side, opposite to the right angle. |
| Opposite | The side directly opposite to the angle of interest. |
| Adjacent | The side next to the angle of interest but not the hypotenuse. |

📚 Note: Understanding these sides is fundamental to grasping trigonometric functions.
2. Calculating Cos, Sin, and Tan

Here’s how to calculate each function using a calculator or the formulas:
- Cos(θ) = adjacent/hypotenuse
- Sin(θ) = opposite/hypotenuse
- Tan(θ) = opposite/adjacent
With the worksheet, you'll be provided with various angles. You'll need to determine which sides correspond to each function and then calculate the values.
3. Practical Applications

The real beauty of trigonometry lies in its application. The worksheet includes scenarios like:
- Calculating the height of a building given the angle of elevation and a known distance.
- Determining the distance across a lake if you’re on one side and know the angles of two markers on the opposite side.
4. Practice Makes Perfect

Our worksheet includes a series of problems, progressively challenging:
- Basic calculations for angles of 30°, 45°, and 60°.
- Real-world problems where trigonometric functions need to be applied.
- A final quiz to test your mastery.
Tips for Success

Here are some tips to excel in your trigonometric journey:
- Memorize the basic angles (0°, 30°, 45°, 60°, 90°) and their exact values for cos, sin, and tan.
- Use a reference sheet or calculator for more complex angles if necessary, but strive to remember basic values.
- Always label your triangles to avoid confusion.
- Practice regularly, especially applying these functions to solve problems.
Remember, trigonometry is not just about numbers; it's about understanding the relationship between angles and lengths. As you work through the problems, you'll gain insight into this fascinating subject.
As we wrap up, consider how trigonometry extends far beyond school mathematics. It's used in:
- Astronomy to measure distances to stars.
- Engineering for structural analysis.
- Navigation, both at sea and in the air, to find bearings and distances.
These diverse applications underscore the importance and beauty of mastering cos, sin, and tan. With our simple worksheet, you're well-equipped to not only solve these problems with ease but also appreciate the underlying principles. Keep practicing, and soon you'll find trigonometry to be an invaluable tool in your mathematical toolkit.
What’s the easiest way to remember trigonometric identities?

+
A helpful mnemonic is SOHCAHTOA: Sine is Opposite over Hypotenuse, Cosine is Adjacent over Hypotenuse, and Tangent is Opposite over Adjacent.
How can I use trigonometry in everyday life?

+
Trigonometry is used in activities like:
- Determining heights and distances, like how tall a tree is without climbing it.
- Analyzing waves in physics for sound or water.
- Understanding cycles in data for various analyses.
Can you use trigonometry in graphic design?

+
Yes, trigonometric functions help in creating precise angles and dimensions for design elements, and can be used in:
- Placing objects on a grid for proper perspective.
- Calculating proportions and sizing of elements.
- Creating circular or angular motion graphics.