Mastering Quadratic Functions: Attributes Worksheet Explained
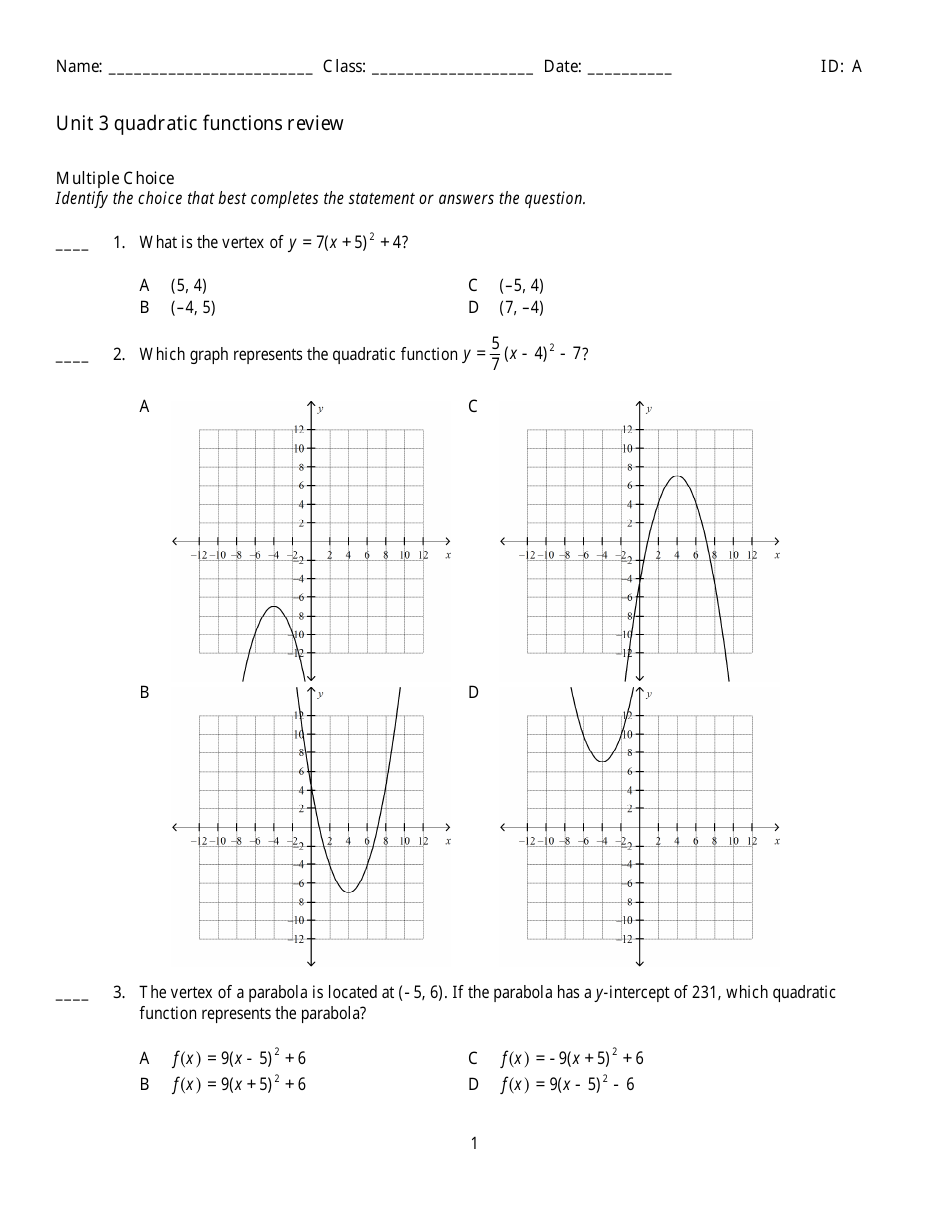
Quadratic functions are a fundamental part of algebra that anyone studying or working with mathematics should be comfortable with. This post dives deep into the intricacies of quadratic functions, focusing on an often-used tool for understanding them: the quadratic functions attributes worksheet. Here, we'll explore how to dissect, analyze, and appreciate the beauty and complexity of these functions through a structured worksheet format.
What is a Quadratic Function?

A quadratic function is generally represented in the form:
ax² + bx + c = 0, where a ≠ 0, b, and c are constants. The graph of such a function is a parabola. Here’s a brief overview of its attributes:
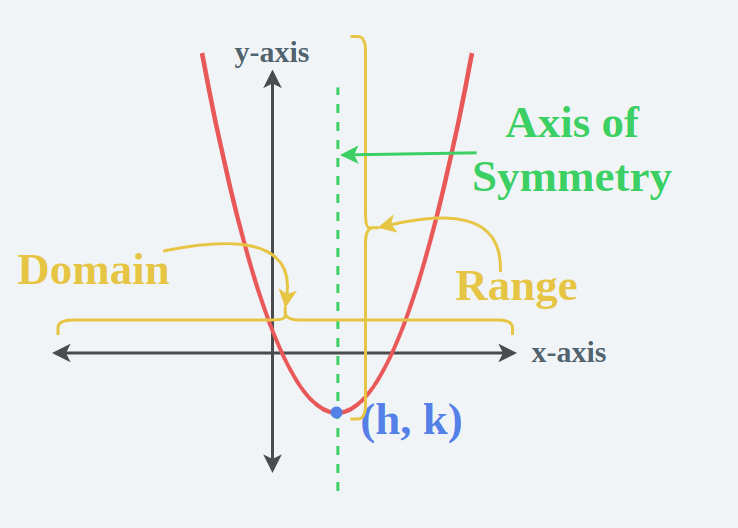
- Vertex - The turning point of the parabola.
- Axis of Symmetry - The vertical line that divides the parabola into two symmetric halves.
- Maximum or Minimum Value - Depending on whether the parabola opens up or down.
- Roots - Where the parabola intersects the x-axis, if at all.
The Attributes Worksheet Explained

The quadratic functions attributes worksheet is designed to:
- Clarify the parabola’s key features through mathematical operations and analysis.
- Provide structured practice to reinforce understanding.
- Prepare students for more complex functions and real-world applications.
Step-by-Step Analysis
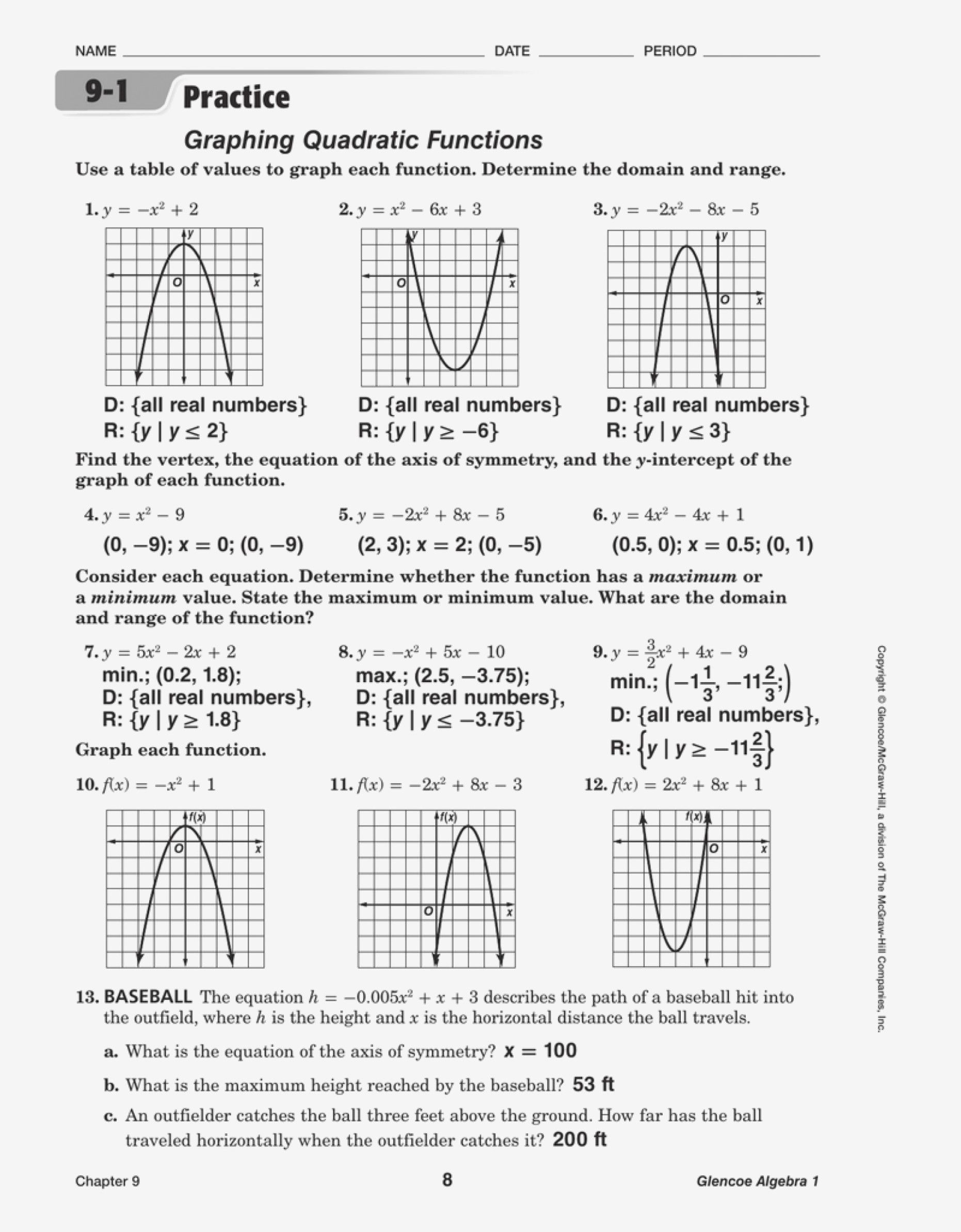
Here’s how you can systematically analyze a quadratic function:
- Identify the Standard Form - Determine the values of a, b, and c.
- Find the Vertex - Use the formula x = -b/(2a) to find the x-coordinate of the vertex, then substitute it into the function to find the y-coordinate.
- Determine the Axis of Symmetry - The axis of symmetry is simply the vertical line x = -b/(2a).
- Calculate the Roots - Solve the equation ax² + bx + c = 0 using the quadratic formula:
- x = (-b ± √(b² - 4ac)) / 2a
- Find the Y-Intercept - Simply evaluate the function at x = 0.
- Identify the Direction of Opening - If a > 0, the parabola opens up; if a < 0, it opens down.
- Analyze the Extrema - The vertex tells you if the parabola has a maximum or minimum value.
💡 Note: Ensure to verify all results by graphing or by substitution to avoid algebraic errors.
Using a Table for Analysis

| Attribute | Formula/Method | Description |
|---|---|---|
| Vertex | x = -b/(2a) y = f(x) at vertex |
The highest or lowest point of the parabola. |
| Axis of Symmetry | x = -b/(2a) | Line that splits the parabola into mirror images. |
| Roots | Quadratic Formula | Where the parabola touches or crosses the x-axis. |
| Y-Intercept | f(0) | Where the parabola intersects the y-axis. |
| Direction of Opening | a > 0: up; a < 0: down | Determines if the parabola is a ‘U’ or an inverted ‘U’. |
Further Exploration
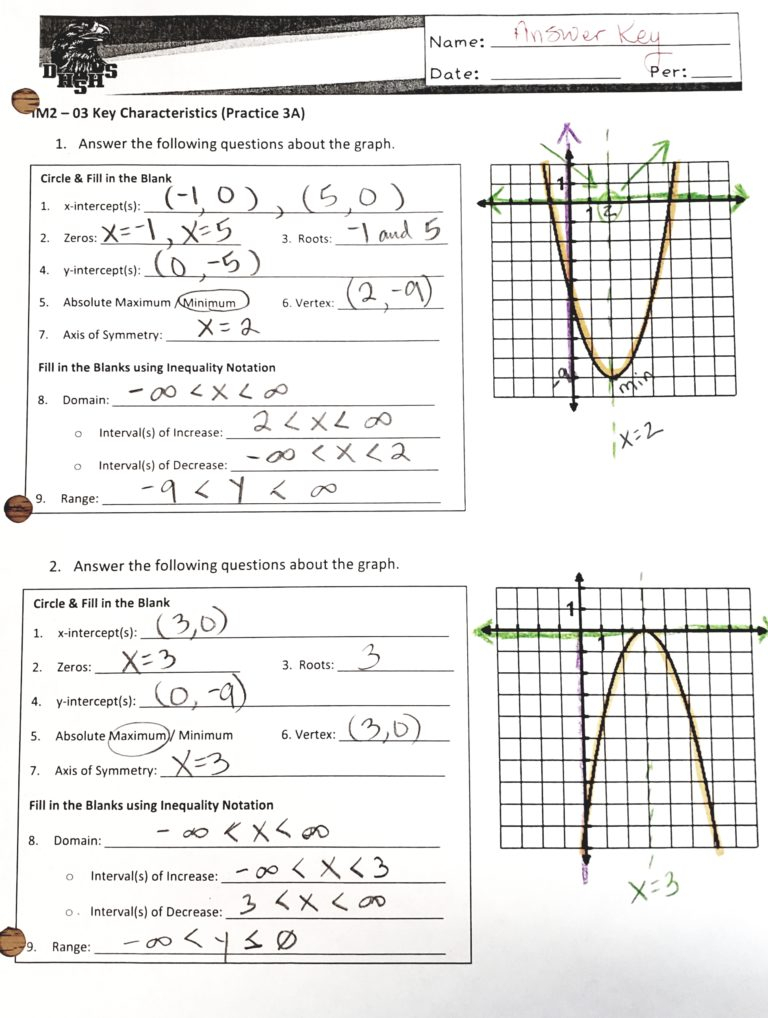
Once familiar with the basics, you might want to explore:
- Transformations of parabolas - shifting, reflecting, or stretching.
- Quadratic inequalities and their solutions.
- Applications of quadratic functions in physics, economics, and other fields.
- Complex roots and their implications in real-world scenarios.
To summarize, the quadratic functions attributes worksheet is a critical tool for understanding how quadratic functions work. By analyzing these key attributes, you not only grasp the mathematical concepts but also build the foundation for tackling more advanced mathematical structures. This systematic approach ensures that every aspect of a quadratic function is understood in depth, preparing you for real-world applications where quadratic functions are often seen, from predicting the path of a ball in sports to optimizing resource allocation in business.
What if I can’t find any roots?
+
If your calculations show no real roots, it means the parabola does not intersect the x-axis at any point. This is also known as having imaginary roots or complex roots, indicating that the discriminant (b² - 4ac) is less than zero.
Can the vertex be on the x-axis?

+
Yes, if the vertex is on the x-axis, the parabola touches the x-axis at that point. In this case, the vertex coincides with one of the roots of the function, and the quadratic has a double root.
How can I use quadratic functions in real life?

+
Quadratic functions are used to model various phenomena, like projectile motion, where height of an object can be described by a quadratic equation relative to time; in finance to optimize portfolios; in construction for the design of arches; and in biology to describe population growth rates.



