5 Ways to Master Area Calculations for Shapes
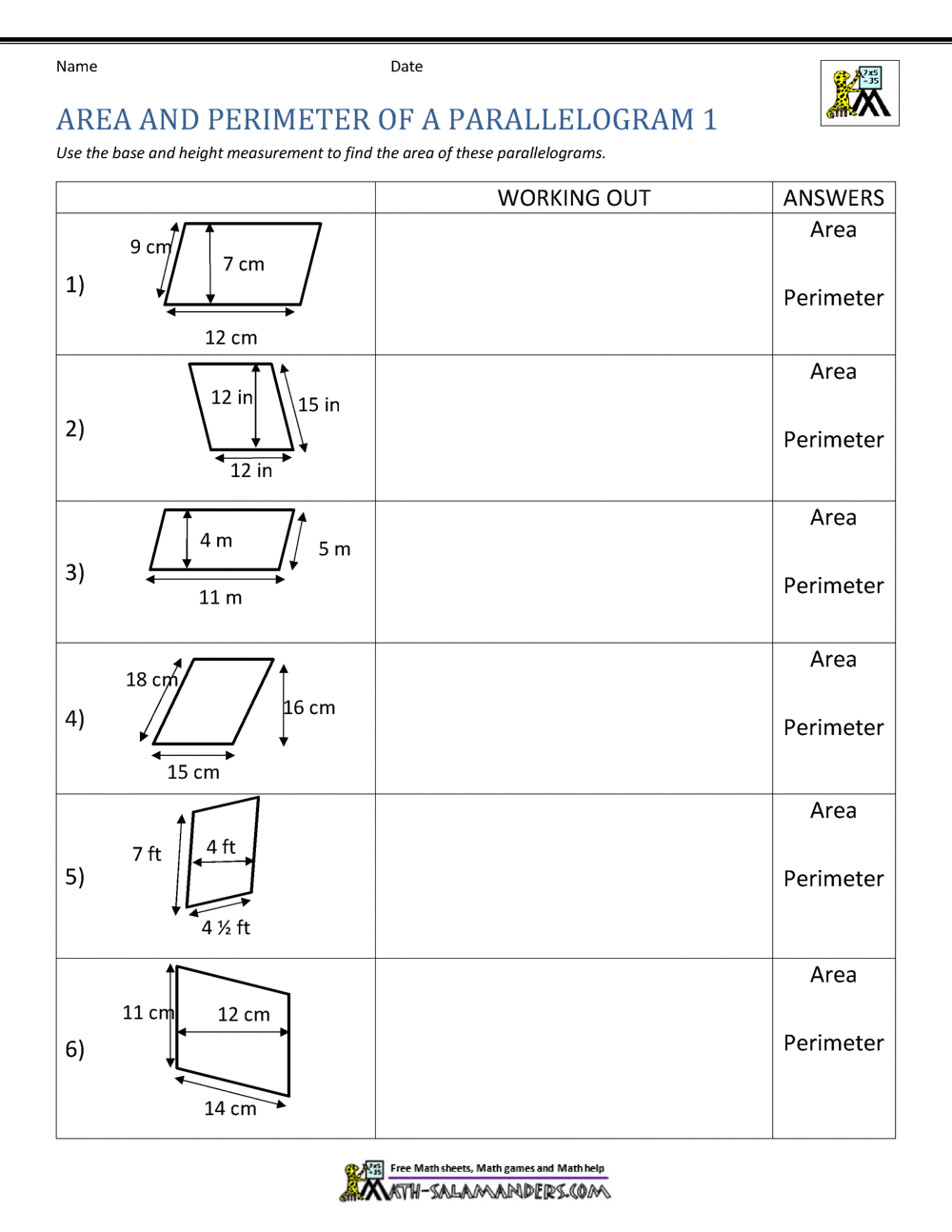
Calculations for different shapes are essential skills in various fields like architecture, engineering, mathematics, and even everyday tasks such as home improvement projects. Understanding how to accurately calculate the area of common geometric shapes can not only save time but also ensures precision in your work or projects. Here are five strategies to master area calculations for shapes:
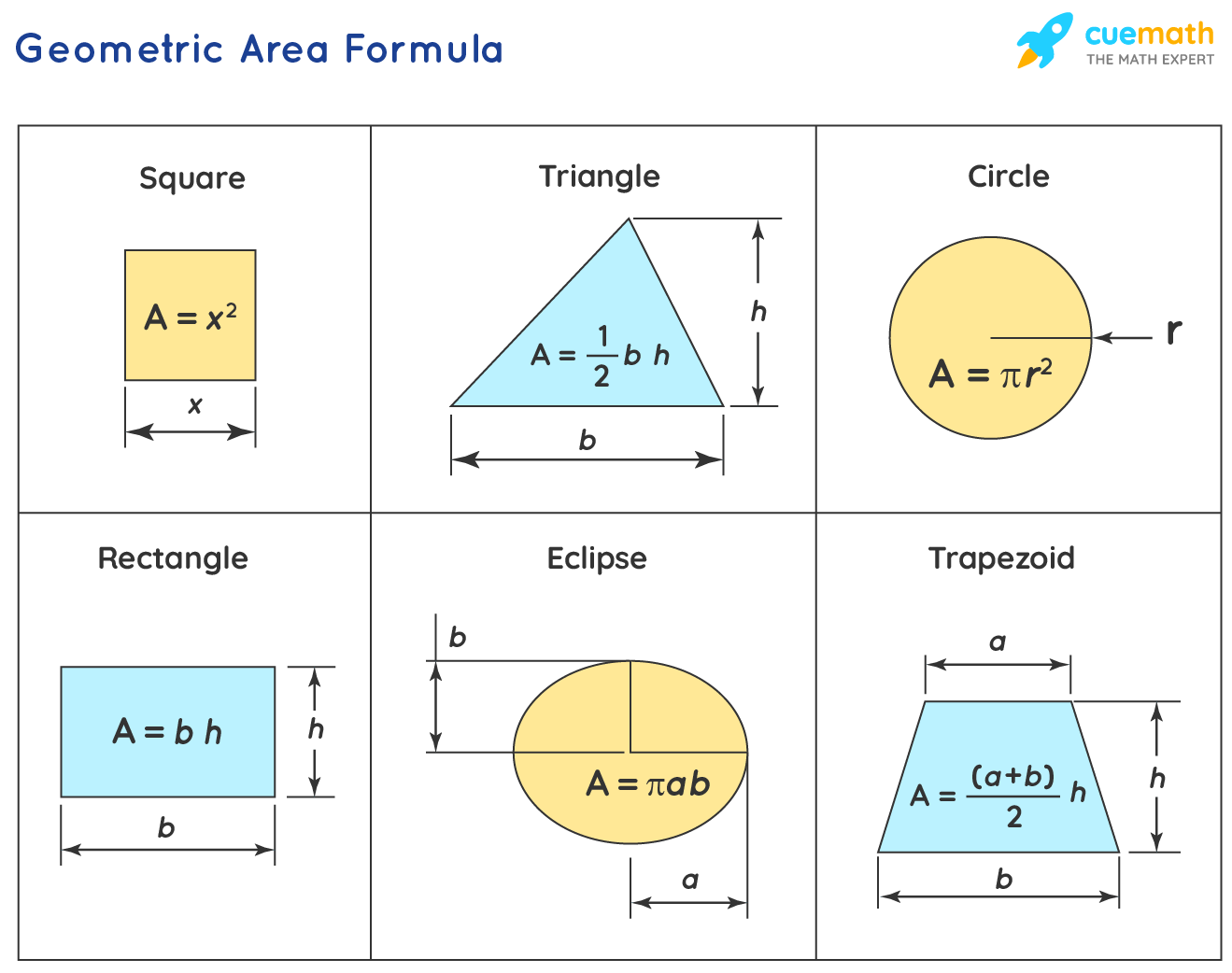
Understand the Formulas

Begin with understanding the basic formulas:
- Circle: Area = πr2
- Square: Area = s * s (side2)
- Rectangle: Area = l * w
- Triangle: Area = 0.5 * b * h
- Parallelogram: Area = b * h
- Trapezoid: Area = 0.5 * (a + b) * h
Commit these formulas to memory as they are the foundation of all calculations. Understanding the formulas means you can quickly identify the relevant measurements for each shape.
🎓 Note: For complex shapes or when a shape is made up of several basic shapes, breaking down the shape into recognizable parts can make the calculation easier.
Practice with Visual Tools

Utilize geometry software, apps, or even draw shapes on paper. Visual aids can:
- Help visualize how dimensions relate to formulas.
- Allow practice in measuring and applying formulas in real-time.
- Make the learning process engaging and less abstract.
Many online tools provide immediate feedback, so you can correct your calculations on the spot, fostering an environment where learning from mistakes is part of the process.
🛠️ Note: Applications like GeoGebra or Desmos provide excellent platforms for interactive geometry practice.
Learn to Estimate Before Calculating
Estimation:
- Provides a quick check to see if your calculated answer is in the ballpark.
- Helps in understanding the size of the shape even before any formal calculation.
- Is useful for rapid assessments in practical scenarios where exact measurements are not available.
Try to develop a sense of how big a given area is by comparing it to familiar shapes or objects. For instance, if you know the size of your room, you can roughly estimate the area of a similar shaped room in a new house without taking out a tape measure.
Implement Multi-Step Calculations

Complex shapes often require multiple steps to calculate:
- Break down the shape into simpler components.
- Calculate the area of each component using the basic formulas.
- Sum or subtract areas as needed to get the final area.
Here's an example:
| Shape | Calculation |
|---|---|
| Shape A | 15m2 + 12m2 |
| Shape B (subtracting a smaller shape) | 50m2 - 10m2 |

Use Dimensional Analysis

Dimensional analysis can ensure you're working with the correct units:
- Keep track of units of measurement to avoid calculation errors.
- Convert all units to a common measurement (e.g., square feet, meters2).
- Understand the relationship between different units to better visualize and estimate.
For example, when calculating the area of a room where one side is in feet and the other in inches, you'll need to convert both measurements to the same unit for an accurate calculation.
Mastering area calculations involves understanding formulas, visual practice, estimation, multi-step calculations, and using dimensional analysis. These strategies not only help in getting accurate results but also in understanding shapes in a deeper way. As you apply these methods, your proficiency in geometry will grow, allowing you to tackle increasingly complex shapes and calculations with confidence. Over time, the skills you've honed will become second nature, making area calculations seamless in both professional and everyday life.
Why is it important to estimate before calculating?
+
Estimation before calculating provides a sanity check for your work. If your calculated answer significantly deviates from your estimation, it’s a cue to recheck your calculations. Additionally, it’s a skill that’s valuable for quick assessments in various professional settings.
How do visual tools help in mastering area calculations?

+
Visual tools provide an interactive way to learn and understand how shapes relate to their formulas. They allow for immediate practice and correction, which aids in solidifying concepts.
Can dimensional analysis be applied to all geometric calculations?

+
Yes, dimensional analysis is a fundamental technique that ensures consistency in units, which is crucial for accurate calculations across different scales and measurements.
What to do if you encounter a shape with an unknown formula?

+
If you encounter a shape without a known formula, try to break it down into simpler, familiar shapes. Then calculate the area of these shapes and sum or subtract as required to get the total area of the unknown shape.



