Linear vs Nonlinear Worksheet: Simplify Your Math Learning

Mathematics, the cornerstone of logical reasoning and problem-solving, often presents students with two distinct pathways: linear and nonlinear equations. These paths can influence the complexity and approach to problem-solving. In this comprehensive exploration, we will delve into the intricacies of both linear and nonlinear equations, explore how they are represented, and discuss strategies to simplify your learning experience. Whether you're navigating through high school algebra or tackling advanced calculus, understanding the distinction between these two can significantly enhance your mathematical journey.
Understanding Linear Equations


Linear equations are the bread and butter of algebra. They can be expressed in the form:
y = mx + b
where:
- m is the slope of the line, determining its steepness.
- b is the y-intercept, where the line crosses the y-axis.
Linear equations are characterized by their:
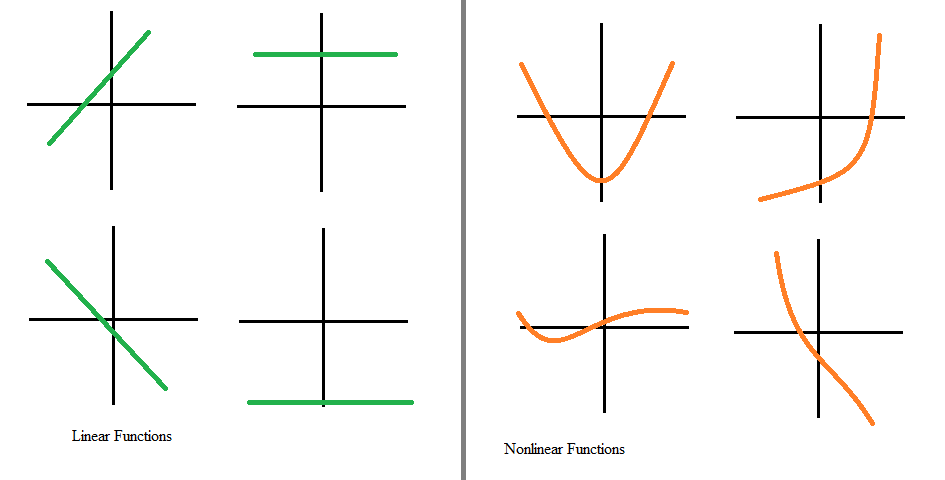
- Straight Line Representation: On a graph, they form a straight line.
- Constant Rate of Change: The slope ’m’ remains constant, meaning the value of y changes proportionally with x.
- Simple Solutions: They typically have one solution or infinite solutions in systems of equations.
Exploring Nonlinear Equations


Nonlinear equations, on the other hand, introduce a complexity that extends beyond the straight lines of linear math. These equations can take numerous forms such as:
- Quadratic: (y = ax^2 + bx + c)
- Polynomial: (y = ax^n + bx^{n-1} + … + k)
- Exponential: (y = ab^x)
- Logarithmic: (y = log_b(x))
These equations can be identified by:
- Nonlinear Curves: They might appear as parabolas, exponentials, or other curved graphs.
- Changing Rate of Change: The rate at which y changes with respect to x is not constant.
- Complex Solutions: They can have zero, one, two, or multiple solutions depending on the degree of the equation.
Comparing Linear and Nonlinear Equations

Here’s a comparison to understand their differences better:
| Feature | Linear Equations | Nonlinear Equations |
|---|---|---|
| Graphical Representation | Straight line | Curves or non-linear patterns |
| Rate of Change | Constant | Variable |
| Solutions | One or infinite | Various, from none to multiple |
| Complexity | Generally simpler | Can be complex |

💡 Note: Understanding the context of the problem can guide you to choose between linear or nonlinear equations for problem-solving.
Strategies to Simplify Learning
Mastering both linear and nonlinear equations can be daunting, but here are some strategies to simplify your learning:
- Visual Learning: Use graphs to visualize equations. This can help in understanding the behavior of different equations.
- Practice with Worksheets: Use worksheets designed for linear and nonlinear equations to reinforce concepts through practical exercises.
- Contextual Learning: Relate equations to real-life problems to understand their applicability.
- Group Study: Engaging with peers can provide new perspectives and solutions.
- Use Technology: Leverage graphing calculators or software to explore how changes in variables affect the graph of an equation.
- Break It Down: For nonlinear equations, break them into smaller, manageable parts, solving step by step.
Wrapping Up

Understanding the fundamental differences between linear and nonlinear equations is vital for your mathematical education. Each type of equation has its unique applications and solving techniques. By recognizing when to apply each, you’ll not only simplify your problem-solving process but also appreciate the beauty of how different mathematical constructs work in harmony to model the world around us. Your journey through math is not just about solving equations; it’s about understanding the logic and patterns that govern our universe.
What’s the difference between linear and nonlinear in real-life contexts?

+
In real-life contexts, linear relationships can be seen in scenarios where there’s a constant rate of change, like the relationship between distance and time in uniform motion. Nonlinear relationships might show up in growth rates, like population growth or decay, or even in financial models where interest rates compound or change over time.
Can I use a calculator for solving all types of equations?

+
Calculators can be quite useful for linear equations where simple algebraic operations are required. However, for nonlinear equations, especially those involving higher degree polynomials or transcendental functions, calculators might not provide exact solutions but can give approximations or help in graphing to visually inspect solutions.
How can I know if an equation is linear or nonlinear?

+
If the equation can be expressed in the form (y = mx + b), where (x) and (y) are variables and (m) and (b) are constants, it’s linear. Any equation where the highest power of the variables is more than one, or where variables are raised to a power in the denominator or involved in other complex operations, is nonlinear.