5 Tips for Solving Arcs and Chords Worksheets
Students often encounter arcs and chords in geometry class, and mastering these concepts can be both challenging and rewarding. From measuring arc lengths to understanding the properties of chords, this topic is fundamental in developing spatial thinking and problem-solving skills. In this guide, we'll explore five effective tips for solving arcs and chords worksheets that can make this mathematical journey a little easier and far more intriguing.
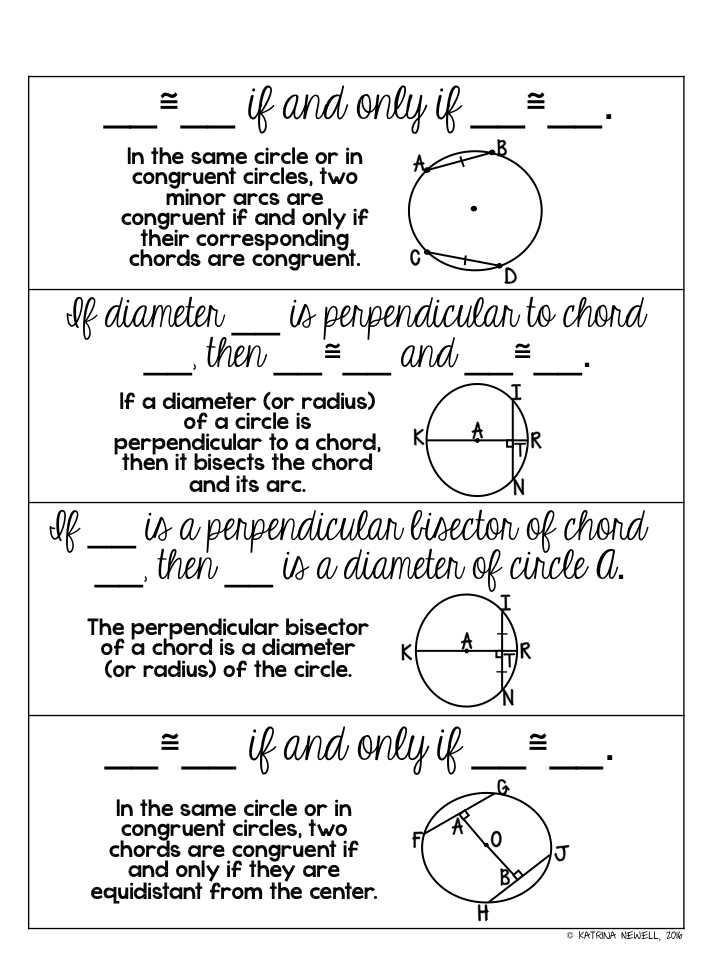
1. Understand the Geometry of Circles

Before diving into complex problems, it's essential to grasp the basic geometry of circles:
- Center: The central point from which all points on the circle are equidistant.
- Radius: The distance from the center to any point on the circle.
- Chord: A line segment connecting two points on the circle.
- Diameter: The longest chord passing through the center.
- Arc: Part of the circumference of the circle.
Knowing these components will help you to visualize and solve problems more efficiently.
2. Apply Central and Inscribed Angle Theorems

Two vital theorems can significantly simplify your approach to arcs and chords:
- Central Angle Theorem: The measure of an arc is equal to the measure of the central angle that intercepts it.
- Inscribed Angle Theorem: The measure of an inscribed angle is half the measure of the intercepted arc.
These theorems can be used to find arc measures, angle measures, and chord lengths:
| Type of Problem | Formula/Concept to Use |
|---|---|
| Finding Arc Length | Arc Length = (angle / 360) × 2πr |
| Inscribed Angle | θ/2 = Arc measure/2 |
| Central Angle | θ = Arc measure |

📐 Note: For complex problems, drawing a diagram can be immensely helpful in understanding the relationship between arcs, chords, and angles.
3. Use the Chord-Chord Power Theorem

When dealing with intersecting chords inside a circle, the Chord-Chord Power Theorem can be a game-changer:
- Products of the lengths of the segments of the chords: If two chords intersect inside a circle, the products of their segments are equal.
This theorem can be used to find unknown lengths when two chords cross each other:
4. Practice Segmenting the Circle

Understanding how to divide a circle into segments can enhance your problem-solving skills:
- Sectors: Wedges formed by radii and an arc.
- Segments: Regions bounded by a chord and an arc.
Practice problems where you have to calculate the area of sectors, segments, or find the arc length of partial circles. Here's an example:
Given a circle with a radius of 5 units, find the area of a sector with a central angle of 60 degrees:
Area = (60/360) * π * r^2 = (1/6) * π * 25 = 4.17 square units approximately.
🔧 Note: Remember, π (pi) is approximately equal to 3.14 for quick calculations, but exact answers require the use of π in equations.
5. Connect Arcs, Chords, and Tangents

Arcs and chords also relate to tangents:
- Tangents to a Circle: A line tangent to a circle at a point forms a 90-degree angle with the radius at that point.
- Tangent-Secant Theorem: If a tangent from an external point touches the circle, and a secant from the same point intersects the circle at two points, then (tangent)^2 = (external part of the secant) * (secant).
These relationships allow for the calculation of tangents' lengths, secant segments, and arc lengths in various geometric scenarios.
In summary, mastering arcs and chords worksheets requires a combination of foundational knowledge, the application of specific geometric theorems, and the ability to visualize spatial relationships. By understanding the basic geometry of circles, using angle theorems, applying the Chord-Chord Power Theorem, practicing segmenting the circle, and connecting arcs, chords, and tangents, you'll become proficient in handling geometry problems involving circles.
What is the difference between an arc and a chord?

+
An arc is part of the circumference of a circle, while a chord is a straight line connecting two points on the circle. Essentially, an arc is curved, whereas a chord is linear.
How can I remember which formulas to use?

+
Create mnemonic devices or memory aids like acronyms. For example, remember “Inscribed Angle” by thinking, “I Arc M O V E,” where I=Inscribed, A=Angle, M=Measure, O=One, V=Half, E=Equation.
Are there common pitfalls when dealing with arcs and chords?

+
Yes, common mistakes include assuming an inscribed angle is equal to an arc’s measure, forgetting to multiply or divide by 2 when using theorems, and confusion between major and minor arcs.
How do tangents relate to arcs and chords?

+
Tangents touch the circle at only one point and are perpendicular to the radius at the point of tangency. They can intersect chords, and their relationships with arcs and chords provide useful problem-solving tools.




