Circle Angle Worksheet: 5 Solutions Revealed

Understanding the Concept of Circle Angles
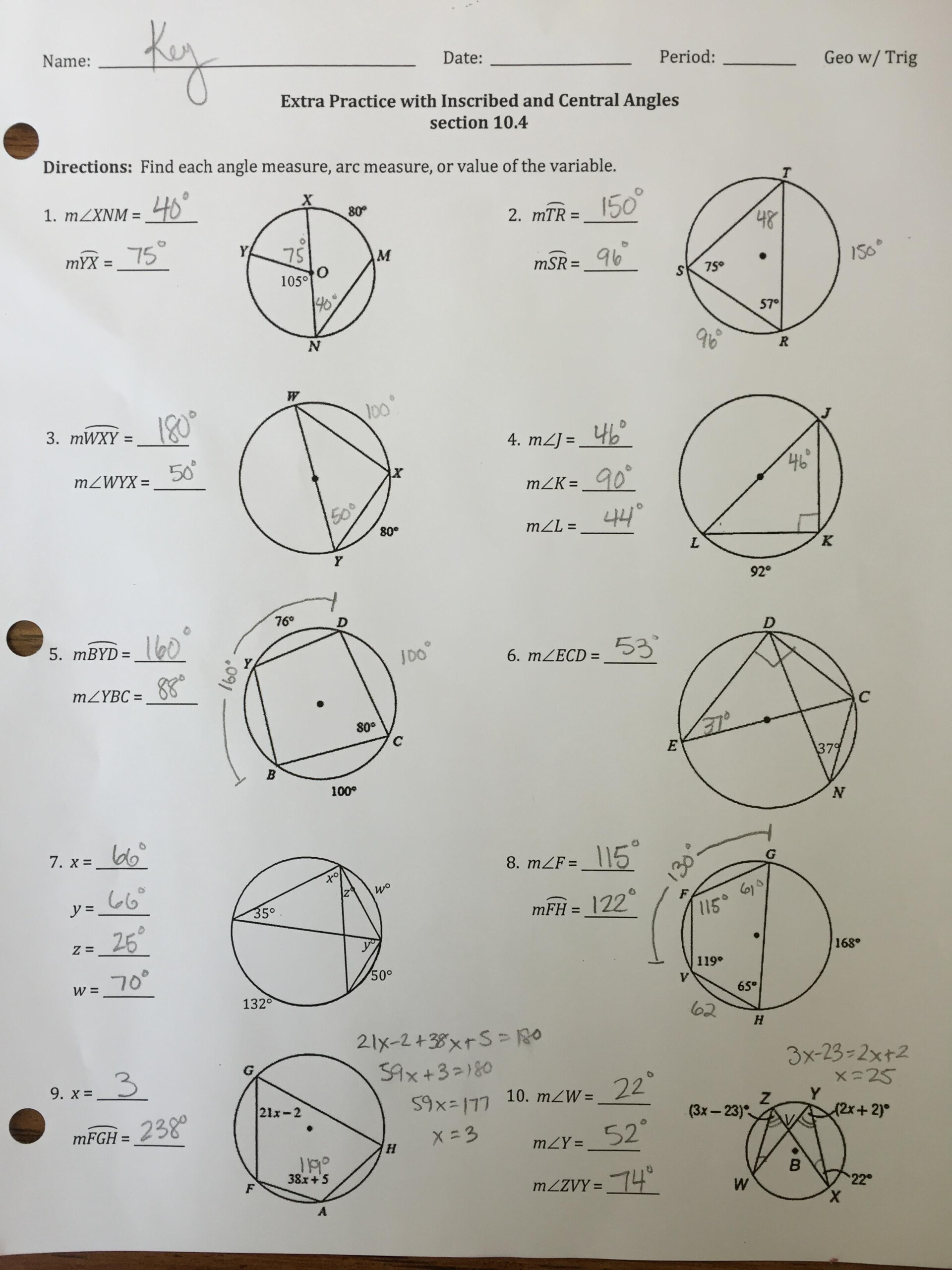
Circles are geometric figures that come with a set of unique properties, especially when it comes to angles. In geometry, understanding the relationship between angles in a circle, especially those subtended by arcs or chords, is crucial for solving various problems. This blog post delves into the different types of angles in a circle, providing a comprehensive guide to tackle related geometry problems.
Central Angles and Inscribed Angles

Central angles are angles whose vertices are at the center of the circle. The measure of a central angle is exactly the same as the measure of the arc it intercepts.
Here is how you can calculate a central angle:
- Identify the two points on the circumference that form the endpoints of the arc.
- Draw lines from each of these points to the center of the circle.
- The angle formed at the center is the central angle.
Inscribed angles, on the other hand, have their vertices on the circumference of the circle. Their measure is half the measure of the arc they intercept.
Angles and Arcs

Angles in circles are closely related to the arcs they subtend:
- An arc subtended by a central angle is a major or minor arc, depending on whether it is greater or less than half the circumference.
- The measure of an inscribed angle is always half the measure of the arc it subtends.
- The sum of the angles of a cyclic quadrilateral (a quadrilateral inscribed in a circle) is always 360 degrees.
Key Formulas for Circle Angles
To understand angles in circles better, here are some key formulas:
| Angle Type | Formula |
|---|---|
| Central Angle | Arc Measure = Central Angle Measure |
| Inscribed Angle | Angle Measure = 1⁄2 * Arc Measure |
| Angles in a cyclic quadrilateral | Sum of Opposite Angles = 180 degrees |
Solutions to Common Circle Angle Problems
Let’s explore five common problems involving circle angles:
Problem 1: Finding an Inscribed Angle
Given an arc length of 40 degrees, find the measure of the inscribed angle intercepting this arc.
To solve:
- Use the formula for an inscribed angle: Angle Measure = 1⁄2 * Arc Measure
- Thus, the inscribed angle would be 1⁄2 * 40 = 20 degrees.
💡 Note: Remember that the inscribed angle is always half the measure of the arc it intercepts.
Problem 2: Central Angle from an Arc

An arc measures 100 degrees. What is the measure of the corresponding central angle?
Solution:
- Central Angle Measure = Arc Measure
- Therefore, the central angle is 100 degrees.
Problem 3: Angle Sum in a Cyclic Quadrilateral

Find the measure of an unknown angle in a cyclic quadrilateral where two known angles are 60 degrees and 70 degrees.
Solution:
- Sum of angles in a cyclic quadrilateral = 360 degrees.
- Sum of given angles = 60 + 70 = 130 degrees.
- Unknown angle = (360 - 130) / 2 = 115 degrees.
Problem 4: Tangent-Secant Angle

Given that a secant and a tangent form an angle of 65 degrees, find the measure of the angle the secant makes with the diameter on the same side as the tangent.
Solution:
- The measure of an angle between a tangent and a chord through the point of tangency is equal to the angle in the alternate segment.
- Therefore, the angle between the secant and the diameter on the same side is 65 degrees.
Problem 5: Angle Between Chords
Two chords intersect within a circle, forming an angle of 50 degrees. Calculate the measure of the arc between these chords’ endpoints.
Solution:
- When two chords intersect, the opposite angles are equal.
- The arc measure between these chords’ endpoints will be twice the intersection angle since the intercepted arc by an inscribed angle is twice the angle itself.
- Therefore, the arc measure is 100 degrees.
In summary, understanding the relationship between angles in circles opens up a wealth of geometric possibilities. By grasping how central angles, inscribed angles, and the properties of arcs and chords relate, one can solve a variety of problems ranging from simple angle calculations to more complex geometric scenarios involving cyclic quadrilaterals and tangents.
What is the difference between a central angle and an inscribed angle?

+
A central angle has its vertex at the center of the circle, and its measure equals the arc it intercepts. An inscribed angle, conversely, has its vertex on the circle’s circumference, and its measure is half the measure of the arc it intercepts.
How do you find the measure of an angle in a cyclic quadrilateral?

+
The sum of opposite angles in a cyclic quadrilateral is always 180 degrees. If you know one pair of opposite angles, you can easily find the other pair.
What happens when a secant and a tangent intersect?

+
When a secant and a tangent intersect outside a circle, the measure of the angle formed is equal to half the difference of the measures of the arcs they intercept.



