Master Fraction Worksheets for 7th Graders Easily

Mastering fraction worksheets in the 7th grade can seem daunting at first, but with the right approach, it can become an engaging and fruitful learning experience. Fractions form the backbone of numerous mathematical concepts, including algebra, measurements, and even geometry, making them an essential part of a student's toolkit. This guide will walk you through how to effectively tackle fraction worksheets, offering strategies that not only help in mastering these worksheets but also in reinforcing your understanding of fractions for everyday problem-solving.
Understanding the Basics of Fractions

Before delving into complex fraction problems, it's crucial to revisit the foundational concepts of fractions:
- Numerator: The number above the line representing the number of parts being considered.
- Denominator: The number below the line indicating the total number of equal parts into which the whole is divided.
Visual Learning

Visual aids can significantly enhance your understanding of fractions:
- Draw pie charts or fraction strips to represent fractions visually.
- Use manipulative like fraction tiles or online fraction calculators to get a hands-on feel for fractions.
Important Concepts to Know:

- Equivalent fractions: Understanding how different fractions can represent the same value, e.g., 1/2, 2/4, and 3/6 are all equivalent.
- Comparing fractions: Learning how to order fractions, which is crucial for operations like addition and subtraction.
- Simplifying fractions: Reducing fractions to their lowest terms to ease computation and comprehension.
Approaching Fraction Worksheets Step-by-Step

Step 1: Identify the Operation

The first step in tackling any fraction problem is to identify what operation you need to perform:
- Adding or subtracting fractions requires a common denominator.
- Multiplying fractions means you multiply the numerators together and the denominators together.
- Dividing fractions involves flipping the second fraction (reciprocal) and then multiplying.
Step 2: Apply the Rules

| Operation | Rule |
|---|---|
| Addition/Subtraction | Find a common denominator, then add or subtract the numerators. |
| Multiplication | Multiply the numerators, then the denominators. |
| Division | Multiply by the reciprocal of the second fraction. |
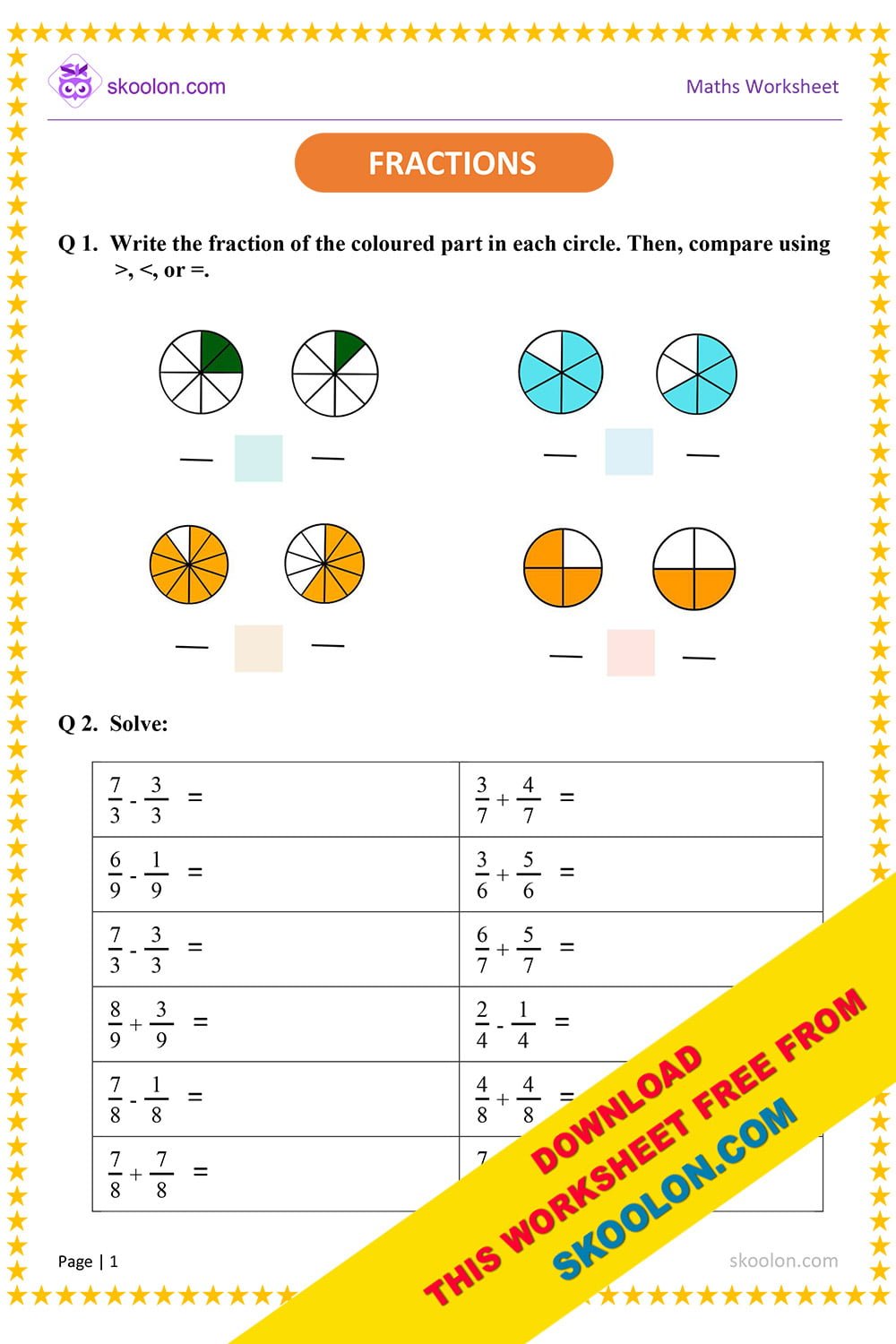
Step 3: Simplify the Answer

Always aim to simplify your fraction to its lowest terms:
- Divide both the numerator and denominator by their greatest common divisor.
- Check if the fraction can be simplified further.
Strategies for Mastering Fraction Worksheets

Regular Practice

Like any skill, mastering fractions requires consistent practice:
- Set aside time each day to work on fraction problems.
- Use a variety of resources to keep practice engaging.
📘 Note: Remember that regular, spaced-out practice is more effective than cramming. Incorporate breaks and review sessions into your routine.
Understanding Word Problems
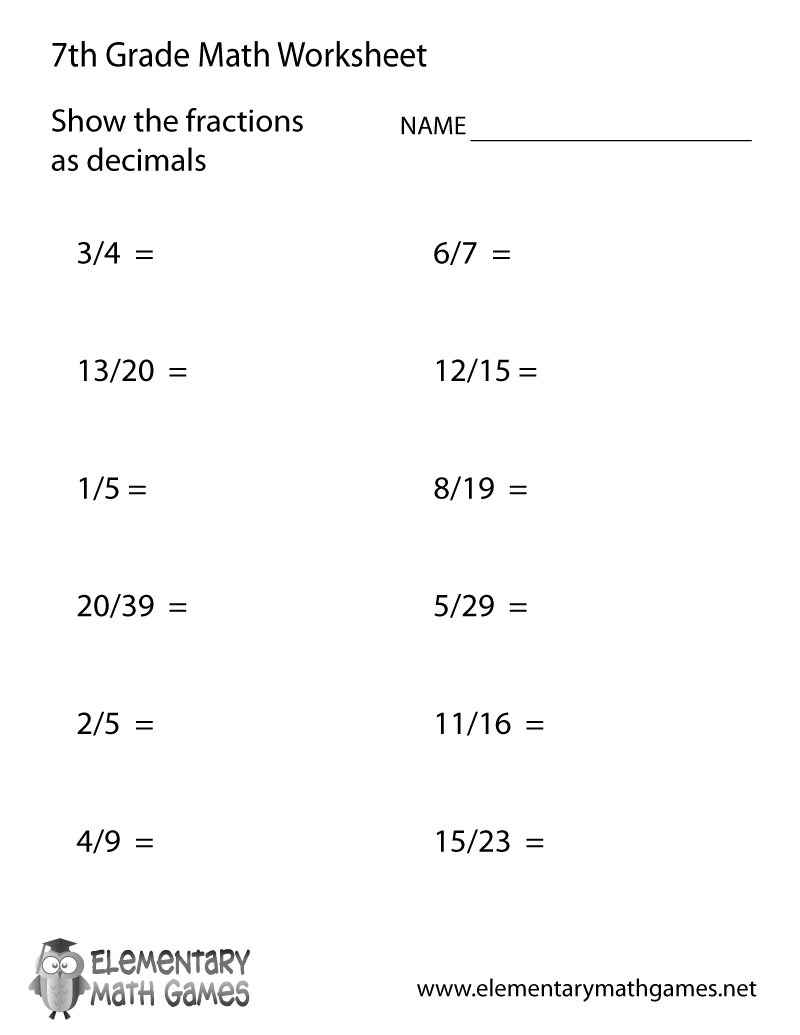
Word problems in fraction worksheets often require a multi-step approach:
- Read the problem carefully to understand what operations are involved.
- Convert the information into mathematical expressions.
- Perform the operations in the correct order.
- Check if your solution fits the context of the problem.
Application in Real Life

Relating fractions to real-life scenarios can make learning more meaningful:
- Cooking recipes often require fraction measurements.
- Sharing items fairly among friends can involve fractions.
Wrapping Up

By following these strategies, you're not just preparing for a worksheet; you're equipping yourself with skills that will serve you in higher math and daily life. Remember to approach each problem with patience, understanding the underlying concepts, and continuously simplifying your results. With persistence and the right tools, fraction worksheets can become less of a chore and more of an opportunity to sharpen your mathematical skills. Keep practicing, keep exploring, and keep enjoying the mathematical journey!
How do I simplify fractions?

+
To simplify a fraction, find the greatest common divisor (GCD) of the numerator and the denominator, and divide both by this number. For example, 6⁄8 can be simplified to 3⁄4 because 6 and 8 both can be divided by 2.
Why do fractions have to have common denominators when adding or subtracting?

+
Having a common denominator allows you to add or subtract the numerators directly because it means you’re working with parts of the same whole.
Can I still use improper fractions in my answers?
+Yes, improper fractions are just as valid as mixed numbers. However, for clarity and sometimes for following instructions, you might need to convert them into mixed numbers or vice versa.