Algebra 2 Parent Functions Worksheet: Transformations Guide

In the realm of Algebra 2, parent functions serve as the cornerstone for understanding how functions behave and can be transformed. They are the most basic versions of different function types, providing a foundation upon which students can build their knowledge of more complex function transformations. Here, we will explore these parent functions and provide a comprehensive guide to understanding and applying transformations to them.
What are Parent Functions?
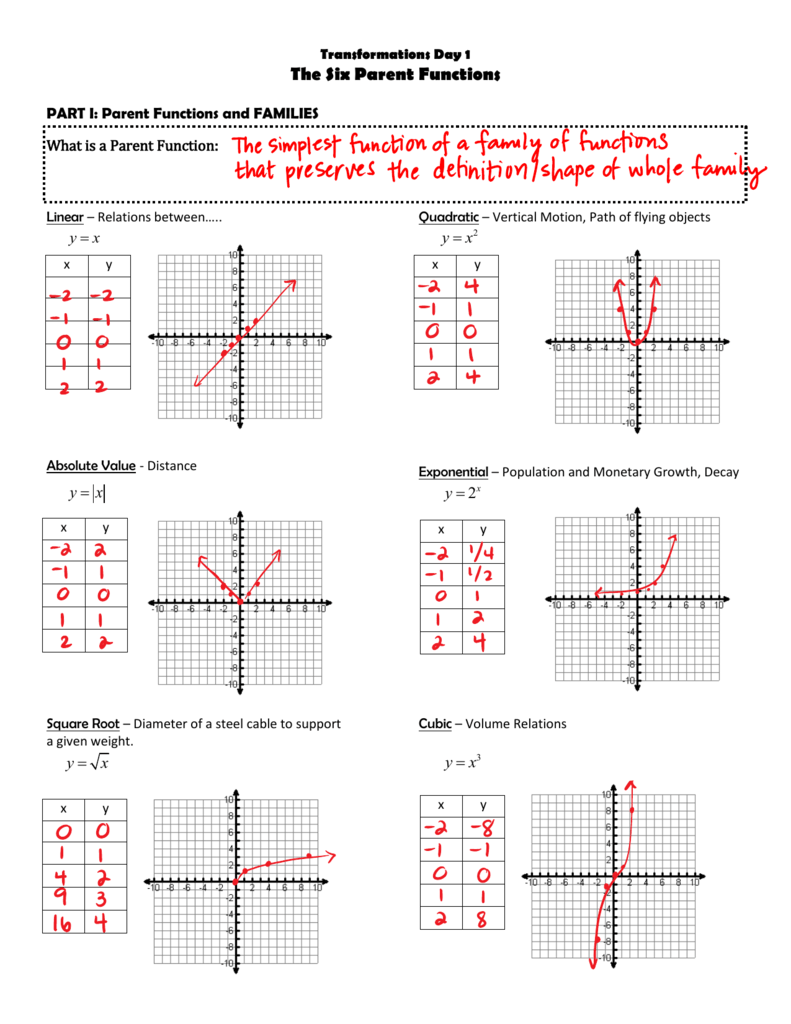
Parent functions in Algebra 2 are the simplest forms of function families. They include linear, quadratic, cubic, exponential, logarithmic, and absolute value functions among others. These functions are represented with the following basic forms:
- Linear: ( f(x) = x )
- Quadratic: ( f(x) = x^2 )
- Cubic: ( f(x) = x^3 )
- Absolute Value: ( f(x) = |x| )
- Exponential: ( f(x) = e^x )
- Logarithmic: ( f(x) = \log_e x )
- Reciprocal: ( f(x) = \frac{1}{x} )
- Square Root: ( f(x) = \sqrt{x} )
How to Identify Parent Functions
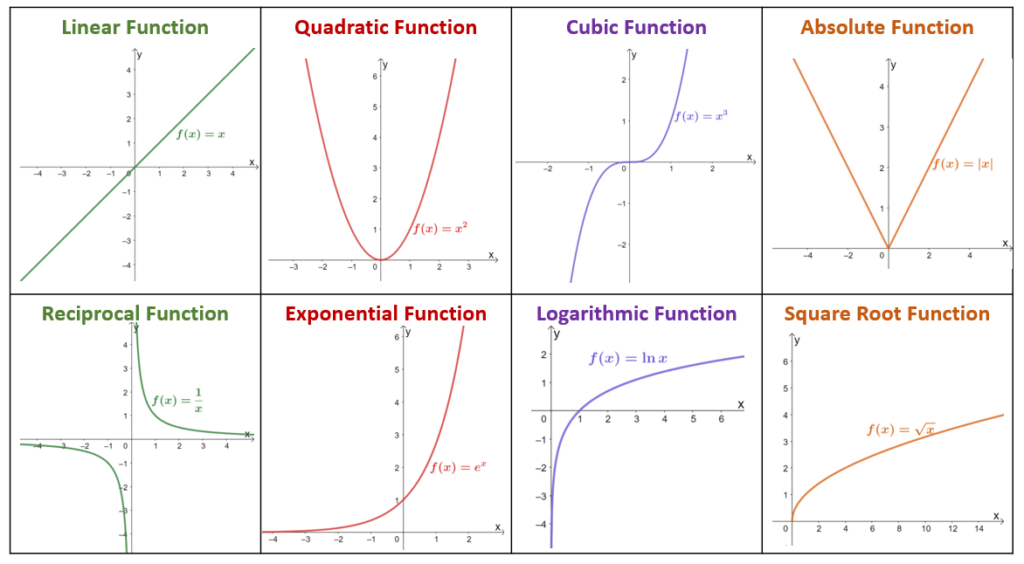
Recognizing parent functions involves understanding their shape, domain, range, and key features:
| Function | Graph Shape | Key Features |
|---|---|---|
| Linear | Straight Line | Slope, no vertical asymptotes |
| Quadratic | Parabola | Vertex, axis of symmetry, opens up or down |
| Cubic | S-Shaped Curve | Point of inflection, at least one real root |
| Absolute Value | V-Shaped | Vertex, symmetry about the y-axis |
| Exponential | Increasing or Decreasing Exponentially | Asymptote, rapid growth/decay |
| Logarithmic | Reflect of Exponential | Vertical asymptote, slow growth |
| Reciprocal | Hyperbola | Two branches, asymptotes |
| Square Root | Half of Parabola | Domain (non-negative x), endpoint at origin |

🌟 Note: Understanding the basic forms of parent functions is crucial for recognizing transformations. Every transformed function will still retain the fundamental characteristics of its parent function.
Function Transformations

Transformations modify a function’s graph in various ways, including vertical and horizontal shifts, reflections, stretches, and compressions. Here’s how each transformation affects a function:
- Vertical Shift: ( f(x) + k ) or ( f(x) - k ) (shift up or down)
- Horizontal Shift: ( f(x + h) ) or ( f(x - h) ) (shift left or right)
- Vertical Stretch: ( af(x) ) (stretches or compresses vertically)
- Horizontal Stretch: ( f(kx) ) (stretches or compresses horizontally)
- Reflection over X-axis: ( -f(x) )
- Reflection over Y-axis: ( f(-x) )
Vertical and Horizontal Shifts

Shifting a function vertically involves adding or subtracting a constant outside the function. This moves the graph up or down:
- ( f(x) + 3 ) will shift the graph of ( f(x) ) up by 3 units.
- ( f(x) - 2 ) will shift the graph down by 2 units.
Horizontal shifts change the x-values by adding or subtracting a constant inside the function:
- ( f(x + 2) ) will shift the graph to the left by 2 units.
- ( f(x - 1) ) will shift the graph to the right by 1 unit.
✨ Note: Horizontal shifts often require careful attention to the direction of the shift, which is the opposite of what you might intuitively expect. Shifting to the left (i.e., towards negative x values) is indicated by a positive constant inside the function, and vice versa.
Stretching and Compressing

Vertical stretching or compressing involves multiplying the function by a scalar factor:
- ( 2f(x) ) will stretch the graph vertically by a factor of 2.
- ( \frac{1}{2}f(x) ) will compress the graph vertically by a factor of 0.5.
Horizontal stretching or compressing is achieved by dividing or multiplying the input by a constant:
- ( f(2x) ) will compress the graph horizontally by a factor of 2.
- ( f(\frac{1}{2}x) ) will stretch the graph horizontally by a factor of 2.
Reflections

Reflecting a function over the x-axis or y-axis changes the function in the following ways:
- ( -f(x) ) reflects the graph over the x-axis.
- ( f(-x) ) reflects the graph over the y-axis.
These transformations are not mutually exclusive and can be combined to form more complex changes in a function's graph. Understanding how these transformations work with parent functions allows for a deeper comprehension of all functions derived from these basics.
Summary

The study of parent functions and their transformations in Algebra 2 is fundamental to understanding the behavior of various types of functions. Through this guide, we’ve explored the basic forms of parent functions, how to identify them, and the impact of various transformations on these functions. By mastering these concepts, students can predict the shape, location, and behavior of functions derived from parent functions, enhancing their ability to work with and analyze more complex mathematical models.
What is the difference between a vertical and horizontal shift?

+
A vertical shift moves the graph of a function up or down by adding or subtracting a constant to the function itself. A horizontal shift, on the other hand, moves the graph left or right by adding or subtracting a constant inside the function argument.
How can you tell if a function has been stretched or compressed?

+
Vertical stretching or compressing is indicated by a scalar factor in front of the function. If the factor is greater than 1, the function is stretched vertically; if it’s between 0 and 1, it’s compressed. Horizontal stretching or compressing involves altering the argument of the function, where a coefficient greater than 1 compresses the function, and less than 1 stretches it.
Can a function undergo multiple transformations at once?

+
Absolutely, functions can undergo multiple transformations simultaneously. The order of transformations can matter, so it’s often best to perform horizontal transformations before vertical ones to avoid confusion.



