5 Easy Ways to Master Adding Unlike Fractions

Mastering the addition of unlike fractions is a skill that not only boosts your mathematical prowess but also has practical applications in everyday life. Whether you're baking, adjusting measurements for home improvement projects, or simply dividing a pizza among friends with different appetites, understanding how to add fractions with different denominators is crucial. Here are five easy ways to become proficient in this fundamental arithmetic operation:
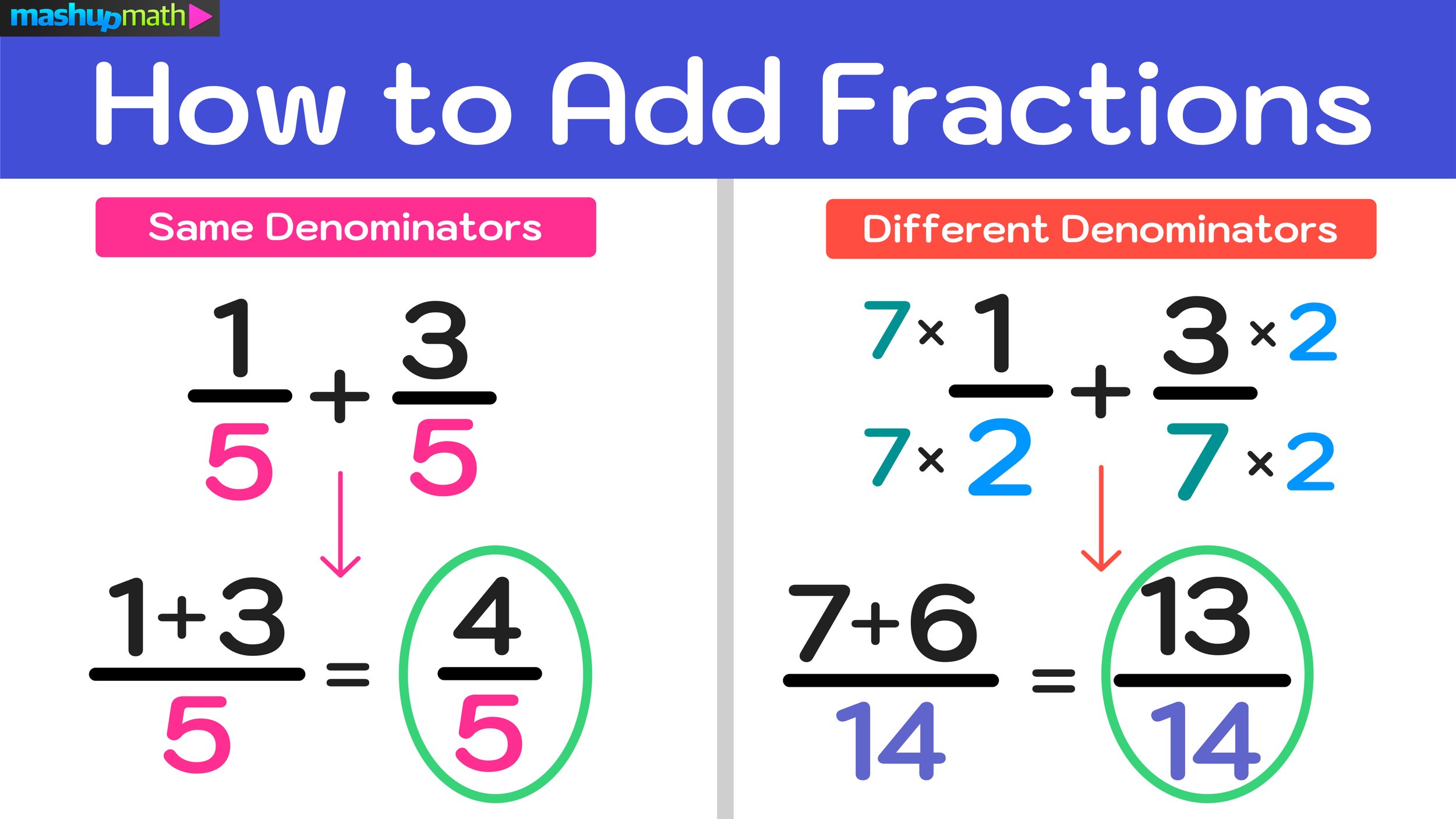
1. Find a Common Denominator

When dealing with unlike fractions, the first step is always to find a common denominator. This is the number that all denominators can divide into evenly. Here are the steps:
- List the multiples of each denominator until you find a common one.
- Identify the smallest (or least) common multiple, which will be your common denominator.
- Convert each fraction so they share this common denominator.
Here's an example:
| Steps | Fraction |
|---|---|
| Denominators | 3 and 4 |
| Multiples of 3 | 3, 6, 9, 12, 15, 18... |
| Multiples of 4 | 4, 8, 12, 16, 20... |
| Common Denominator | 12 |
| Convert Fractions | 1/3 = 4/12 2/4 = 6/12 |
| Sum | 4/12 + 6/12 = 10/12 |
📝 Note: When the common denominator gets very large, it can be cumbersome. Look for the lowest common denominator for ease of calculation.
2. Use the Butterfly Method

The Butterfly Method is a visual technique that helps in finding the sum of unlike fractions without explicitly finding the common denominator:
- Multiply the numerator of the first fraction by the denominator of the second.
- Multiply the numerator of the second fraction by the denominator of the first.
- Multiply the two denominators to get the new denominator.
- Add the results of steps 1 and 2 for the new numerator.
Using 1/3 + 2/4:
- Numerator 1: 1 × 4 = 4
- Numerator 2: 2 × 3 = 6
- Denominator: 3 × 4 = 12
- New Fraction: 4 + 6 = 10 over 12 = 10/12
The Butterfly Method can make the process quicker, especially when dealing with larger numbers or during time-sensitive situations like exams.
3. Practice with Real-Life Scenarios

One of the best ways to master adding unlike fractions is by practicing with real-life scenarios:
- Baking: Recipe adjustments can require you to add or scale ingredients.
- Construction: Converting measurements to work with standard materials.
- Shopping: Comparing items that are on sale with fractions off.
By applying math to tangible situations, the concept of adding unlike fractions becomes more intuitive.
4. Utilize Educational Tools

Various educational tools can aid in mastering adding unlike fractions:
- Online calculators: Use calculators that show steps to understand the process.
- Mobile apps: Apps like Mathway, Photomath, or Khan Academy can offer interactive lessons.
- Worksheets: Free or paid printables can provide structured practice.
🔬 Note: Educational tools are a great supplement, but understanding the math behind the process is crucial for long-term mastery.
5. Understand Equivalent Fractions

Being able to convert fractions to their equivalent forms is fundamental in adding unlike fractions:
- Multiplying or dividing both the numerator and the denominator by the same number keeps the value of the fraction the same.
- Knowing how to create equivalent fractions helps in finding a common denominator or simply solving addition problems directly.
Here's how equivalent fractions help:
- 1/2 can become 2/4, 3/6, or 4/8.
- 3/4 can become 6/8, 9/12, or 12/16.
By understanding how fractions relate to each other through equivalence, you can more easily find a common ground for adding them together.
Whether you're a student, a professional, or someone dealing with day-to-day numerical challenges, mastering the addition of unlike fractions can be both fun and practical. By incorporating these five methods into your learning, you'll gain not only confidence but also proficiency in this essential math skill. The key is consistent practice, a bit of creativity in application, and utilizing all available resources to understand and apply the concept in various contexts.
Why is it important to add unlike fractions?

+
Adding unlike fractions is crucial in many practical scenarios like adjusting ingredient quantities in cooking, converting measurements for sewing or construction, and understanding financial ratios or discounts. It helps in making accurate calculations in various life situations.
How can I quickly find the least common denominator (LCD)?

+
One quick way to find the LCD is by using the prime factorization method. Factorize each denominator into its prime factors, then choose the highest power of each prime factor present, and multiply these together to get the LCD. Alternatively, software tools or online calculators can quickly provide the LCD.
Can I use a calculator to add unlike fractions?
+
Yes, modern calculators and many online calculators can handle adding unlike fractions. However, understanding the manual process is beneficial for grasping the concept and for situations where technology is not available.
What are some common mistakes when adding unlike fractions?

+
Common mistakes include not converting to a common denominator, mixing up the numerators and denominators when converting, and forgetting to simplify the final result. Another frequent error is adding the denominators instead of finding a common one.
What are some advanced techniques for adding fractions?

+
Advanced techniques include using the LCD (Least Common Denominator), the Butterfly Method, or even the Cross Multiplication Method for simplifying the process of finding a common denominator or performing the addition directly.



