Master Rational Expressions: Add, Subtract, Worksheet Included

Understanding Rational Expressions: A Comprehensive Guide
Rational expressions are a fundamental part of algebra and they often prove to be a challenging concept for students. Similar to fractions, rational expressions involve a numerator over a denominator, where both can be polynomials. In this in-depth exploration, we will delve into the intricacies of working with rational expressions, particularly focusing on addition and subtraction, complete with practical examples and a downloadable worksheet to hone your skills.
What Are Rational Expressions?

A rational expression is defined as the ratio of two polynomials. For instance, \frac{2x + 1}{3x - 4} is a rational expression, where 2x + 1 is the numerator, and 3x - 4 is the denominator. Before we proceed to the operations like addition and subtraction, it's vital to know a few foundational rules:
- Reduced Forms: Rational expressions are typically simplified by factoring both the numerator and the denominator, canceling out common factors. Remember, you cannot cancel terms within sums or differences; only factors common to entire expressions.
- Illegal Values: If the denominator is zero, the rational expression is undefined. Identifying and excluding these values from the domain is a crucial step.
Adding and Subtracting Rational Expressions

Step-by-Step Addition

Adding rational expressions mirrors the process of adding fractions:
- Find a Common Denominator: Determine the least common multiple (LCM) of the denominators.
- Rewrite Each Fraction: If necessary, convert each expression to have the common denominator.
- Add the Numerators: Combine the numerators over this common denominator.
- Simplify: Factor if possible and reduce the resulting expression.
Example: Consider \frac{1}{x} + \frac{2}{x + 3}.
- The LCM of x and x + 3 is x(x + 3).
- We can rewrite \frac{1}{x} + \frac{2}{x + 3} as \frac{1(x + 3)}{x(x + 3)} + \frac{2x}{x(x + 3)}.
- Adding the numerators gives us \frac{(x + 3) + 2x}{x(x + 3)} = \frac{3x + 3}{x(x + 3)}.
- Finally, factor and simplify: \frac{3(x + 1)}{x(x + 3)}.
Subtracting Rational Expressions

Subtracting follows the same steps as addition, with one key difference:
- Instead of adding numerators, we subtract them.
Example: Consider \frac{3}{2x - 1} - \frac{1}{2x + 2}.
- The common denominator here is (2x - 1)(2x + 2).
- Rewrite as \frac{3(2x + 2) - 1(2x - 1)}{(2x - 1)(2x + 2)}.
- Perform the subtraction in the numerator: \frac{6x + 6 - 2x + 1}{(2x - 1)(2x + 2)} = \frac{4x + 7}{(2x - 1)(2x + 2)}.
- And this is your simplified rational expression.
Additional Notes:
🔔 Note: Always check the final simplified expression to ensure no factor cancels out a term that should not have been canceled. Remember, variables represent numbers; what holds true for one value might not for another.
Understanding the Domain of Rational Expressions

After performing operations on rational expressions, it’s essential to determine the domain of the resulting expression. This ensures we exclude values that would make the denominator zero:
- Set the denominator equal to zero and solve for the variable.
- Exclude these values from the domain of your expression.
Example: Given the expression \frac{x - 3}{x^2 - 4},
- Setting the denominator equal to zero gives us x^2 - 4 = 0 or (x - 2)(x + 2) = 0.
- Solving gives x = 2 or x = -2.
- Thus, the domain is all real numbers except x = 2 and x = -2.
Practical Exercises and Worksheet
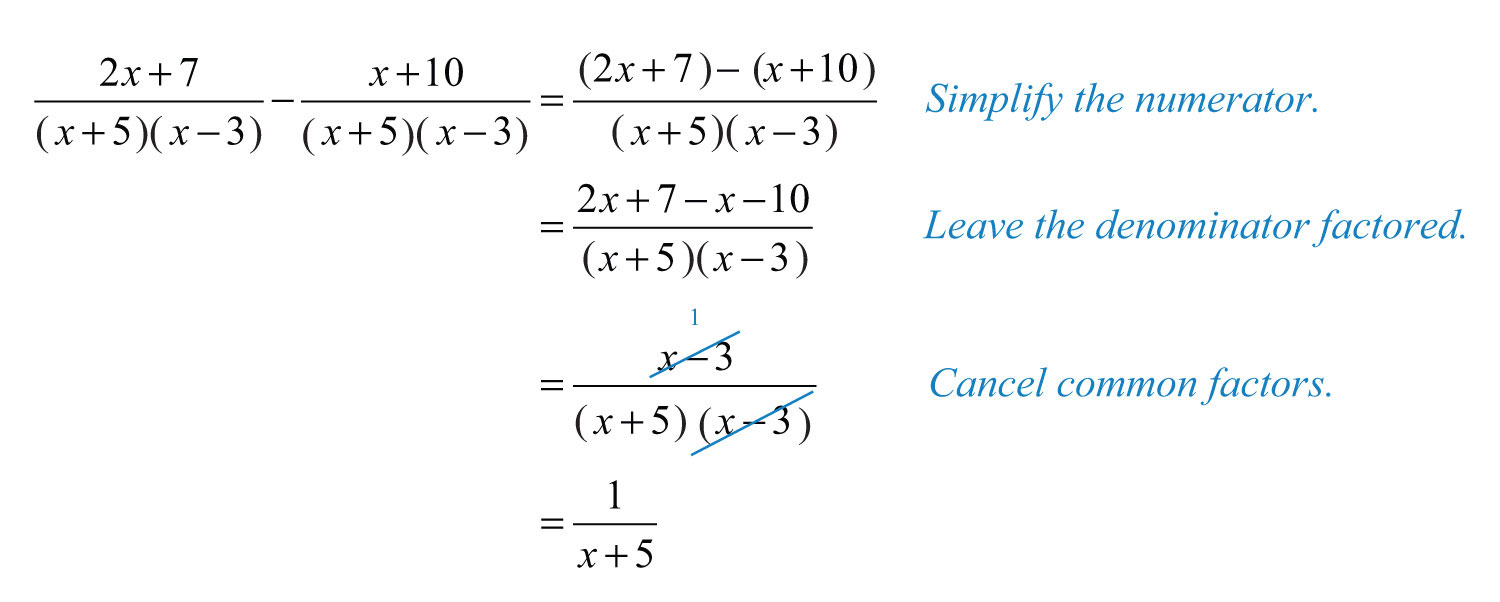
We've included a comprehensive worksheet that provides exercises on adding and subtracting rational expressions. This worksheet is designed to:
- Promote understanding through repetitive practice.
- Encourage you to identify common denominators and simplify expressions correctly.
- Challenge you with a mix of basic to advanced problems.
📚 Note: The worksheet includes problems where you must also determine the domain of the resulting expression.
Final Thoughts

In our journey through rational expressions, we’ve tackled their basic structure, how to add and subtract them, and even dipped our toes into the domain of resulting expressions. The key to mastering rational expressions is consistent practice and a firm grasp on polynomial factorization and finding common denominators. This post serves as a stepping stone towards a deeper understanding of algebra, a fundamental skill for advanced mathematics and real-world problem-solving.
Why do I need to find a common denominator when adding or subtracting rational expressions?

+
To add or subtract fractions or rational expressions, all denominators must be the same. This common denominator allows the numerators to be combined effectively over one expression.
What happens if the numerator and the denominator have a common factor?

+
If there’s a common factor in both numerator and denominator, it can be simplified. However, ensure you are canceling the entire factor, not just terms within polynomials.
How do I check my work when simplifying rational expressions?

+
After simplifying, check for errors by expanding the simplified expression back to its original form or by substituting a value (not making the denominator zero) to confirm equivalence.
Can rational expressions have negative exponents?

+
In rational expressions, negative exponents can be rewritten in their reciprocal form. For example, (x^{-2}) can be expressed as (\frac{1}{x^2}) in the numerator.
Is it possible to have an imaginary solution when simplifying rational expressions?
+
While simplifying rational expressions, you might encounter imaginary numbers if you take the square root of a negative number during the simplification process. However, this does not mean the expression itself involves imaginary numbers inherently.



