5 Essential Tips for Mastering Radicals Addition and Subtraction

Working with radicals, those mathematical expressions that feature a root symbol, can seem daunting at first, but with the right strategies and practice, they become manageable. Whether you're a student preparing for math exams or an enthusiast looking to better understand algebra, mastering radicals addition and subtraction is key to solving many mathematical problems. This blog post outlines 5 Essential Tips for effectively handling these operations, making your journey through algebra smoother and more successful.
1. Simplify Radicals Before Adding or Subtracting


Before you can add or subtract radicals, they need to be in their simplest form. Here's how to approach simplification:
- Prime Factorization: Break down the number inside the radical into its prime factors to simplify it.
- Perfect Squares: Look for factors that are perfect squares, as you can take their square roots out of the radical.
- Multiplication: If the radicals contain different numbers, multiply them and then simplify.
Here’s an example:
Given √72 + √128:
- √72 = √(36 * 2) = √36 * √2 = 6√2
- √128 = √(64 * 2) = √64 * √2 = 8√2
Now, add them:
6√2 + 8√2 = (6 + 8)√2 = 14√2
🔎 Note: Not all radicals can be simplified to the same radical term. You can only add or subtract like radicals.
2. Use the Distributive Property

The distributive property allows you to distribute a factor across radicals:
- If you have a term with a common factor outside the radical, you can distribute it to simplify the addition or subtraction.
Example:
4√3 + 6√3
You can factor out √3:
(4 + 6)√3 = 10√3
3. Combine Like Terms

Just like combining like terms in basic algebra, radicals with the same radicand (the number inside the root) can be combined:
- Add or subtract the coefficients outside the radicals.
Here’s an example:
2√7 + 5√7 - √7
Combining the like terms:
(2 + 5 - 1)√7 = 6√7
4. Recognize When Radicals Can't Be Simplified or Combined

There will be instances when you can't add or subtract radicals:
- If the radicals don't share the same radicand or if they're already in their simplest form.
Example:
√2 + √3
These terms can't be added or subtracted further because the radicands are different, and they can't be simplified.
5. Practice and Understand Each Step

Consistent practice is crucial:
- Work through various problems to understand when each tip is applicable.
- Practice combining radicals in different contexts, like expressions with variables.
The key to mastering radicals is understanding each step, from simplification to recognizing when operations can or cannot be performed:
In summary, mastering the addition and subtraction of radicals involves:
- Simplifying radicals to their simplest form before combining.
- Using the distributive property when appropriate.
- Combining like terms where possible.
- Recognizing when radicals can't be simplified or combined.
- Engaging in regular practice to hone your skills.
With these tips in mind, algebra becomes less of a hurdle and more of an intriguing challenge. Now, let's dive into some frequently asked questions that might help clear up any remaining uncertainties about working with radicals.
What are radicals?
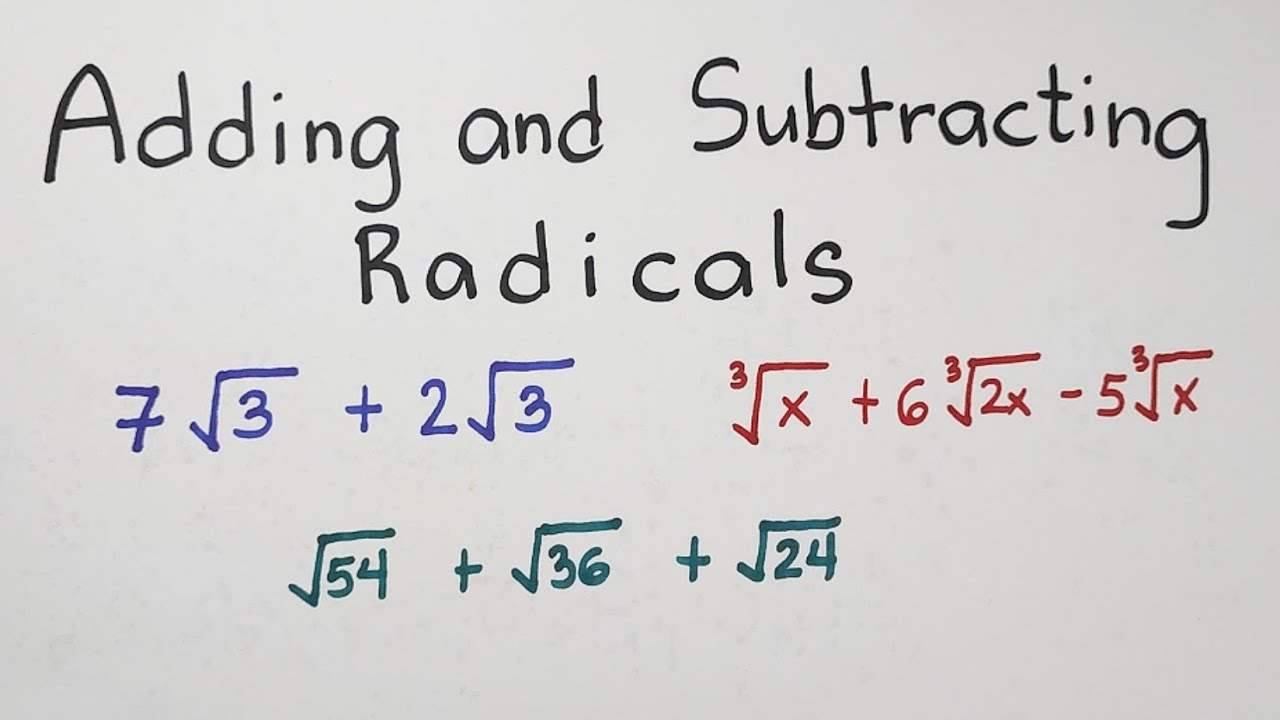
+
Radicals are expressions involving roots, typically represented by the square root symbol (√). They can also involve other roots like cube roots or fourth roots.
Why can’t we add different radicals?

+
Radicals represent different sets of values; thus, you can only combine them when they have the same radicand or can be simplified to have the same radicand. Otherwise, they are like terms with different variables, which can’t be combined directly.
Is there a method to check if simplification is possible?

+
Yes, one can use the prime factorization method. If there are common factors that can be removed from the radicand (which must be perfect squares, cubes, etc.), simplification is possible.
Can I add variables inside radicals?

+
If the variables are like terms, then you can simplify and combine them similar to how you do with numbers. However, if the radicands contain variables with different degrees, they can’t be added or subtracted in their current form.
What to do when the radical’s radicand is not a perfect square?

+
If the radicand isn’t a perfect square, look for factors within the radicand that are perfect squares, pull these out, and then proceed with any possible addition or subtraction.