Master Rate of Change with Our Interactive Worksheet

Rate of change is a fundamental concept in mathematics, particularly in algebra and calculus, and it finds numerous applications in real-life scenarios, from analyzing the speed of a moving object to understanding the growth rate of bacteria. Our interactive worksheet on rate of change is designed to help you master this essential topic through engaging, practical exercises and step-by-step guidance. Let's dive into how you can fully utilize this tool to grasp the concept comprehensively.
Understanding Rate of Change


At its core, the rate of change describes how one variable changes with respect to another. It’s often represented as the slope of a line or a curve in mathematical graphs. Here’s a quick rundown on what you need to understand:
- Slope: The change in the y-variable divided by the change in the x-variable, often represented as Δy/Δx.
- Speed: In physics, the rate of change of distance with respect to time is speed.
- Average vs. Instantaneous Rate of Change: Understand how they differ in their application.
Navigating Our Interactive Worksheet

Here’s how you can make the most of our interactive worksheet:
Exercise Types

Our worksheet includes several types of exercises to cater to different learning styles:
- Multiple Choice Questions: Test your basic understanding and application of rate of change.
- Graph-based Problems: Visually interpret and calculate rates of change from graphs.
- Word Problems: Apply concepts to real-life scenarios for a deeper understanding.
- Instant Feedback: Receive immediate feedback on your solutions, helping to correct mistakes on the spot.
Step-by-Step Guidance

The interactive nature of the worksheet provides step-by-step guidance:
- Identify the variables involved.
- Determine if you’re looking for an average or instantaneous rate of change.
- Apply the formula or interpret the graph appropriately.
- Enter your answer for immediate feedback.
💡 Note: When working with graphs, remember to use the grid to approximate values if exact coordinates are not provided.
Challenging Scenarios
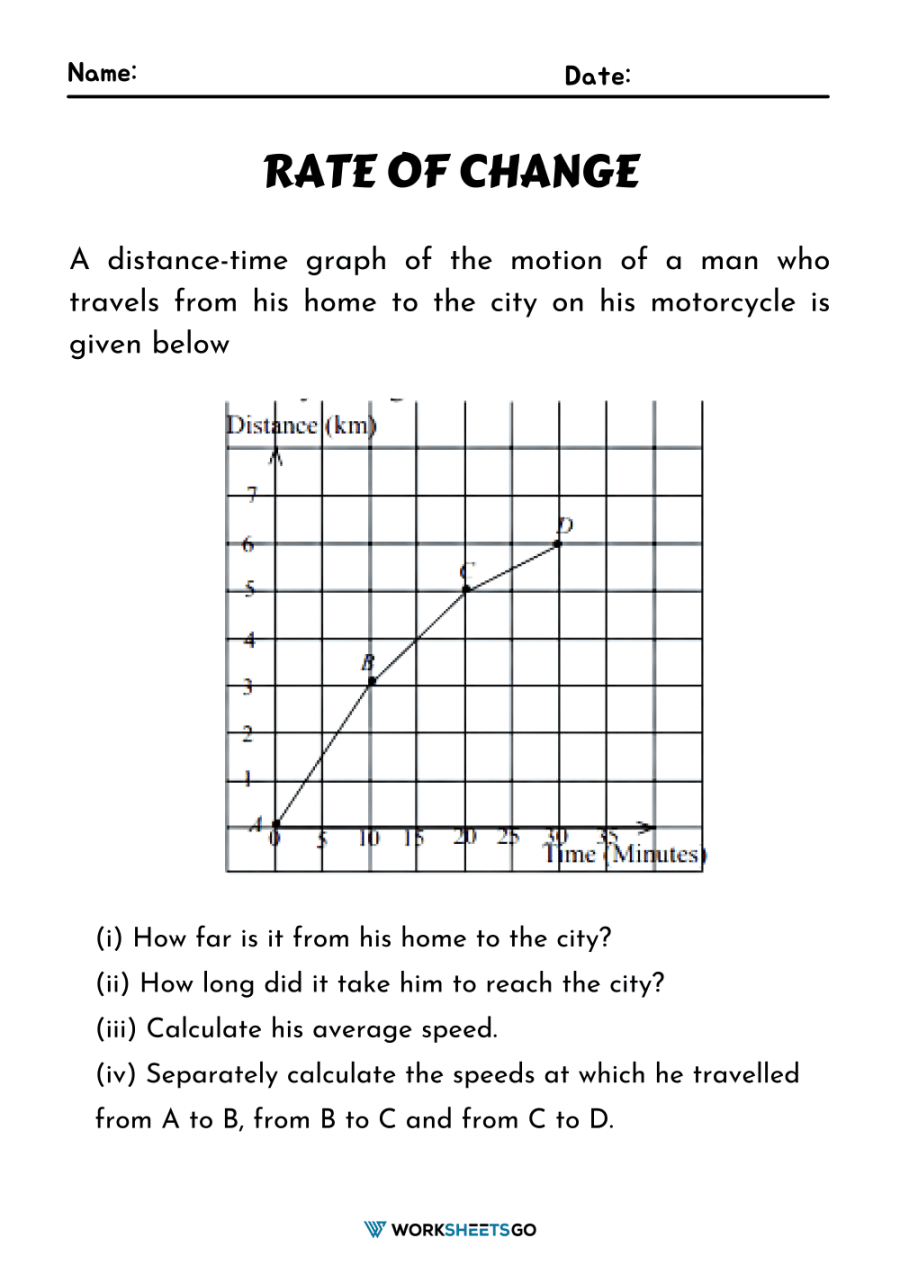
To help you master rate of change, we’ve included scenarios where the rate changes or where multiple rates are at play:
- Calculating the rate of change over different intervals.
- Understanding rates of change in complex functions or piecewise functions.
Tools for Learning

Interactive elements in our worksheet include:
- Drag-and-drop: Place points on a graph to see how rates of change alter.
- Calculators: Tools to calculate rates of change for given data sets.
- Explanation Sliders: Reveal explanations as you progress through each problem.
Mastery Tips

Here are some strategies to truly master rate of change:
- Practice Regularly: Regular practice reinforces concepts.
- Understand the Concept: Don’t just memorize formulas; understand the concept behind the math.
- Relate to Real-life: Think about how the rate of change applies in everyday situations.
- Use Visual Aids: Graphs are your friends. Visualize the rates.
📝 Note: Sometimes, the rate of change can be negative, indicating a decrease, so be alert to the direction of change.
In Summary

We’ve explored the fundamental principles of rate of change and how our interactive worksheet can aid in your learning journey. By engaging with a variety of problems, you can develop a deeper understanding of how rates of change manifest in various contexts, from simple linear equations to more complex functions. Remember, mastery comes not just from solving problems but from understanding the underlying concepts and their real-life implications. Use the step-by-step guidance, receive immediate feedback, and push yourself through challenging scenarios to truly grasp this vital mathematical concept.
What is the difference between average and instantaneous rate of change?

+
The average rate of change measures how a function changes over an interval or set of data points, calculated by the change in y-value divided by the change in x-value. In contrast, the instantaneous rate of change represents the slope of the tangent line at a specific point on a curve, showing the rate of change at that exact moment. This is often found using derivatives in calculus.
How do I know if the rate of change is positive or negative?

+
If the slope of the line or curve is positive, the rate of change is positive, indicating that the y-variable is increasing as the x-variable increases. A negative slope means the rate of change is negative, indicating a decrease in the y-variable as the x-variable increases.
Can rate of change be zero?

+
Yes, a rate of change can be zero, indicating that there is no change in the y-variable with respect to the x-variable over a given interval or at a specific point. This happens when the function is horizontal or at its local maxima or minima.