Master Triangle Angles with Our Free Worksheet!
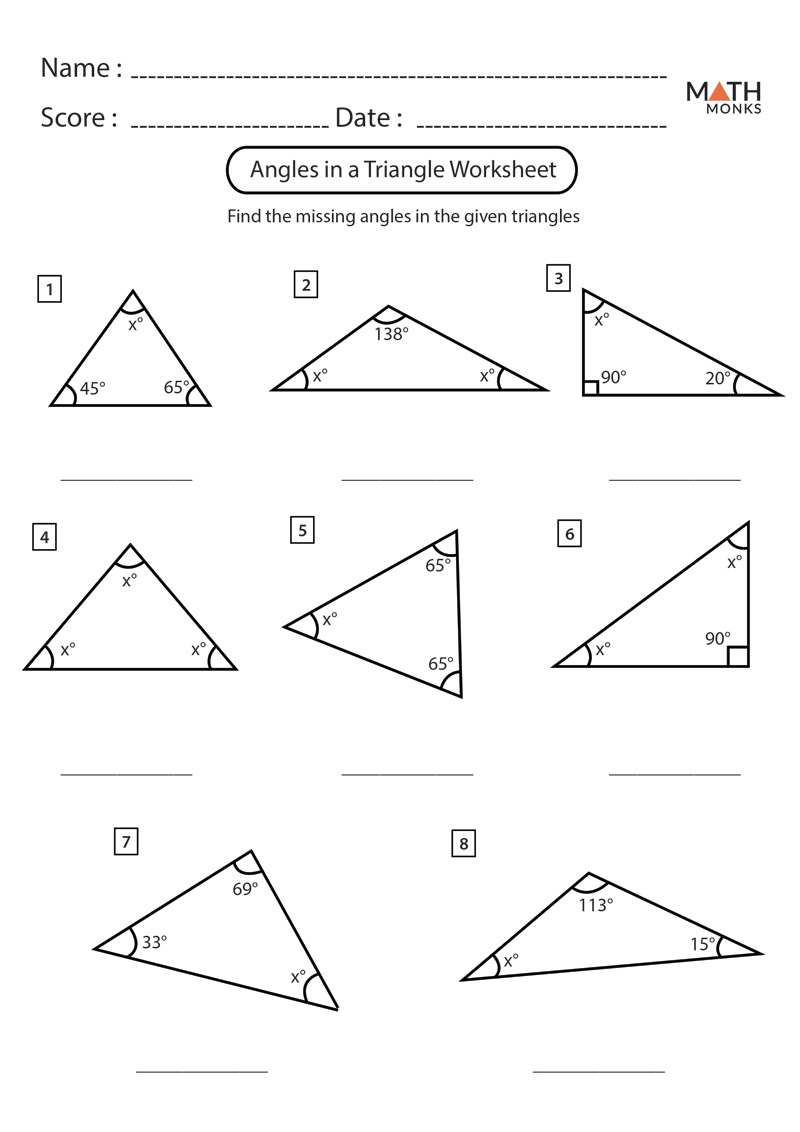
If you've ever grappled with the intricacies of triangle angles, then this blog post is your golden ticket to mastering them! Triangles are the simplest polygon, yet they hold a fascinating array of properties, particularly when it comes to the sum of their interior angles. With the free worksheet we've prepared, you'll not only learn how to calculate these angles but also understand why they behave the way they do. Let's dive into the world of triangles, explore their angles, and understand how this knowledge applies beyond just solving problems in math class.
Understanding Triangle Angles

Before we dive into the worksheet, let's cover the basics. In any triangle, the sum of the interior angles is always 180°. This rule is fundamental, making triangles predictable in a geometric sense. Here's how you can think about it:
- The angles inside a triangle add up to 180°.
- Each angle in an equilateral triangle is 60° because all angles are equal.
- In isosceles triangles, two angles are equal, making the other angle easily calculable.
💡 Note: This rule applies to all triangles, regardless of their shape or size.
Identifying Types of Triangles by Angles

Understanding the classification of triangles by their angles can give you a head start in solving for unknowns:
- Acute Triangle: All angles are less than 90°.
- Right Triangle: Exactly one angle is 90° (right angle).
- Obtuse Triangle: One angle is greater than 90° but less than 180°.
Knowing these types helps in using the right strategies to find angle measures.
Steps to Calculate Triangle Angles

Here are the steps you can follow to determine the angles of a triangle:
- Identify Known Angles: Start by noting any angles you already know.
- Use the Sum Rule: Remember, all angles must add up to 180°.
- Set Up an Equation: Use algebra to solve for the unknown angle. For example, if you know two angles, you can say, "Angle 1 + Angle 2 + Angle 3 = 180°." Let x be the unknown angle, then rearrange to solve for x.
- Solve and Check: After finding the unknown angle, verify your solution by ensuring all angles sum to 180°.
| Triangle Type | Properties |
|---|---|
| Equilateral | All angles are 60° |
| Isosceles | Two equal angles |
| Scalene | All angles are different |

🔍 Note: You can also use the exterior angle theorem or properties of parallel lines when dealing with more complex problems.
The Worksheet

We've created a free worksheet that will help you practice these concepts with real-world examples and problems. Here’s what you’ll find:
- Various types of triangles with some angles given, asking you to find the others.
- Exercises on calculating angles in different scenarios, like when one angle bisects another.
- Word problems where triangle angle calculations are necessary to solve real-life situations.
Using the Worksheet Effectively

Here are some tips for making the most out of your practice:
- Start with the simpler problems to warm up.
- Use a calculator for precision but aim to understand why your answer makes sense.
- Check your work by adding all angles to ensure they equal 180°.
- Work through the problems at a pace that allows for learning, not just completing the task.
Remember, practice isn't just about solving; it's about understanding why triangles behave the way they do.
By now, you should feel more confident about tackling triangle angles, thanks to our detailed explanation and free worksheet. Triangles are not just shapes on paper; they help in understanding everything from architecture to engineering and beyond. Every time you calculate an angle, you're engaging with the logic and beauty of mathematics, learning how simple rules govern complex structures. Remember, every angle is part of a bigger picture, and now, with this knowledge, you can see that picture more clearly. Keep practicing, keep questioning, and keep exploring the fascinating world of geometry!
What are the properties of triangles?

+
Triangles have several key properties: the sum of the interior angles is 180°, the exterior angle of a triangle is equal to the sum of the opposite two interior angles, and for isosceles triangles, the base angles are equal. Additionally, triangles can be classified by their sides or angles, which affects their properties.
Why do triangles always have angles summing to 180°?

+
Due to the way triangles are defined in Euclidean geometry, when you extend the sides of a triangle, you create parallel lines, and the angles formed between these parallel lines and the triangle’s angles add up to a straight line (180°), which leads to the conclusion that the angles in a triangle must sum to 180°.
How can I use the worksheet for better understanding?

+
Use the worksheet by starting with the easier exercises to build confidence, then tackle more complex problems. Check your answers, use a calculator for accuracy, and think about why each angle is what it is. Remember to review your work to ensure the angles sum correctly.