Linear Equation Slope Intercept Form Worksheet Mastery

Understanding how to master the slope intercept form of linear equations is crucial for anyone diving into the fascinating world of algebra. This specific form, represented as y = mx + b, where m stands for the slope and b the y-intercept, is fundamental not just for plotting lines but for understanding various applications in science, economics, and daily life scenarios where linear relationships exist. In this extensive guide, we'll delve into how to use, interpret, and master the slope intercept form through structured worksheets that offer both practice and understanding.
Why Use Slope Intercept Form?
The slope intercept form provides a straightforward way to:
- Determine the slope of a line at a glance.
- Identify where the line intersects the y-axis.
- Easily plot lines on a graph without performing complex calculations.
- Solve for y when x values are given or vice versa.
Understanding the Slope

The slope (m) in y = mx + b represents how much y changes for every one-unit increase in x. Here’s what different slopes mean:
- Positive Slope: The line rises from left to right, indicating a direct relationship between the variables.
- Negative Slope: The line descends from left to right, showing an inverse relationship.
- Zero Slope: A horizontal line, y remains constant as x changes.
- Undefined Slope: A vertical line, where x is always the same, and y can be any value.
🔍 Note: Remember, the slope is also the tangent of the angle the line makes with the x-axis.
Mastering the y-Intercept

The y-intercept (b) is the point where the line crosses the y-axis. It represents the value of y when x is zero. Here’s how to interpret it:
- If the y-intercept is positive, the line crosses above the origin.
- If it’s negative, the line crosses below the origin.
- A y-intercept of zero means the line passes through the origin (0,0).
Worksheet Structure for Mastering Slope Intercept Form

To truly master the concept, a structured approach is essential:
1. Basic Conversion

Start with equations in different forms and convert them into slope-intercept form:
| Equation | Converted Form |
|---|---|
| 2x + y = 6 | y = -2x + 6 |
| x - y = 0 | y = x |

2. Slope Identification

Provide equations and ask to identify the slope:
- y = 3x - 1 → Slope: 3
- y = -2/3x + 4 → Slope: -2⁄3
3. y-Intercept Identification

Find the y-intercept from given equations:
- y = x + 5 → y-Intercept: 5
- y = -x - 1 → y-Intercept: -1
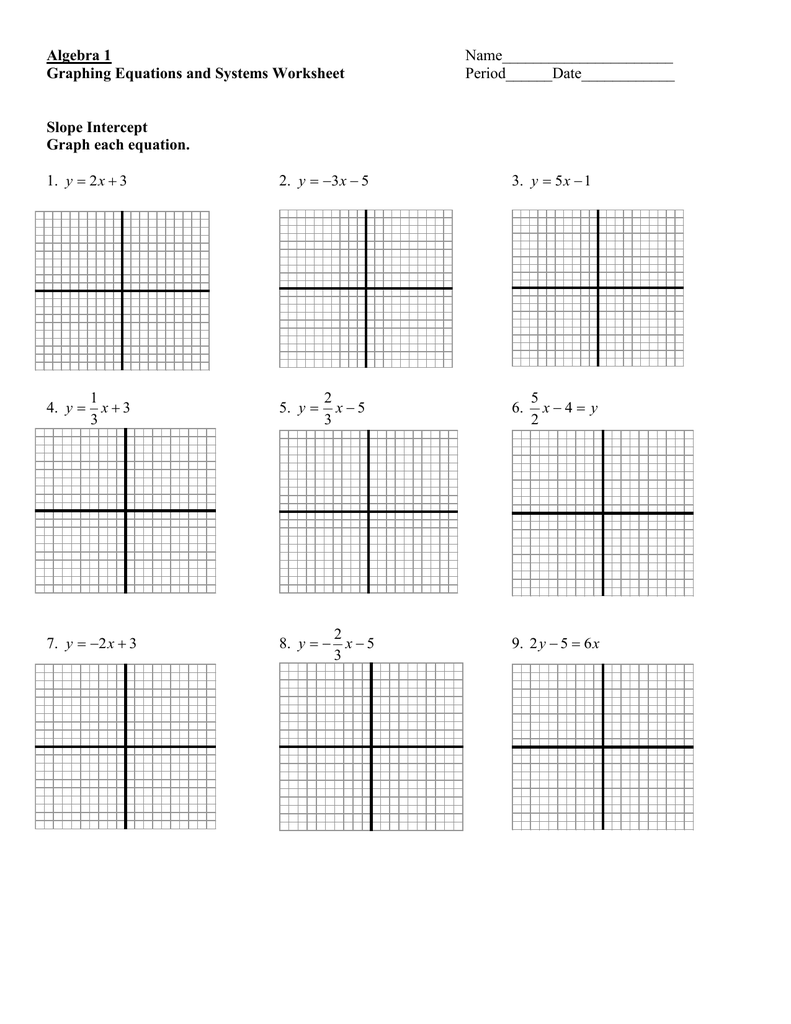
4. Graphing

Plot lines on a graph given in slope intercept form:
- y = 2x - 3
- y = -x + 1
5. Problem-Solving

Use real-world problems to understand applications:
- If a taxi fare starts at 3 and increases by 1.50 per mile, write the equation in slope intercept form.
- Determine the slope and y-intercept of a line that represents a company’s profit if its revenue grows by 2% per month from a starting point of $50,000.
💡 Note: Use different types of problems to cover all aspects of application.
6. Advanced Concepts

Incorporate exercises to practice finding the equation of a line given:
- Two points on the line.
- Slope and one point on the line.
Incorporating these practice areas ensures a thorough understanding of the slope intercept form, enhancing both mathematical and analytical skills.
In wrapping up, mastering the slope intercept form of linear equations goes beyond mere number crunching. It opens up a world of possibilities where you can model relationships, predict outcomes, and make data-driven decisions in various fields. From graphing simple lines to solving real-world problems, the journey through these worksheets helps solidify the foundational concepts of algebra. By continually engaging with these exercises, students can build confidence, deepen their understanding of linear functions, and be better prepared for more advanced mathematical explorations.
What is the easiest way to remember the slope-intercept form?

+
Think of the form as “y equals m times x plus b” where “m” is the rise over run and “b” is where the line hits the y-axis. The phrase can help you remember that slope (m) comes first, followed by the y-intercept (b).
How do you graph a line using the slope-intercept form?

+
Start by plotting the y-intercept on the y-axis. From there, use the slope to determine how many units you rise or fall over how many units you run horizontally to plot additional points on the line.
What are common mistakes when working with slope intercept form?

+
Frequent errors include forgetting to convert an equation to the correct form, misunderstanding how to read negative slopes or y-intercepts, and miscalculating slopes or intercepts from given points.
Can you find the slope-intercept form from just one point and the slope?

+
Yes, if you know the slope (m) and have one point on the line (x₁, y₁), you can find the equation by substituting these values into the form y = mx + b, then solve for b.
How does slope-intercept form help in real-life applications?
+It allows us to model linear relationships like predicting financial growth, determining costs based on usage, understanding speed and distance, or interpreting physical phenomena like acceleration and velocity.