5 Tips for Writing Linear Function Equations Easily
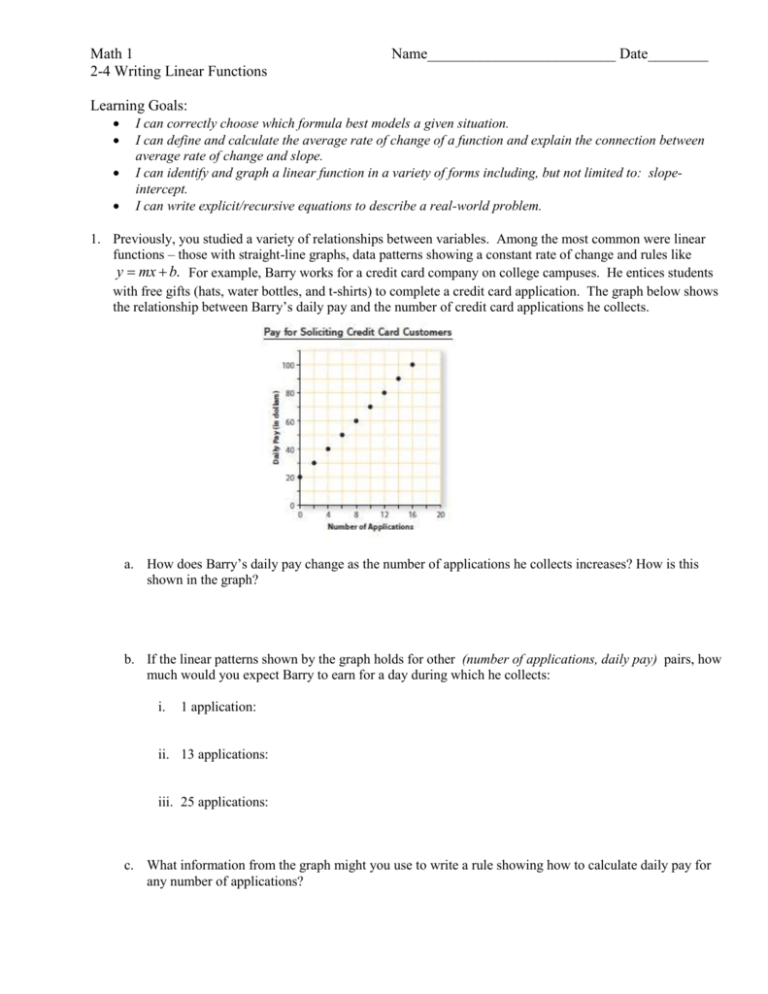
Linear function equations are a cornerstone in algebra, providing the foundation for more advanced mathematical concepts and applications in various fields such as economics, physics, and computer science. Whether you are a student looking to master these equations or someone who uses them in everyday work, understanding how to write linear function equations with ease can significantly streamline your mathematical tasks. Here, we outline five tips that will make writing linear function equations not just simpler but also more intuitive.
Understand the Basics of Linear Functions

Before diving into the tips, it’s crucial to grasp what a linear function is. A linear function has the standard form of y = mx + b, where:
- m represents the slope, indicating the rate of change or steepness of the line.
- b is the y-intercept, the point where the line crosses the y-axis.
1. Visualize the Slope

One of the simplest ways to understand and write a linear equation is by visualizing the slope. Here’s how you can do it:
- Rise Over Run: The slope (m) is often described as “rise over run,” which means how much the line rises or falls as it moves horizontally. For example, if the line rises 2 units for every 3 units moved to the right, the slope would be 2⁄3.
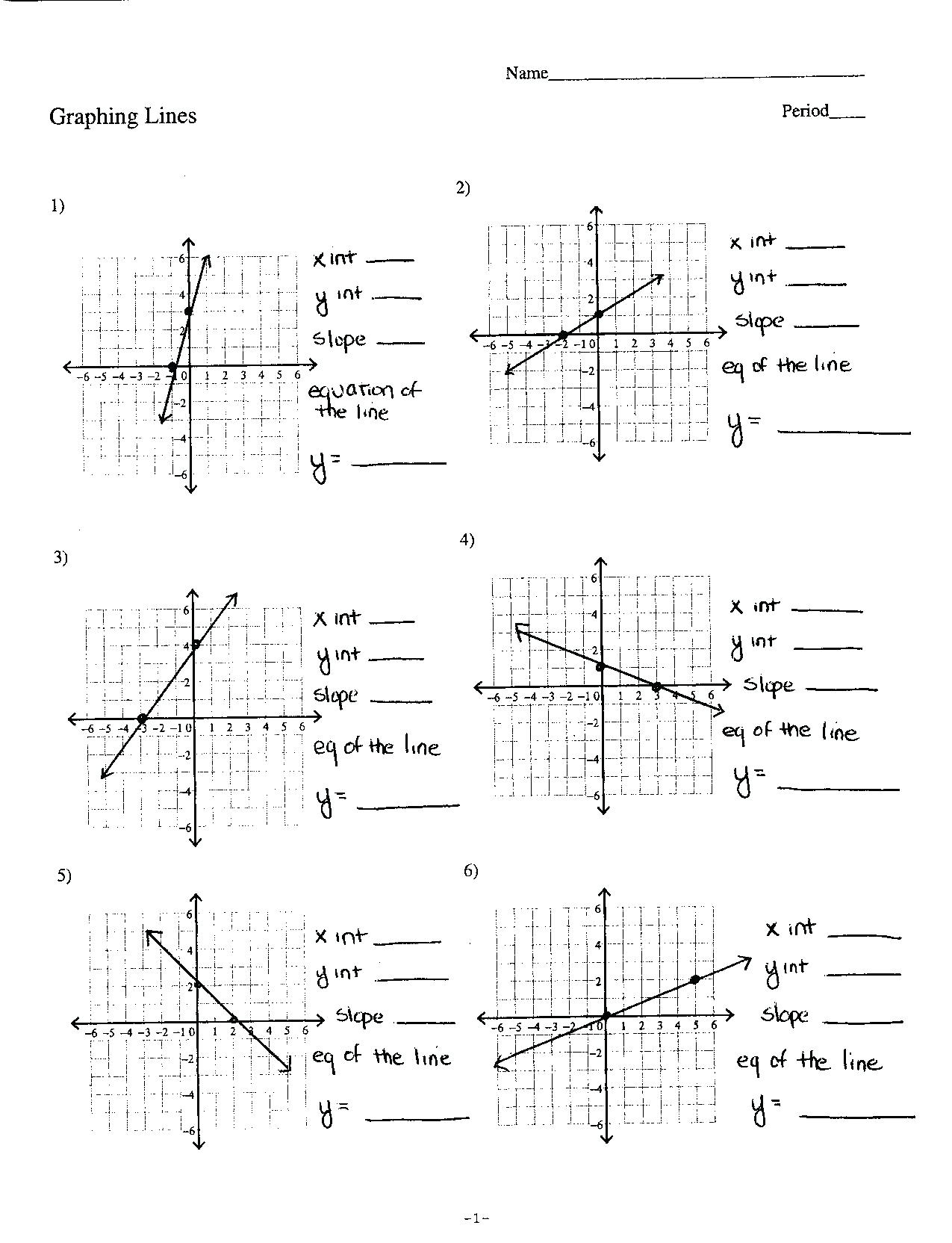
- Using Graph: Plot known points on a graph and connect them with a straight line. Observe the slope and count the units to determine m.

2. Know Your Y-Intercept
The y-intercept is where the line crosses the y-axis. Here are tips for identifying or finding the y-intercept:
- Identify from the Graph: Simply look at the point where the line touches or crosses the y-axis. This point’s coordinate on the y-axis is your y-intercept (b).
- Given Equation: If you have the equation in the form of y = mx + b, the b value directly tells you the y-intercept.
3. Use the Point-Slope Form

When given a point on the line and the slope, you can easily write the equation using the point-slope form, y - y1 = m(x - x1):
- Where (x1, y1) is a point on the line, and m is the slope.
- Example: For a line with a slope of 4 and passing through the point (1, 2), the equation would be y - 2 = 4(x - 1).
📝 Note: Always ensure your line is straight when drawing or estimating points to ensure the slope calculation is correct.
4. Transform to Standard Form

When you need to standardize the equation for comparison or to follow specific conventions, convert any form of linear equation to the standard form Ax + By = C. Here are the steps:
- Start with y = mx + b.
- Move x terms to the left side: A = -m
- Keep the y term on the left side: B = 1
- The y-intercept becomes part of C: C = b
5. Check for Parallel and Perpendicular Lines

Understanding the relationship between lines can help in writing equations:
- Parallel Lines: Have the same slope (m).
- Perpendicular Lines: Their slopes are negative reciprocals of each other. If one line has a slope of m, the other has a slope of -1/m.
By applying these tips, you can write linear function equations with more confidence and accuracy. Remember, practice is key. Here are some important points to keep in mind as you work through problems:
💡 Note: While these tips are geared towards simplifying the process, real-world problems might require understanding additional nuances like equation systems or variable manipulation.
In closing, mastering linear equations involves not just knowing the formula but also understanding the geometric representation and relationships between lines. With these tips, you're better equipped to tackle linear functions in your math or real-world problems. The ability to write these equations accurately and efficiently opens up avenues in analysis, problem-solving, and even basic programming and economic models.
What does the slope tell us about a line?

+
The slope of a line (m in y = mx + b) indicates how steep the line is, or how much y changes for every unit increase in x. It’s the measure of the rate of change.
How do I convert an equation to standard form?
+
To convert y = mx + b to Ax + By = C, move all x terms to the left, keep the y term on the left, and ensure A is positive by multiplying by -1 if necessary.
What if the line has no y-intercept?

+
A vertical line, described by x = a constant, has no y-intercept because it never crosses the y-axis. In the context of the standard form, this becomes a special case where A = 1, B = 0, and C = a constant.