5 Steps to Master Expanded Form of Decimals

Understanding the Basics of Decimals

Before diving into the world of expanded form of decimals, it’s essential to understand what decimals are and how they work. Decimals are a part of the numeral system where a dot or period separates the whole number part from the fractional part. They extend the concept of place value to include fractions and are crucial for precise measurements, financial calculations, and scientific computations.

Step 1: Grasping Place Value in Decimals

The foundation of understanding expanded form in decimals is knowing the place value system. Each digit in a decimal number has a specific place value:
- The digits to the left of the decimal point represent whole numbers, with the place value doubling by a factor of 10 moving to the left.
- Once you reach the decimal point, the place value becomes fractional, and each place to the right of the point reduces by a factor of 10:
| Place Value | Name | Decimal Example |
|---|---|---|
| 100 | Hundreds | 234.56 |
| 10 | Tens | 234.56 |
| 1 | Units (Ones) | 234.56 |
| 0.1 | Tenths | 234.56 |
| 0.01 | Hundredths | 234.56 |
| 0.001 | Thousandths | 234.567 |

Understanding place value is critical for converting a decimal into its expanded form.
Step 2: Identifying Each Digit’s Place Value

To expand a decimal, you need to dissect the number into its individual digits and assign each digit its respective place value. Let’s consider the number 234.56 as an example:
- 2 is in the hundreds place, worth 200.
- 3 is in the tens place, worth 30.
- 4 is in the units place, worth 4.
- 5 is in the tenths place, worth 0.5.
- 6 is in the hundredths place, worth 0.06.
This is the essence of expanding a decimal.

Step 3: Writing in Expanded Form
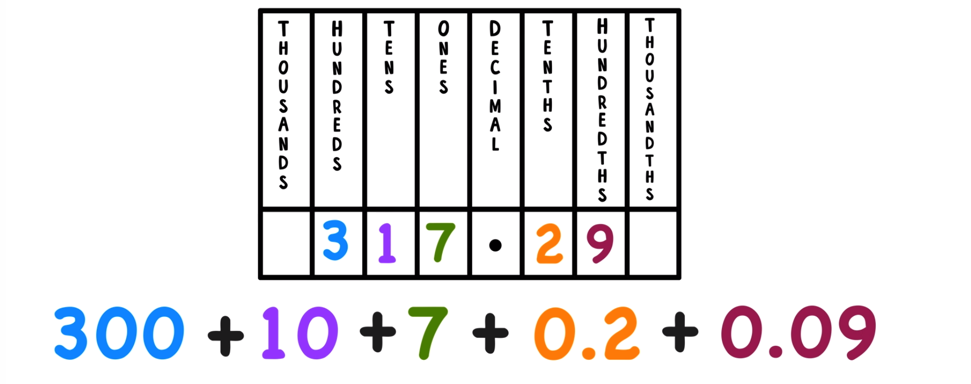
Once each digit’s place value is identified, you can write the number in expanded form:
234.56 in expanded form is 200 + 30 + 4 + 0.5 + 0.06
🔔 Note: When adding each place value, keep the decimal points in place to ensure accuracy.
Step 4: Practice and Application

Mastery comes with practice. Here are a few examples to help solidify your understanding:
- 4.21 becomes 4 + 0.2 + 0.01
- 0.384 becomes 0 + 0.3 + 0.08 + 0.004
- 15.029 becomes 10 + 5 + 0.02 + 0.009
Practicing converting between standard and expanded forms helps reinforce the place value concepts and decimal structure.
Step 5: Understanding Variations in Expanded Form

Expanded form can be written in different ways:
- Using the sum of place values: 234.56 = 200 + 30 + 4 + 0.5 + 0.06
- Using multiplication: 234.56 = (2 × 100) + (3 × 10) + (4 × 1) + (5 × 0.1) + (6 × 0.01)
Each method provides different insights into the nature of decimals and can be useful in various educational or practical settings.
💡 Note: Each representation has its advantages; multiplication is useful for students learning multiplication tables, while addition emphasizes place value directly.
By following these steps, you'll develop a firm understanding of how decimals work and how to express them in expanded form. This proficiency not only helps in academic scenarios but also aids in real-world applications where precision in decimal calculations is critical. Remembering these steps and practicing them regularly can master your skills with the expanded form of decimals.
Why is it important to learn expanded form of decimals?

+
Understanding expanded form helps in breaking down complex numbers into simpler parts, making calculations and conceptual learning easier.
Can the expanded form of decimals be used in real-life scenarios?

+
Absolutely. For instance, when dealing with money, understanding the place value can help you add or subtract amounts accurately, which is essential for budgeting and financial planning.
How can I make learning expanded form more engaging for children?

+
You can use visual aids like base ten blocks, games, or interactive software to make the learning process engaging and visual, helping children understand place value more intuitively.



