5 Easy Steps to Master Mixed Numbers and Improper Fractions

In the world of mathematics, fractions play a crucial role in understanding the division of parts into wholes. Among these, mixed numbers and improper fractions are unique because they offer different representations of the same value but are often misunderstood. Whether you're a student, a parent helping with homework, or someone returning to math after a long hiatus, mastering these concepts can significantly enhance your numerical literacy. Here are five easy steps to master mixed numbers and improper fractions:
Step 1: Understand the Basics

Before diving into the transformation process, let’s solidify the basics:
- Mixed Number: A mixed number combines a whole number and a proper fraction. For example, 2 1/4 means 2 wholes plus a part equal to 1 out of 4.
- Improper Fraction: This type of fraction has a numerator greater than or equal to its denominator. An example is 9/4.
📝 Note: Remember, mixed numbers always appear as Whole Number Fraction while improper fractions show the Numerator/Denominator format.
Step 2: Convert Mixed Numbers to Improper Fractions

Converting a mixed number into an improper fraction involves the following steps:
- Multiply the whole number by the denominator of the fraction.
- Add this result to the numerator of the fraction.
- The denominator remains unchanged.
For example, let’s convert 2 1/4 into an improper fraction:
- 2 (whole number) × 4 (denominator) = 8
- 8 + 1 (numerator) = 9
- So, 2 1/4 becomes 9/4.
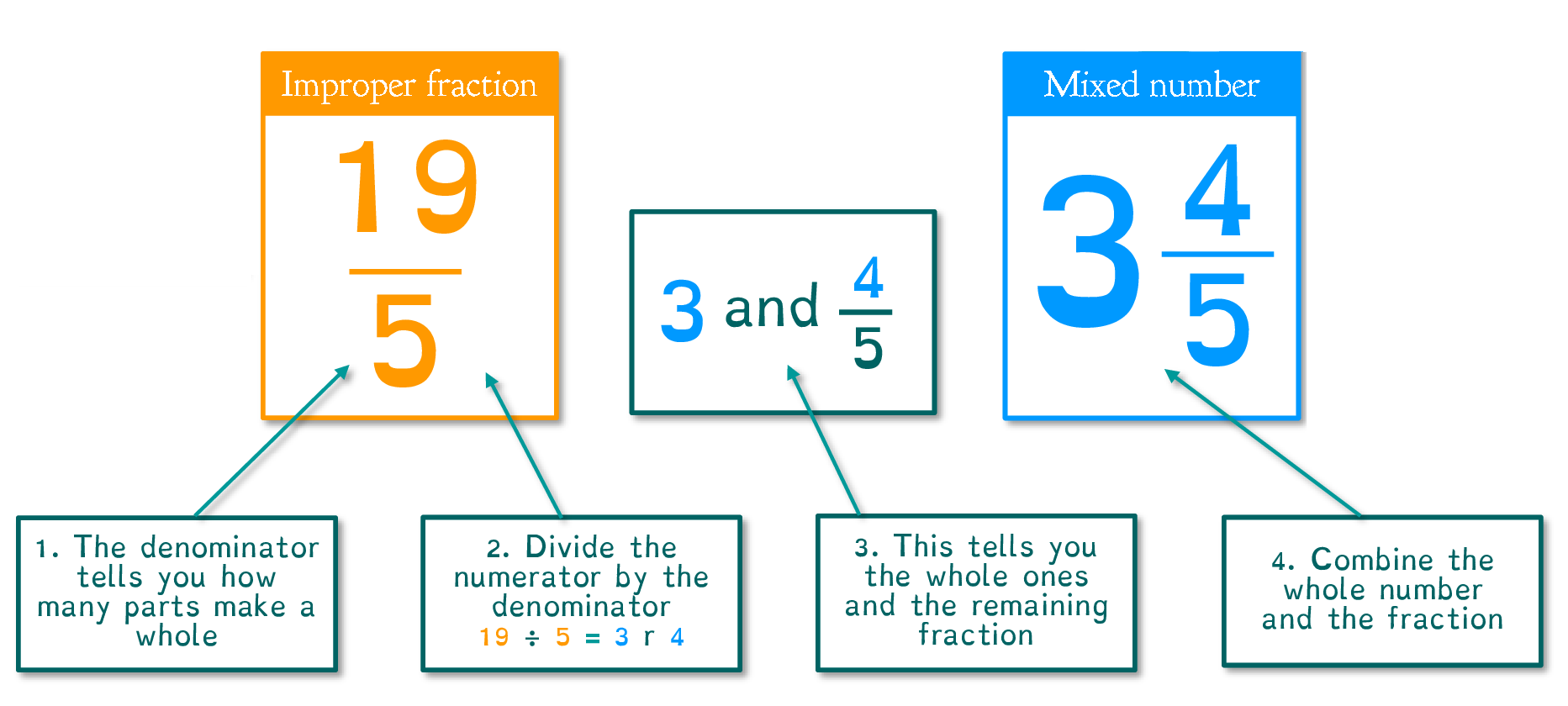
Step 3: Convert Improper Fractions to Mixed Numbers

The reverse process involves these steps:
- Divide the numerator by the denominator to find the whole number part.
- Use the remainder for the numerator of the remaining fraction, keeping the original denominator.
Here’s how we convert 9/4 back into a mixed number:
- 9 ÷ 4 = 2 with a remainder of 1
- Thus, 9/4 equals 2 1/4.
Step 4: Comparing and Ordering

One common need in mathematics is to compare or order mixed numbers and improper fractions. Here are some tips:
- To compare, convert all to the same form (usually improper fractions) for simplicity.
- If mixed numbers, compare the whole numbers first; if they’re equal, compare the fractions.
- To order, arrange the fractions or mixed numbers in ascending or descending order based on their value.
To illustrate, let’s compare 2 1/4 and 2 2/3:
- Convert to improper fractions: 2 1/4 = 9/4 and 2 2/3 = 8/3
- Find a common denominator (12): 9/4 = 27/12 and 8/3 = 32/12
- 27/12 < 32/12, so 2 1/4 < 2 2/3
| Fraction Type | Original Form | Converted Form |
|---|---|---|
| Mixed Number | 2 1/4 | 9/4 |
| Improper Fraction | 9/4 | 2 1/4 |
| Mixed Number | 2 2/3 | 8/3 |

Step 5: Real-Life Application

To cement your understanding of these concepts, try applying them in everyday scenarios:
- Cooking: Adjust recipes when serving more or fewer people.
- DIY Projects: Measure and cut materials with precision.
- Finance: Understanding proportions in investments or dividing profits.
Here’s a brief example with cooking:
Imagine a recipe calls for 2 1/2 cups of flour. If you need to make half the recipe, you’ll use 5/2 cups divided by 2:
- Convert 2 1/2 to an improper fraction: 5/2
- Half of 5/2 is 5/2 × 1/2 = 5/4
- Convert back to mixed number: 5/4 = 1 1/4
💡 Note: Real-life applications make math more engaging and relatable, increasing retention and understanding.
Understanding mixed numbers and improper fractions not only enhances your proficiency in basic arithmetic but also sharpens your problem-solving skills in various contexts. From these five steps, you've learned the essentials of converting, comparing, and applying these concepts in real life. Now, you can confidently navigate through mixed numbers and improper fractions, bringing clarity to this foundational element of mathematics.
What is the difference between a mixed number and an improper fraction?

+
A mixed number combines a whole number and a fraction, where the fraction’s numerator is less than its denominator. For example, 2 1/4. An improper fraction has a numerator greater than or equal to its denominator, like 9/4.
Why do we need to convert mixed numbers to improper fractions?
+
Converting mixed numbers to improper fractions simplifies mathematical operations such as addition, subtraction, multiplication, and division. It also makes it easier to compare and order fractions.
How can I quickly check if a fraction is proper or improper?

+
If the numerator is less than the denominator, the fraction is proper. If the numerator is equal to or greater than the denominator, it’s improper. A mixed number is always a combination of a whole number and a proper fraction.