5 Essential Tips for Calculating Prism Surface Area
The art of calculating the surface area of a prism is fundamental for students, architects, engineers, and anyone interested in 3D modeling. A prism, by definition, has two congruent polygonal bases and rectangular lateral faces. This seemingly simple shape can have infinite forms depending on the base, but the calculation of its surface area remains straightforward with the right approach. Here are five essential tips to help you master the calculation of a prism's surface area.
Understanding Prism Basics

Before diving into calculations, it’s crucial to understand what constitutes a prism:
- Bases: These are identical polygons, typically placed parallel to each other.
- Lateral Faces: These are rectangles or parallelograms connecting corresponding sides of the bases.
💡 Note: Prism sides can be any polygon, not just triangles or squares.
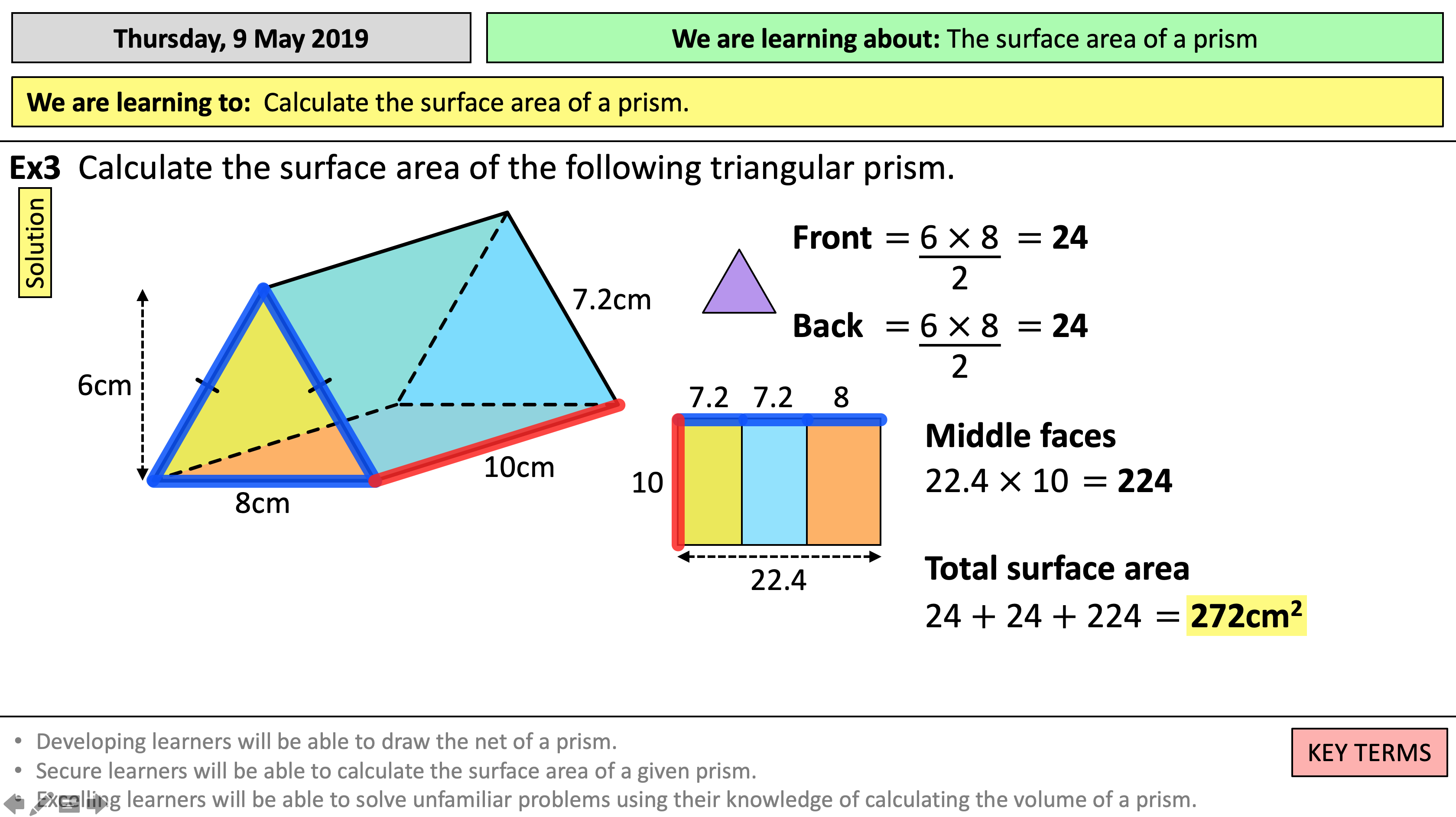
Identify the Base Area

The first step in calculating a prism’s surface area is to determine the area of one of its bases. Here’s how:
- Area of Base: If the base is a triangle, use the formula (base x height) / 2. For a rectangle, it’s length x width. More complex polygons can be subdivided into simpler shapes for easier calculation.
Calculate Lateral Area

The lateral area of a prism is the sum of the areas of all its lateral faces:
- Perimeter: Find the perimeter of the base. For a triangle base, this would be the sum of all sides.
- Height of Prism: Measure or derive the height of the prism. This height is the perpendicular distance between the two bases.
- Formula: Lateral Area = Perimeter of Base x Height of Prism.
📌 Note: Ensure that the height measurement is consistent with the base perimeter for accurate calculation.
Add Lateral and Base Areas

To find the total surface area, sum the lateral area and twice the base area since prisms have two bases:
- Total Surface Area = Lateral Area + (2 x Area of Base)
Account for Complex Shapes

Prism bases can be complex polygons or even irregular shapes:
- Breakdown: Subdivide the base into simpler geometric shapes if necessary to calculate the area. Use trigonometry or known area formulas for each segment.
- Approximation: Sometimes, exact areas can be complex; approximations might be needed.
In summary, mastering the calculation of a prism's surface area involves understanding its basic structure, accurately identifying the area of the base, calculating the lateral area, and summing these values. Whether dealing with simple prisms like cubes or more complex shapes, the principles remain the same, with slight adaptations for each unique base shape.
To wrap up, always ensure your measurements are accurate, double-check your calculations, and remember that a solid understanding of geometry will make these calculations second nature.
Why is understanding prisms important?

+
Understanding prisms is crucial in fields like architecture, where building volumes are calculated, engineering for design and analysis, and even in everyday applications like packaging and logistics.
Can I use the same formulas for calculating surface area for all prisms?

+
Yes, the basic formulas hold true for all prisms, but the approach to finding the area of the base might vary depending on its complexity.
How can I verify if my surface area calculation is correct?

+
After calculating, you can compare your results with an online calculator or software like GeoGebra, or manually recheck your calculations with different methods.