5 Tips to Simplify Rational Expressions Easily

Are you stuck in a math problem involving rational expressions? Simplifying them can seem daunting, but with a few strategic tips, you can master the process. Here are five practical tips to simplify rational expressions quickly and efficiently.
Finding Common Factors

The first step in simplifying any rational expression is to identify common factors between the numerator and the denominator. Here’s how:
- List all the factors of both the numerator and the denominator.
- Identify any common factors. These can be numbers or variables.
- Cancel these common factors out.
🔎 Note: Always check if the common factors are not zero since a denominator of zero would make the expression undefined.
Using the Fundamental Theorem of Algebra

The Fundamental Theorem of Algebra tells us that any non-constant polynomial has at least one complex root. This theorem can be particularly useful in simplifying rational expressions:
- Factorize the numerator and denominator completely.
- Apply the theorem to identify and cancel any common factors.
- Simplify by canceling out the matching terms.
Combining Like Terms
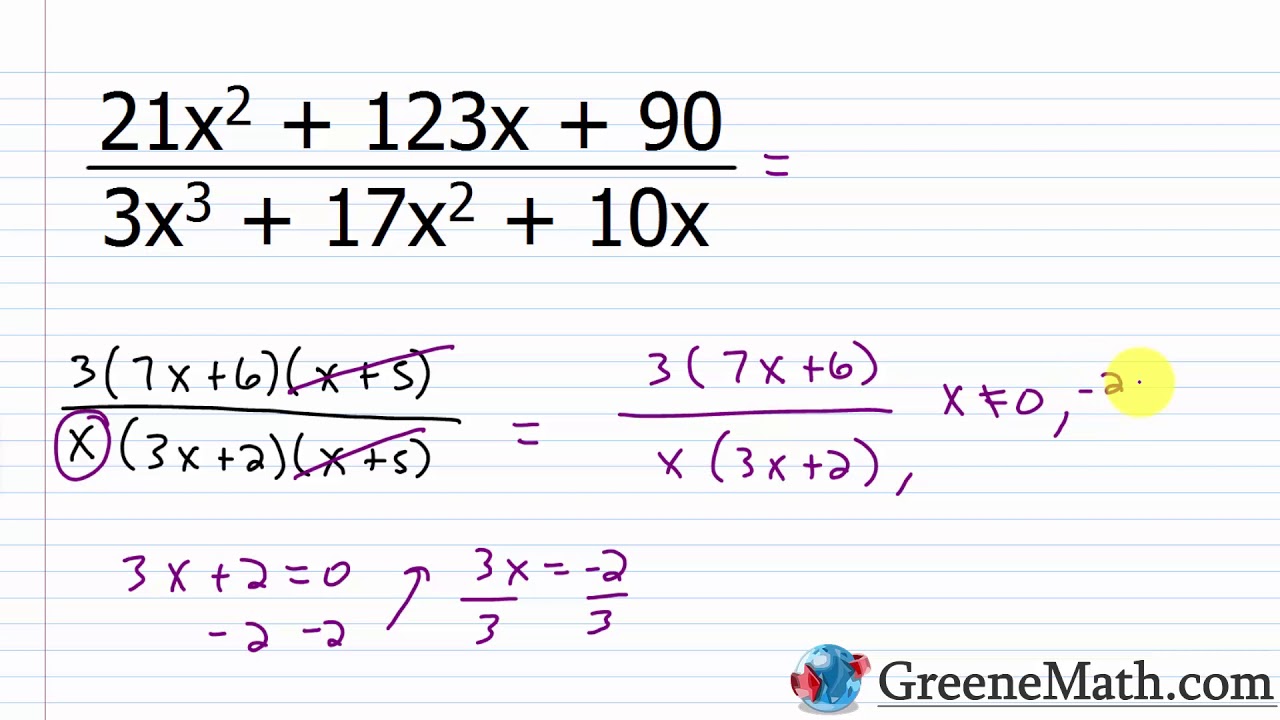
When dealing with rational expressions, combining like terms can make simplification easier:
- Identify terms with the same exponents or constant terms in both numerator and denominator.
- Combine these terms to reduce the expression.
| Expression | Like Terms | Reduced |
|---|---|---|
| (x2 + 5x + 6)/(x2 + 2x + 3) | x2 | (5x + 6)/(2x + 3) |

Dividing by the Greatest Common Divisor (GCD)

To simplify efficiently, you can:
- Find the GCD of both the numerator and the denominator.
- Divide both by this GCD, simplifying the expression.
🔎 Note: The GCD approach is especially effective for expressions with large or complex polynomials.
Expanding and Cross Cancelling

Sometimes expanding the terms can lead to a simpler cancellation:
- Expand any factored terms in the numerator or denominator.
- Look for common factors that can be cross-cancelled.
This technique can help reduce the complexity of the expression before further simplification.
By following these tips, you'll find that simplifying rational expressions becomes a more manageable and less intimidating task. Whether you're working through algebra homework, preparing for an exam, or tackling real-world problems, understanding how to simplify these expressions is invaluable.
Mastering these strategies not only speeds up your ability to solve problems but also deepens your understanding of algebra. So, next time you're faced with a rational expression, remember these steps to streamline the process and make the most out of your mathematical toolkit.
Why is it important to simplify rational expressions?

+
Simplifying rational expressions helps in understanding the behavior of the function, solving equations, and performing arithmetic operations with fewer steps.
What is the difference between factoring and canceling?

+
Factoring involves breaking down an expression into simpler parts or factors. Canceling refers to removing the same factor from both the numerator and the denominator to simplify the expression.
Can all rational expressions be simplified?

+
Not all rational expressions can be simplified, especially if there are no common factors between the numerator and the denominator.



