5th Grade Math: 10 Order of Operations Worksheets Without Exponents

Understanding the order of operations is a foundational skill in mathematics that students must master early in their academic journey. Typically introduced in 5th grade, this concept is not only crucial for solving more complex math problems later but also enhances logical thinking and problem-solving capabilities. In this blog post, we'll explore the Order of Operations, commonly known as PEMDAS or BODMAS, and provide you with 10 carefully crafted worksheets tailored for 5th graders that don't include exponents. These worksheets will help reinforce the concept and ensure students are well-prepared for algebraic concepts in future classes.
What is the Order of Operations?

The order of operations is a set of rules used to unambiguously define how mathematical expressions are evaluated. Here’s a breakdown:
- Parentheses: Operations enclosed in parentheses or brackets are done first.
- Exponents or Order (squares, cubes, etc.): Though we’ll avoid exponents in our worksheets, this rule typically follows parentheses.
- Multiplication and Division: Next, perform multiplication and division from left to right.
- Addition and Subtraction: Lastly, perform addition and subtraction from left to right.

Worksheet 1: Basic Order of Operations

This worksheet introduces students to the basic principles of the order of operations without the complexity of exponents. Here are some examples:
| Problem | Work |
|---|---|
| 6 + 4 x 2 | 6 + (4 x 2) = 6 + 8 = 14 |
| (8 - 3) x 3 | (8 - 3) x 3 = 5 x 3 = 15 |

📚 Note: Encourage students to write down the steps for each problem. It helps in understanding the process and in self-checking their work.
Worksheet 2: Mixing Parentheses and Operations

This worksheet aims to solidify the understanding of parentheses as the first step in order of operations.
- Calculate expressions like: (5 + 3) - 2 x 4
- Encourage solving each part in parentheses before moving to multiplication or division.
Worksheet 3: Multi-Step Problems
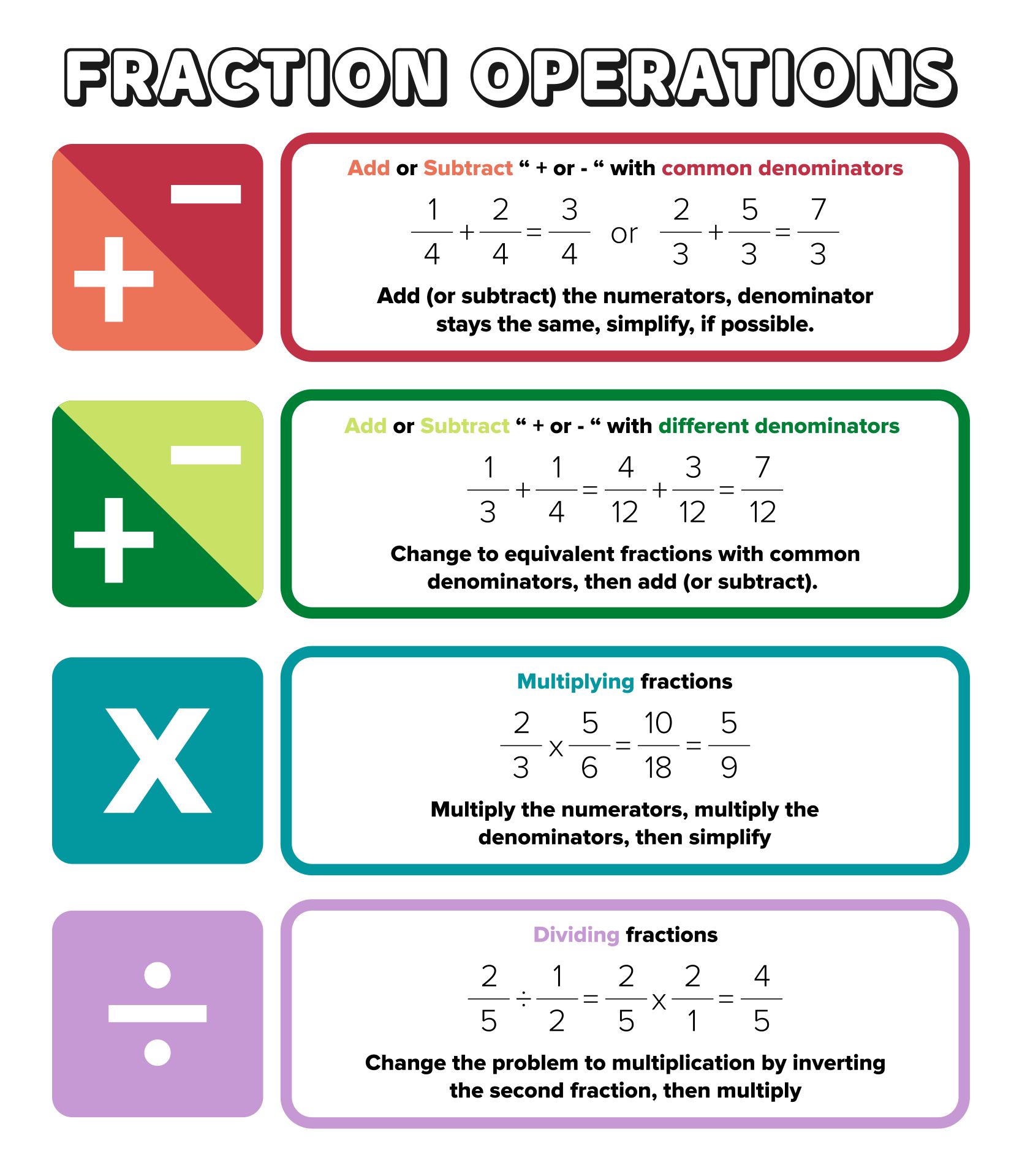
Here, we increase the complexity by including problems with multiple operations. The focus is on correctly applying each step of the order of operations.
- 3 + 2 x 5 - 7
- 8 - (2 + 1) x 3
Worksheet 4: Real-Life Applications

Applying the order of operations in real-life scenarios makes the learning process more engaging.
- Calculate how much money you would have if you bought a 5 toy and received 15 as a gift.
- Determine how many pencils you can buy if each pack contains 8 pencils and costs 2, and you have 20 to spend.
Worksheet 5: Error Analysis

This worksheet requires students to identify and correct mistakes in order of operations problems.
| Problem | Student’s Solution | Correct Solution |
|---|---|---|
| 12 - 4 + 6 | 12 - 10 = 2 | 12 - 4 + 6 = 14 |
Worksheet 6: Word Problems

In this worksheet, students solve mathematical word problems requiring the use of the order of operations:
- Sarah needs to buy 3 packs of stickers for her collection. Each pack costs 4, and she has a 5 bill from her piggy bank. How much change will she get back?
- Calculate the cost of 2 books priced at 15 each and a notebook priced at 3.
Worksheet 7: Chain of Operations

This worksheet focuses on problems where operations are chained together, ensuring students follow the order of operations correctly:
- 20 - 3 x 4 + 2
- 8 + 5 x 6 - 2
Worksheet 8: Misconceptions and Challenges

Here, students tackle problems that commonly cause confusion or mistakes:
- 2 + 3 x 5 - 4
- 8 - 2 x (7 - 4)
Worksheet 9: Time Pressure Test

A timed worksheet to practice quick mental math using the order of operations:
- 10 + 2 x 3 - 1
- 7 x (4 - 2) + 1
🕒 Note: For this worksheet, give students a set time to solve each problem to encourage quick thinking and accuracy under pressure.
Worksheet 10: Fun and Games
This worksheet incorporates fun activities like puzzles or a math scavenger hunt that rely on order of operations:
- Solve math puzzles where the solution to one step is used in the next, requiring careful application of the order of operations.
- A mini treasure hunt where steps involve solving order of operations problems to find the next clue.
As we conclude our journey through these worksheets, remember that mastering the order of operations is more than just following rules; it's about developing a logical approach to problem-solving. Students who understand and apply these rules will be better equipped to handle algebra and beyond. Through consistent practice with these worksheets, 5th graders will not only become proficient in the order of operations but also gain confidence in their mathematical abilities. The variety in these exercises ensures that learning is not monotonous, and the step-by-step nature encourages a thorough understanding, setting a strong foundation for future mathematical concepts.
Why is the order of operations important?

+
The order of operations ensures that mathematical expressions are evaluated consistently, producing the same result regardless of who solves the problem.
Can you simplify PEMDAS?

+
PEMDAS stands for Parentheses, Exponents, Multiplication and Division (from left to right), and Addition and Subtraction (from left to right). It’s a simple mnemonic to remember the order of operations.
What if a problem doesn’t include all parts of PEMDAS?

+
Even if some parts of PEMDAS are missing, you still follow the rules in the order they appear. For instance, if there are no parentheses or exponents, you start with multiplication/division from left to right.
How do I know if I’ve done the order of operations correctly?

+
One way to check is by using the worksheets provided above. If your answers match the solutions, or if you can solve similar problems consistently, you’re likely applying the rules correctly.
Are there any tips for teaching order of operations?

+
Use visual aids, mnemonics like “Please Excuse My Dear Aunt Sally,” and real-life scenarios. Encourage students to explain their process, which helps solidify their understanding.



