5 Easy Steps to Solve Trig Equations: Worksheet Answer Key

If you're grappling with trigonometric equations, don't worry. Solving these equations can become manageable and even enjoyable with the right approach. This article provides a detailed worksheet answer key on trigonometric equation solving, breaking it down into five straightforward steps. By following these steps, you'll gain confidence in your trigonometry skills, and your problem-solving abilities will sharpen significantly.
Understanding Trigonometric Equations


Trigonometry often evokes a mix of emotions—curiosity, frustration, and sometimes awe, due to its integral role in understanding periodic functions and their applications. Here are the basic types of trigonometric equations you might encounter:
- Linear Equations: Involving one trigonometric function, such as
sin(x) = 1/2 - Quadratic Equations: Including expressions like
cos²(x) + sin(x) = 0 - Periodic Equations: Dealing with multiple angles, e.g.,
tan(2x) = √3
Step 1: Isolate the Trigonometric Function


Isolation of the trigonometric function is crucial as it simplifies the equation:
- Remove all coefficients from the trigonometric term.
- Move all terms involving trigonometric functions to one side of the equation.
| Original Equation | Isolated Equation |
|---|---|
| 2sin(x) + 1 = 0 | sin(x) = -1/2 |

📝 Note: Ensure the isolated term is a single trigonometric function or a simple expression.
Step 2: Determine the Interval

Trigonometric functions have periodicity, which means you’ll need to identify a specific interval within which you are solving the equation:
- For sine, cosine, secant, and cosecant, the standard interval is [0, 2π].
- For tangent and cotangent, the interval is [0, π).
📌 Note: Understand the periodicity to find all possible solutions beyond this interval.
Step 3: Solve for x


Now, solve for x within the determined interval. Here are the methods:
- Use unit circle values for basic trigonometric values.
- Apply inverse trigonometric functions like
arcsin, arccos, arctan. - Solve by equating the given trigonometric expression to known angles within the interval.
💡 Note: Remember that the inverse functions yield multiple solutions due to periodicity; ensure you capture all in your solution set.
Step 4: Find General Solutions

Trigonometric equations typically have solutions that repeat over time. Here’s how to find general solutions:
- Let the specific angle be
θ. For sine and cosine, use:x = θ + 2kπx = π - θ + 2kπ
- For tangent, use:
x = θ + kπ
✨ Note: Here, k is any integer representing the periodicity of the function.
Step 5: Verify the Solutions


It’s always good practice to verify your solutions to ensure accuracy:
- Plug back into the original equation and simplify to confirm if it's still true.
- Consider boundary cases if solving within a restricted interval.
By following these five steps systematically, you'll transform trigonometric equation solving from a complex task into a manageable process. The knowledge and confidence you'll gain from mastering these techniques will prove invaluable, not only in trigonometry but also in various applications across engineering, physics, and data science.
What is a trigonometric equation?

+
A trigonometric equation is an equation involving one or more trigonometric functions of a variable, typically x. Solving such equations often involves using trigonometric identities, periodicity, and inverse functions.
How do I know if I’ve solved a trigonometric equation correctly?

+
To verify solutions, plug the values back into the original equation, simplify, and check if the equation holds true. Also, ensure all solutions within the given interval are captured and verified.
Why are some solutions in a restricted interval?
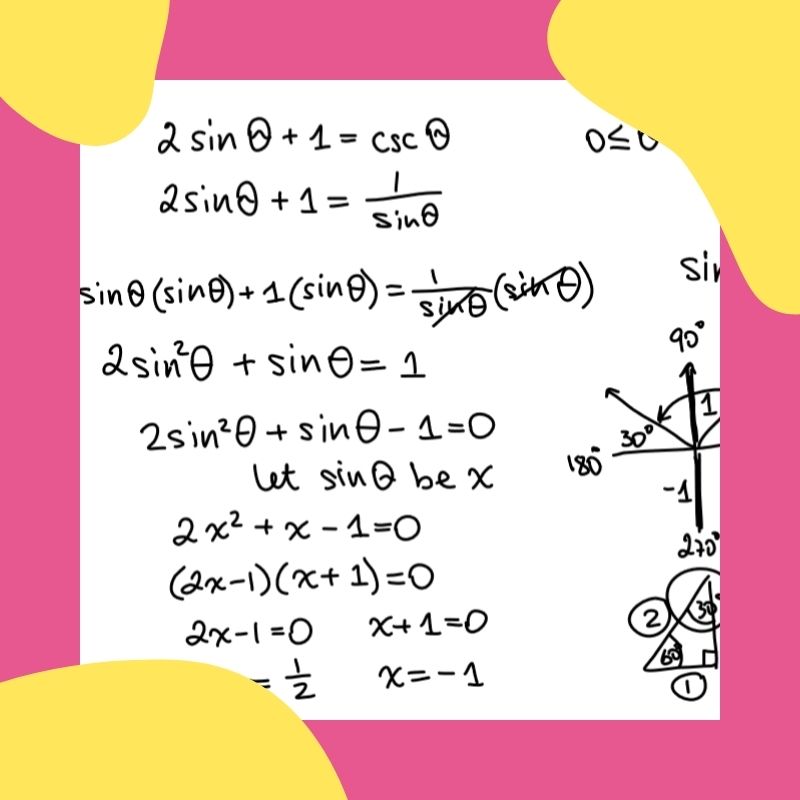
+
Solutions are often provided within a restricted interval because trigonometric functions are periodic. This means solutions repeat at regular intervals. A standard interval is chosen to avoid listing infinite solutions.
What’s the difference between sine and cosine equations?

+
While both sine and cosine equations can be solved using similar steps, their periodicity and solutions differ slightly. Cosine functions have maximums at integer multiples of π, whereas sine functions peak at odd multiples of π/2.
Can trigonometric equations have no solutions?

+
Yes, some trigonometric equations can have no real solutions if the conditions they impose on the trigonometric functions cannot be satisfied for any angle x.