5 Essential Tips for Coordinate Geometry Worksheet Success

When tackling the world of coordinate geometry, students often find themselves at crossroads between algebra and geometry. This branch of mathematics deals with the study of shapes and their properties using coordinates, a skillset that's not only essential for advanced mathematical studies but also for practical applications in fields like engineering, physics, and computer graphics. To ensure success in mastering coordinate geometry worksheets, here are five indispensable tips:
1. Understand the Basics

Begin with a solid foundation in basic concepts. Coordinate geometry revolves around understanding the Cartesian plane, which consists of two number lines intersecting at right angles:
- The x-axis (horizontal).
- The y-axis (vertical).
Key points to grasp include:
- How to plot points using ordered pairs (x, y).
- Understanding the slope of a line, expressed as m = (y₂ - y₁) / (x₂ - x₁).
- The distance formula between two points: d = √[(x₂ - x₁)² + (y₂ - y₁)²].
- The equation of a line in various forms (slope-intercept form, point-slope form, etc.).
🔍 Note: These fundamental concepts are the building blocks for all coordinate geometry problems. Mastery here sets the stage for complex geometric calculations.
2. Practice with Different Types of Problems

Coordinate geometry worksheets often include a variety of problem types:
- Distance and Midpoint Calculations
- Slope and Equation of Lines
- Intersection of Lines
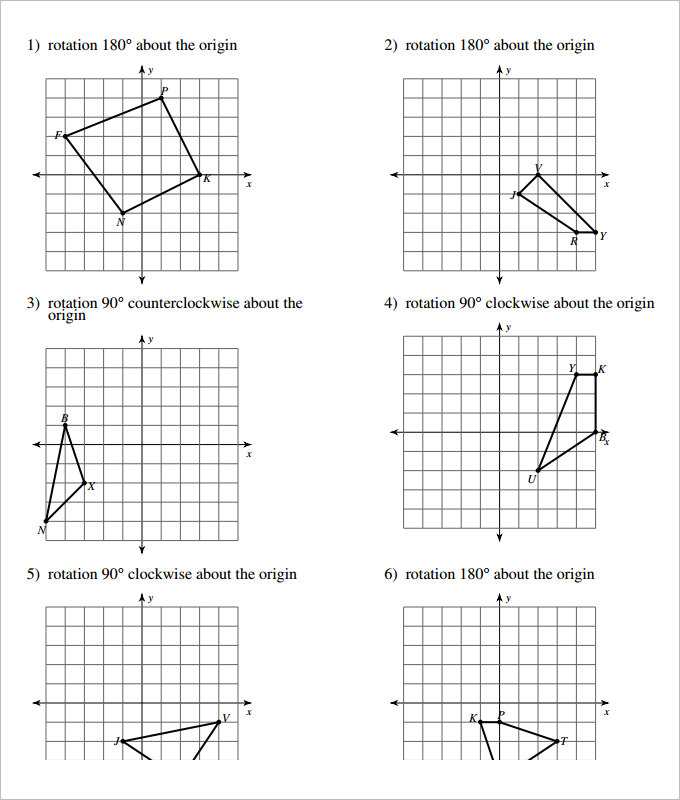
- Reflection, Translation, and Rotation of Points and Shapes
By practicing these different aspects:
- You’ll enhance your ability to recognize which formulas or theorems to apply.
- Your speed and accuracy in solving problems will improve.
Regular exposure to varied problems ensures that you’re not only prepared for typical worksheet questions but also for any unexpected twists.
3. Use Graphing Calculators or Software

Technology can be a powerful ally in coordinate geometry:
- Graphing Calculators: Tools like TI-84 or TI-Nspire provide quick graphing and computational aid for complex equations.
- Software Solutions: Applications like GeoGebra, Desmos, or Autograph allow for dynamic graphing, geometric transformations, and even 3D visualization.
These tools offer a visual understanding of coordinate geometry, which is invaluable for:
- Confirming algebraic calculations.
- Understanding how changes in coordinates affect shape and position.
📚 Note: While technology aids in understanding, ensure you can perform calculations manually for exams where calculators might not be allowed.
4. Sketch and Visualize

Even when using technology, sketching graphs and visualizing the problem:
- Helps you understand the geometric implications of equations.
- Provides a mental model to solve complex problems.
When sketching:
- Mark key points and lines clearly.
- Label important coordinates and intercepts.
- Use different colors or markers to distinguish between lines, points, or segments.
Your sketches don’t need to be perfect; they should be functional and aid in your problem-solving process.
5. Reflect on Your Solutions
After solving problems:
- Review your work. Did you use the right formulas?
- Understand why your solution works. What geometric principles are at play?
- If you made a mistake, learn from it. What can you do differently next time?
Reflection is key to deepening your understanding of coordinate geometry, helping you to:
- Recognize patterns in problems.
- Avoid common errors.
- Develop a more intuitive approach to geometric thinking.
By consistently applying these tips, you’ll navigate through coordinate geometry worksheets with greater ease and accuracy, transforming a once daunting subject into a manageable and even enjoyable part of your mathematical journey.
Why is coordinate geometry important?
+
Coordinate geometry is crucial because it provides a bridge between algebra and geometry, allowing us to analyze geometric figures using algebraic techniques. This intersection is fundamental in various applied sciences, engineering, and technology.
How can I improve my speed in solving coordinate geometry problems?

+
Practice is key, but also:
- Work on mental math for basic calculations.
- Memorize key formulas and theorems.
- Use shortcuts when possible, like recognizing simple geometric properties.
What are some common mistakes in coordinate geometry?

+
Common mistakes include:
- Misapplying distance or midpoint formulas.
- Confusing coordinate signs.
- Forgetting to check for vertical or horizontal lines.
- Overlooking quadrants when dealing with angles.
Related Terms:
- Geometry
- Trigonometry
- Algebra
- Euclidean geometry
- Analytic geometry
- Coordinate geometry worksheet pdf