5 Tips for Calculating Rectangular Prism Volume Easily

📝 Note: Please use a calculator or paper for manual calculations.
Introduction to Rectangular Prism Volume Calculation

Calculating the volume of a rectangular prism might sound like an elementary task, but it becomes indispensable in a variety of applications, from construction to design. The volume of a rectangular prism represents the space it occupies, and it’s essential for determining how much material you need, the capacity of containers, and many other practical tasks. In this post, we’ll explore five straightforward tips that make calculating the volume of a rectangular prism not just simple, but enjoyable and insightful.
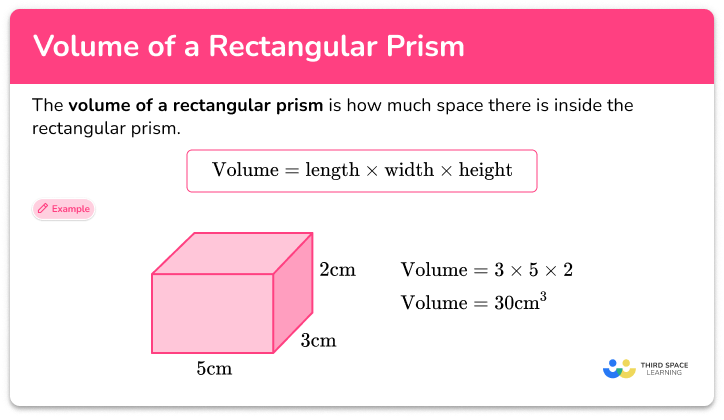
1. Understand the Basic Formula

Let’s start with the foundation of volume calculation:
- Volume (V) = Length (L) x Width (W) x Height (H)
Here are a couple of tips to keep in mind:
- Ensure all measurements are in the same unit (meters, centimeters, inches, etc.) for consistency.
- The order of the multiplication doesn't matter. You can multiply in any order, but it's typically easier to calculate in sequence.
2. Visualize the Prism

To make calculations easier, visualize your rectangular prism. Imagine filling it with water or stacking blocks to fill the shape:
- Think of it as a stack of books or layers of a cake.
- Visualize filling the prism with cubes, and count how many cubes fit in each layer and how many layers there are.
3. Use Dimensional Analysis

Dimensional analysis is a technique that helps keep your units in check:
| Step | Description |
|---|---|
| 1. | Write out your calculation with units included: L cm x W cm x H cm = (L x W x H) cm3. |
| 2. | Check that your final unit of measurement is cubic. |
| 3. | If your initial measurements are in different units, convert them all to a common unit before calculating. |
4. Leverage Online Calculators and Apps

In the digital age, there's no need to do everything manually:
- Many online calculators or apps provide instant volume calculations. They can handle different unit conversions and often come with step-by-step explanations.
- Check for apps specifically designed for volume calculations; some even offer visualization tools.
5. Practice, Practice, Practice

Like any skill, proficiency in calculating volumes comes with practice:
- Try calculating the volume of everyday objects like your desk, laptop, or a box of cereal.
- Set up a collection of simple rectangular items and challenge yourself or others to find their volumes quickly.
📊 Note: Always double-check your calculations to avoid errors, especially in professional settings where accuracy is crucial.
By understanding the fundamental principles, visualizing the process, employing dimensional analysis, using technology, and practicing regularly, calculating the volume of a rectangular prism becomes an effortless task. This knowledge not only simplifies practical problem-solving but also adds a layer of confidence and competence when dealing with measurements in various fields.
Why is it important to have all measurements in the same unit?

+
Having all measurements in the same unit ensures that your calculation is consistent, allowing for accurate volume calculation.
Can the volume be calculated if one of the dimensions is given in feet while the others are in inches?

+
Yes, but you need to convert all dimensions to the same unit (either feet or inches) before you multiply them together.
What if the dimensions provided are not exact?
+
If dimensions are not exact, you should consider the accuracy you need. Often, rounding to the nearest decimal place or whole number will suffice, but in some professional scenarios, precision is key.
📝 Note: When dealing with multiple dimensions, ensure all measurements are accurate to avoid miscalculations. If possible, verify the dimensions using a tape measure or ruler.
In conclusion, calculating the volume of a rectangular prism can be straightforward with these tips. Whether for educational purposes or practical applications, these tips help to make volume calculation an enjoyable and insightful experience. By understanding the formula, visualizing the process, using dimensional analysis, leveraging technology, and practicing regularly, you can gain mastery over this seemingly simple but fundamentally important mathematical operation.
Why is it important to have all measurements in the same unit?
+
Having all measurements in the same unit ensures that your calculation is consistent, allowing for accurate volume calculation.
Can the volume be calculated if one of the dimensions is given in feet while the others are in inches?

+
Yes, but you need to convert all dimensions to the same unit (either feet or inches) before you multiply them together.
What if the dimensions provided are not exact?
+
If dimensions are not exact, you should consider the accuracy you need. Often, rounding to the nearest decimal place or whole number will suffice, but in some professional scenarios, precision is key.
Can volume calculations be used for something other than simple shapes?

+
Yes, the principle of volume calculation can be applied to more complex shapes by breaking them down into simpler forms or using more advanced calculus techniques for irregular shapes.
What are the common mistakes made when calculating volume?

+
Common mistakes include using incorrect units, misreading measurements, incorrect calculation of dimensions (such as length, width, and height), and forgetting to apply dimensional analysis. Always double-check your units and calculations.



