Volume of Shapes Worksheet: Your Ultimate Guide

Welcome to your ultimate guide for understanding and calculating the volume of shapes. Whether you're a student delving into geometry or someone curious about everyday math, this post will equip you with the knowledge to confidently tackle volume calculations for various shapes.
Understanding Volume
Volume represents the amount of space that a 3D shape occupies. Here's how to conceptualize it:
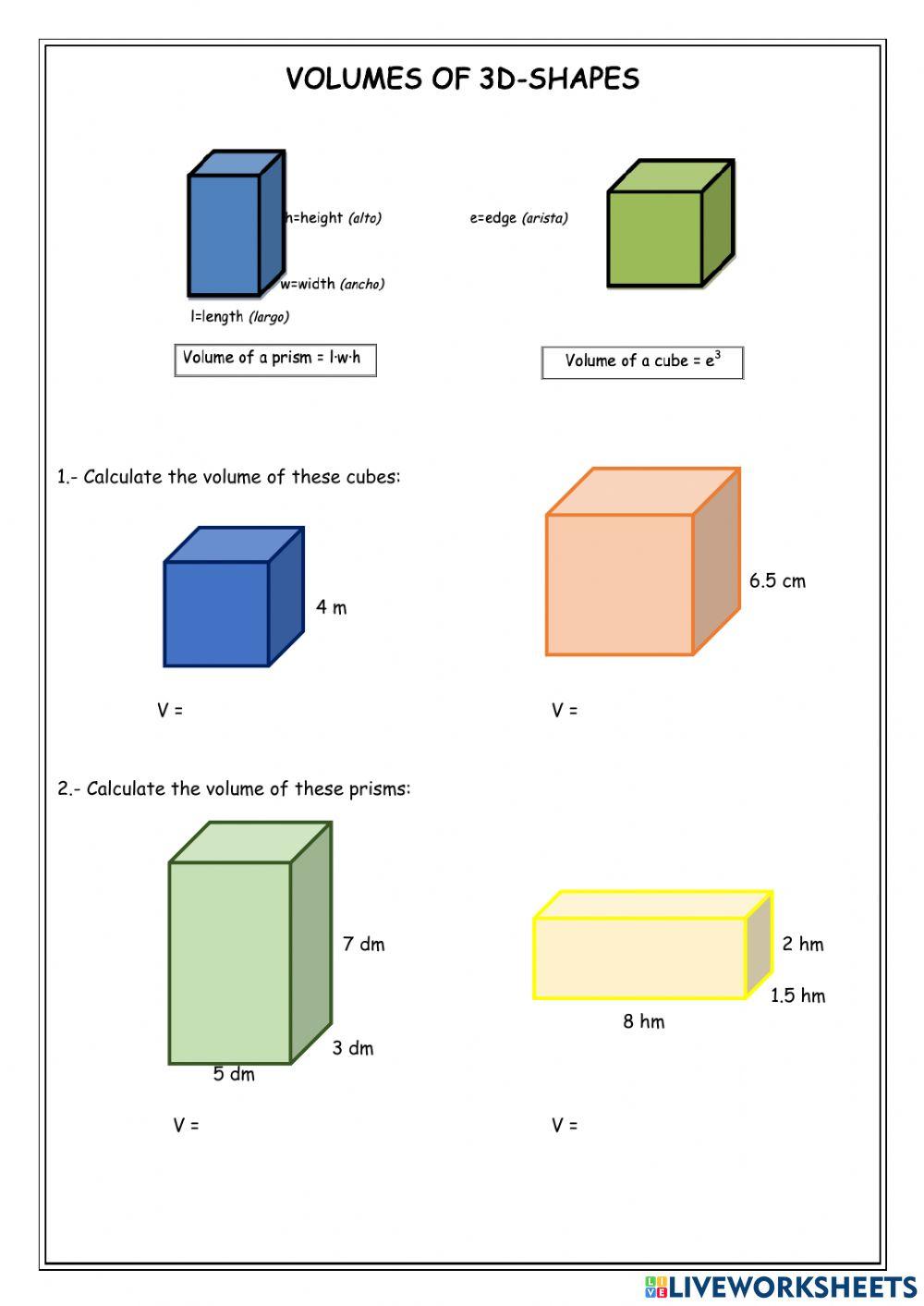
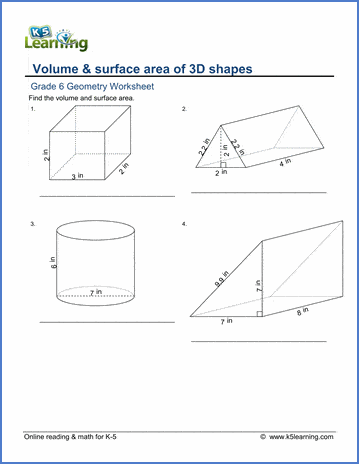
- Cuboid or Rectangular Prism: V = length x width x height
- Cube: V = side3
- Cylinder: V = πr2h
- Cone: V = (1/3)πr2h
- Sphere: V = (4/3)πr3
- Pyramid: V = (1/3)Base Area x height
Volume of Basic Shapes
Let's dive into the formulas and practical examples for basic shapes:
Cuboid or Rectangular Prism
A cuboid’s volume is calculated by multiplying its length, width, and height:
V = l x w x h
Example: If a room measures 6 meters long, 4 meters wide, and 3 meters high, its volume would be:
6 x 4 x 3 = 72 cubic meters
📝 Note: The units must be consistent; if you mix units (e.g., feet and meters), the volume will be incorrect.
Cube

Since all sides of a cube are equal, you simply cube the length of one side:
V = a3
Example: A dice with each side measuring 1.5cm has a volume of:
1.5 x 1.5 x 1.5 = 3.375 cubic cm
Cylinder

Think of a cylinder as a stack of circular pancakes:
V = πr2h
Example: A cylindrical water tank with a radius of 2m and a height of 5m:
V = π(2)2(5) = 20π ≈ 62.83 m3
📐 Note: Ensure you use the radius, not the diameter, when calculating the volume of a cylinder.
Cone
Similar to a cylinder, but with a pointed end:
V = (1⁄3)πr2h
Example: An ice cream cone with a radius of 2 inches and a height of 6 inches:
V = (1⁄3)π(2)2(6) = 8π ≈ 25.13 cubic inches
Sphere
Like a ball, here’s how you find its volume:
V = (4⁄3)πr3
Example: A basketball with a radius of 0.23 meters:
V = (4⁄3)π(0.23)3 ≈ 0.054 m3
⚽ Note: Remember to cube the radius when calculating a sphere's volume.
Pyramid

Whether it’s a square or triangular base:
V = (1⁄3)Base Area x height
Example: A pyramid with a square base of side 5cm and height 10cm:
V = (1⁄3) x (5 x 5) x 10 = 83.33 cubic cm
Advanced Volume Calculations

Beyond basic shapes, here are some more complex volume calculations:
| Shape | Formula | Example |
|---|---|---|
| Ellipsoid | V = (4/3)πabc | Assume a = 3, b = 4, c = 5; V ≈ 251.33 |
| Frustum of a Cone | V = (1/3)πh(R2 + Rr + r2) | R = 3, r = 1, h = 4; V ≈ 50.26 |

These formulas are less common but useful for precise volume calculations:
- Frustum of a Pyramid requires summing up the volumes of smaller pyramids inside it.
- Paraboloid uses a formula involving the base area and height: V = (1/2)πr2h
Tips and Techniques
Here are some tips for mastering volume calculations:
- Unit Consistency: Always check that your units match throughout the calculation.
- Decompose Complex Shapes: For shapes like L-shaped objects, break them into simpler shapes and calculate their volumes separately.
- Use Calculators: Scientific calculators or apps can help with the number crunching.
Practical Applications

Volume calculation isn't just for classrooms; here are some real-life applications:
- Architecture: Designing buildings and structures.
- Cooking: Recipes often require volume measurements.
- Shipping and Packaging: To ensure items fit in boxes.
- Water Displacement: Calculating how much water an object will displace.
🔄 Note: Water displacement volume calculations are based on Archimedes' principle, useful for buoyancy calculations.
Volume calculation is an essential part of understanding and interacting with the world around us. From basic geometric shapes to more complex structures, the principles remain the same, and with practice, these calculations become second nature. Whether you're measuring the space in a room, the amount of material needed for construction, or simply curious about the capacity of your favorite container, the ability to calculate volumes will serve you well in numerous contexts.
What is the difference between volume and surface area?

+
Volume measures the space inside a three-dimensional object, while surface area measures the total area of the object’s surface.
Why is understanding volume important?

+
It’s crucial for applications like construction, manufacturing, engineering, and everyday tasks like cooking or packaging.
Can you calculate the volume of any shape?
+
Generally, yes. However, for irregular shapes, you might need to use calculus or approximation methods like water displacement.



