Cylinder, Cone, Sphere Volume Worksheet Guide
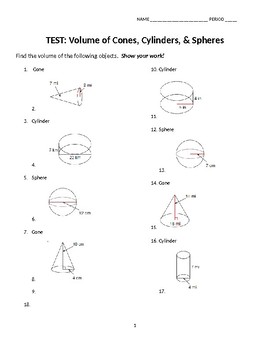
In the exciting world of geometric shapes, understanding the intricacies of volume calculations can significantly deepen your grasp of three-dimensional geometry. This comprehensive guide dives into volume formulas for cylinders, cones, and spheres, offering worksheets, practical examples, and helpful tips to make mastering these concepts as straightforward as possible.
Understanding Cylinder Volume


A cylinder is defined by its height and base, which forms a circle. The volume V of a cylinder can be found using the formula:
V = πr2h
- π (pi) - Approximately 3.14159
- r - The radius of the base circle
- h - The height of the cylinder
Worksheet for Cylinder Volume

Let's practice with the following examples:
| Radius (cm) | Height (cm) | Volume (cm³) |
|---|---|---|
| 5 | 10 | Unknown |
| 3 | 8 | Unknown |
| 2 | 6 | Unknown |

Calculate the volume for each row. The solution for the first row is:
V = π * (5)2 * 10 = 785.398 cm³
🔍 Note: For more precise calculations, consider using more decimal places for π or use a calculator with a built-in π function.
Exploring Cone Volume


Cones, unlike cylinders, taper from a circular base to a point. Their volume V is calculated with:
V = (1/3) * πr2h
- π (pi) - Approximately 3.14159
- r - The radius of the base circle
- h - The height from the base to the apex of the cone
Worksheet for Cone Volume
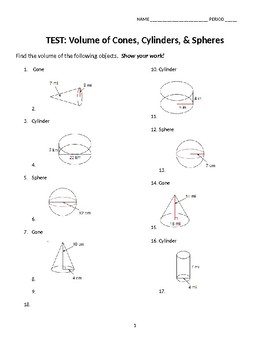
Practice calculating the volume of cones with the following dimensions:
| Radius (cm) | Height (cm) | Volume (cm³) |
|---|---|---|
| 4 | 15 | Unknown |
| 6 | 12 | Unknown |
| 3 | 8 | Unknown |
Here's how to solve the first row:
V = (1/3) * π * (4)2 * 15 = 251.327 cm³
Determining Sphere Volume


Spheres, being perfectly symmetrical, have a simpler volume formula:
V = (4/3) * πr3
- π (pi) - Approximately 3.14159
- r - The radius of the sphere
Worksheet for Sphere Volume

Try calculating the volume of these spheres:
| Radius (cm) | Volume (cm³) |
|---|---|
| 2 | Unknown |
| 5 | Unknown |
| 7 | Unknown |
Let's solve the first example:
V = (4/3) * π * (2)3 = 33.510 cm³
Exploring volume calculation for cylinders, cones, and spheres not only develops your spatial and mathematical skills but also enhances your ability to appreciate the real-world applications of geometry. From designing containers to understanding fluid dynamics, these shapes play a critical role in numerous fields.
In this journey through geometric volumes, we've:
- Learned the specific volume formulas for cylinders, cones, and spheres
- Engaged with practical worksheets to reinforce understanding
- Discussed how to apply these calculations in everyday scenarios
Remember that mastering these calculations can be immensely satisfying and useful. Keep practicing, and don't shy away from challenging yourself with different dimensions and more complex shapes.
Why does the cone have a volume of one-third the cylinder?

+
The cone’s volume being one-third of the cylinder with the same base and height arises from Cavalieri’s principle, which explains how if two solids have the same cross-sectional area at every height, their volumes will be proportional to their heights. However, the cone’s cross-sectional area decreases as you move up, making its volume one-third that of a similar cylinder.
Can you derive the volume formula for a sphere?

+
The volume formula for a sphere can be derived through calculus, by integrating the volume of an infinitesimally thin disk. Alternatively, using Archimedes’ method of exhaustion, one can approximate the sphere’s volume by inscribing and circumscribing spheres with polyhedra.
What are some real-life applications of these volume calculations?

+
Volume calculations are crucial in many areas:
- Construction and Architecture: Calculating the amount of material needed or the capacity of structures.
- Manufacturing: Determining the amount of material required to produce parts like fuel tanks or spherical containers.
- Biology: Estimating the volume of cells or other biological structures.
- Physics and Engineering: Understanding pressure distribution within enclosed systems or fluid mechanics.



