5 Tips for Mastering Quadratic Functions Graphs

In algebra, understanding how to graph quadratic functions is not just a requirement for academic assessments but also an essential tool for various real-world applications, from engineering to finance. Quadratic functions, represented by the general form y = ax² + bx + c, yield graphs that are parabolas, which can tell us a lot about the behavior of the underlying mathematical model. Here are five detailed tips to help you master graphing quadratic functions effectively:
Understanding the Basics

Before diving into complex graphing techniques, you must grasp the basic concepts:
- The Parabola: A quadratic function graph always forms a U-shaped curve known as a parabola.
- Vertex: The vertex of a parabola indicates either the minimum or maximum point of the graph.
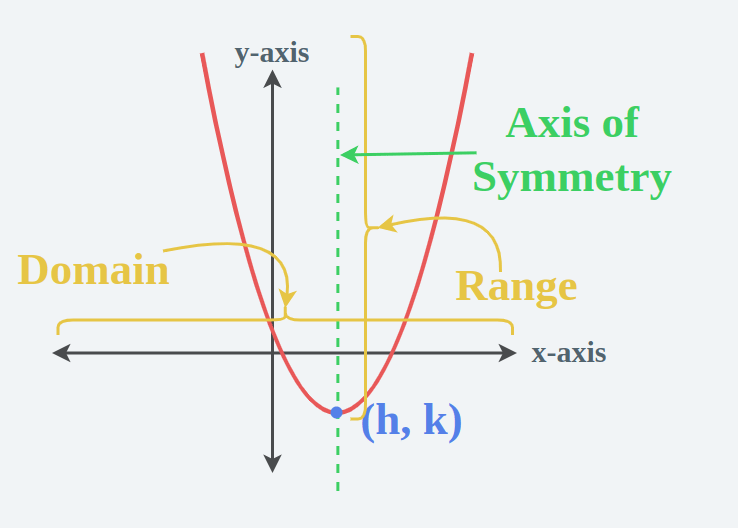
- Axis of Symmetry: Every parabola has an axis of symmetry that runs through its vertex.
To illustrate these basics, consider the function y = x², where the graph will be a parabola opening upwards with its vertex at (0,0) and its axis of symmetry along the y-axis.
Using Vertex Form for Precision

Switching to vertex form, y = a(x-h)² + k, can dramatically simplify the process of graphing quadratic functions:
- (h, k) represents the vertex of the parabola.
- The value of a determines the direction and width of the parabola. If a is positive, the parabola opens upwards; if negative, it opens downwards.
🔑 Note: Using vertex form eliminates the need to complete the square, making it quicker to find the vertex.
Identifying Key Points

Graphing a quadratic function involves identifying key points that define its shape:
| Key Point | Description |
|---|---|
| Vertex | Highest or lowest point on the graph, crucial for determining the parabola’s orientation. |
| Intercepts | The x-intercepts show where the parabola crosses the x-axis, often solved by the quadratic formula. The y-intercept is the value of c in standard form. |
| Roots or Zeros | Points where the parabola intersects the x-axis, these are solutions to the equation when set equal to zero. |

Determining Direction and Shape
The value of a in the quadratic function equation has a significant impact on the graph:
- If a > 0, the parabola opens upwards, reaching a minimum value at its vertex.
- If a < 0, it opens downwards, with a maximum at the vertex.
- The greater the absolute value of a, the narrower the parabola; conversely, the smaller the value, the wider it is.
Mastering Transformations

Transformations on quadratic functions can shift, stretch, or reflect the graph:
- Shifts: Adding or subtracting constants to x or y in the equation shifts the parabola horizontally or vertically.
- Stretching: Multiplying a by a scalar affects the graph’s vertical scale.
- Reflections: Multiplying the entire function by -1 flips the parabola over the x-axis.
Consider y = (x-2)² + 3 as an example. This function shifts the vertex of y = x² 2 units to the right and 3 units up.
In conclusion, mastering quadratic function graphs requires an understanding of the underlying principles, effective use of vertex form, identification of key points, awareness of how the function's coefficients influence the graph, and knowledge of how transformations can alter the parabola. With these tips in mind, you'll find graphing quadratic functions not only manageable but also insightful, helping you predict and understand the behavior of various mathematical and physical phenomena.
How do I find the vertex of a quadratic function?

+
The vertex of a quadratic function y = ax² + bx + c can be found using the formula x = -b/(2a). Substitute this x-value back into the equation to find the corresponding y-value.
What does the axis of symmetry mean?

+
The axis of symmetry for a quadratic function is a vertical line that divides the parabola into two mirror images. It can be found using the vertex formula where its x-coordinate is x = -b/(2a).
How can I graph a quadratic function without using vertex form?

+
You can graph a quadratic function in standard form by finding the vertex through completing the square or using the vertex formula. Then, plot the vertex and a few other points by substituting x-values into the function to find y-values.