Master Cones: Free Volume Worksheet for Math Learners

Mathematics is not just about numbers and equations; it's about understanding the concepts that govern the world around us. One such fundamental concept in geometry is the cone, a three-dimensional geometric shape with a circular base and a smooth curve surface, which narrows to meet at an apex. Understanding cones involves comprehending both their properties and applications, which can be beautifully explored through educational tools like volume worksheets.
Understanding Cones

Cones, with their characteristic shape, are intriguing because they appear in various everyday scenarios:
- Cone-shaped structures: Ice cream cones, traffic cones, and even some architectural marvels.
- Nature: Pine cones, tornadoes, and other natural formations.
- Technology and science: Telescopes, antennas, and spacecraft design.
These real-life applications highlight why understanding cones is crucial. Let's delve into the properties of cones, which can be calculated and understood through volume worksheets:
Volume of a Cone

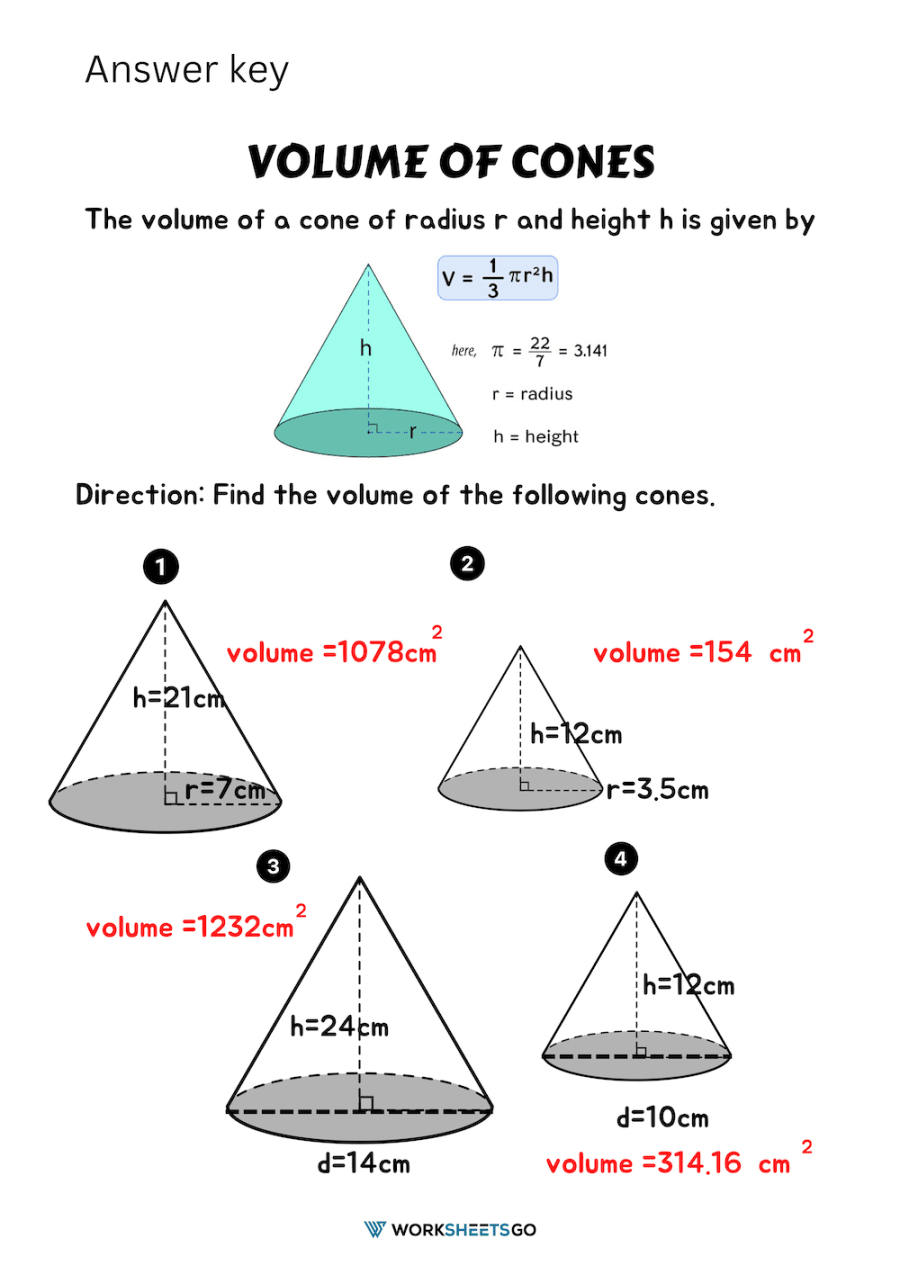
The volume V of a cone is given by the formula:
\[ V = \frac{1}{3} \pi r^2 h \]- r is the radius of the base.
- h is the height of the cone from the base to the apex.
🔎 Note: This formula assumes a right circular cone, where the axis passes through the center of the base.
Volume Worksheets: A Practical Approach

Volume worksheets provide a practical method for learning about cones by:
- Introducing students to the volume formula.
- Offering real-world problems to apply the formula.
- Enhancing mathematical problem-solving skills.
Here are steps to effectively use volume worksheets:
Step-by-Step Guide to Using Volume Worksheets
- Introduction: Begin with an overview of cones, their relevance, and the formula for their volume.
- Problem Selection: Choose problems that range from simple to complex to accommodate different learning levels.
- Worksheet Design:
- Include diagrams or sketches to visualize the cones.
- Clearly state the values of ( r ) and ( h ).
- Provide space for calculations.
- Practice: Have students work through the problems, applying the formula and performing the necessary calculations.
- Verification: Allow time for students to check their answers using a calculator or by comparing with classmates.
- Discussion: Facilitate a group discussion on different approaches to solving the problems.
- Extension: Pose questions that require students to conceptualize and calculate volumes of irregular or composite shapes involving cones.
📚 Note: Encourage students to check their understanding by comparing their results with provided solutions or alternative methods of solving.
Benefits of Using Volume Worksheets
The use of volume worksheets extends beyond mere calculations:
- Visualization: Students gain a visual understanding of three-dimensional shapes.
- Application: They learn to apply formulas in varied contexts.
- Analytical Thinking: Encourages students to think about how changes in radius or height affect volume.
- Communication Skills: Through group work, students enhance their ability to explain mathematical concepts.
Below is a simple table showcasing how changes in the radius and height affect the volume of a cone:
| Radius | Height | Volume |
|---|---|---|
| 1 cm | 3 cm | 3.14 cm3 |
| 2 cm | 3 cm | 12.56 cm3 |
| 3 cm | 3 cm | 28.26 cm3 |
| 3 cm | 6 cm | 56.52 cm3 |

Integrating Cone Volume into Educational Curricula

Worksheets on cone volumes can be seamlessly integrated into educational curricula:
- Mathematics Classes: Teaching geometry, algebra, and problem-solving.
- Science: Introducing principles of volume, density, and displacement.
- Engineering and Architecture: Understanding the strength and design aspects of conic structures.
Here are some educational activities to integrate volume worksheets:
Activity Ideas
- Measure and Calculate: Students measure real objects, estimate their volumes, and then calculate using the formula.
- Design Challenge: Students design their own cone-shaped objects, considering both form and function.
- Comparative Study: Comparing the volumes of different cones or other geometric shapes to understand volume relationships.
To wrap up, volume worksheets for cones provide students with an engaging and practical way to learn about three-dimensional geometry. Through these worksheets, students not only master the mathematical concept of volume but also develop critical thinking and problem-solving skills that are applicable in various scientific and engineering fields. They learn to apply the formula V = \frac{1}{3} \pi r^2 h , understand how changes in the dimensions impact the volume, and visualize how mathematical principles relate to real-world objects. With worksheets as their guide, students embark on a journey to better comprehend the intricate beauty of geometry, enhancing their mathematical proficiency and setting a solid foundation for more advanced studies.
What is the difference between the volume of a cone and a cylinder?
+
The key difference lies in their formula. For a cone, volume is ( V = \frac{1}{3} \pi r^2 h ), while for a cylinder, it’s ( V = \pi r^2 h ). Thus, a cone has one-third the volume of a cylinder with the same base and height.
Can volume worksheets be used for other shapes besides cones?

+
Yes, volume worksheets are versatile tools that can be applied to various geometric shapes like spheres, pyramids, prisms, and even irregular shapes to teach volume calculation and problem-solving skills.
How can teachers assess student understanding using volume worksheets?
+
Teachers can assess understanding through worksheets by checking for correct formula application, error analysis in students’ calculations, and problem-solving approaches in increasingly complex scenarios. Discussions also help gauge conceptual grasp.
What are some common mistakes students make when calculating the volume of a cone?

+
Students often forget the factor of (\frac{1}{3}) in the formula, mix up units of measurement, or fail to square the radius correctly.


