5 Tricks to Solve Angle Measure Worksheet Answers

Unveiling the Secrets: 5 Clever Tricks to Tackle Angle Measure Worksheet Answers
Angles, a fundamental aspect of geometry, can sometimes present a challenge when it comes to worksheets. However, with the right tricks, you can turn this challenging task into an opportunity for quick and accurate problem-solving. Let's dive into some strategies that can help you efficiently navigate through any angle measure worksheet.
1. Understand the Basics of Angles

Before you start solving any worksheet, having a solid grasp of basic angle definitions is crucial:
- Acute Angles: Less than 90°
- Right Angles: Exactly 90°
- Obtuse Angles: Between 90° and 180°
- Straight Angles: Exactly 180°
- Reflex Angles: Between 180° and 360°
Knowing these basic types of angles will help you instantly categorize any angle, which is particularly useful when dealing with multiple choice or fill-in-the-blank questions.
2. Use the Angle Sum Property
One of the most powerful tools in your toolkit is the angle sum property of a triangle. The sum of the angles in any triangle always equals 180°. Here's how you can leverage this:
- When given two angles of a triangle, subtract their sum from 180° to find the third angle.
- If a problem involves external angles or involves angles around a point, remember that angles around a point sum to 360°.
This trick not only simplifies the calculation but also reduces the chance of arithmetic errors.
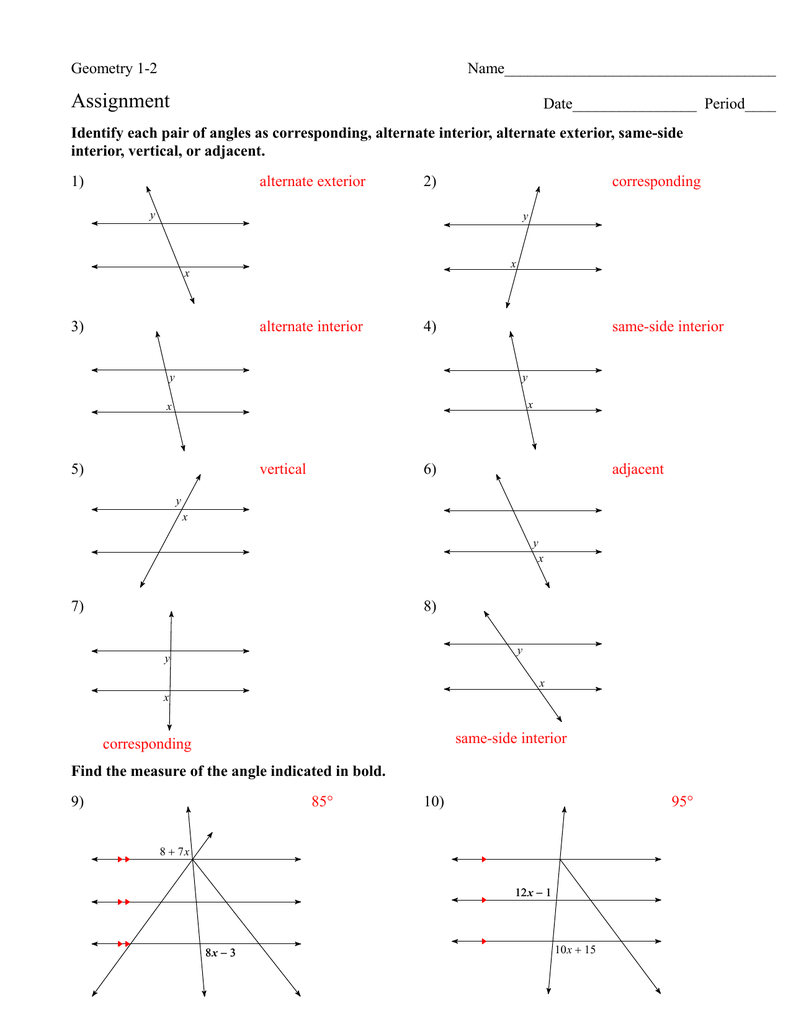
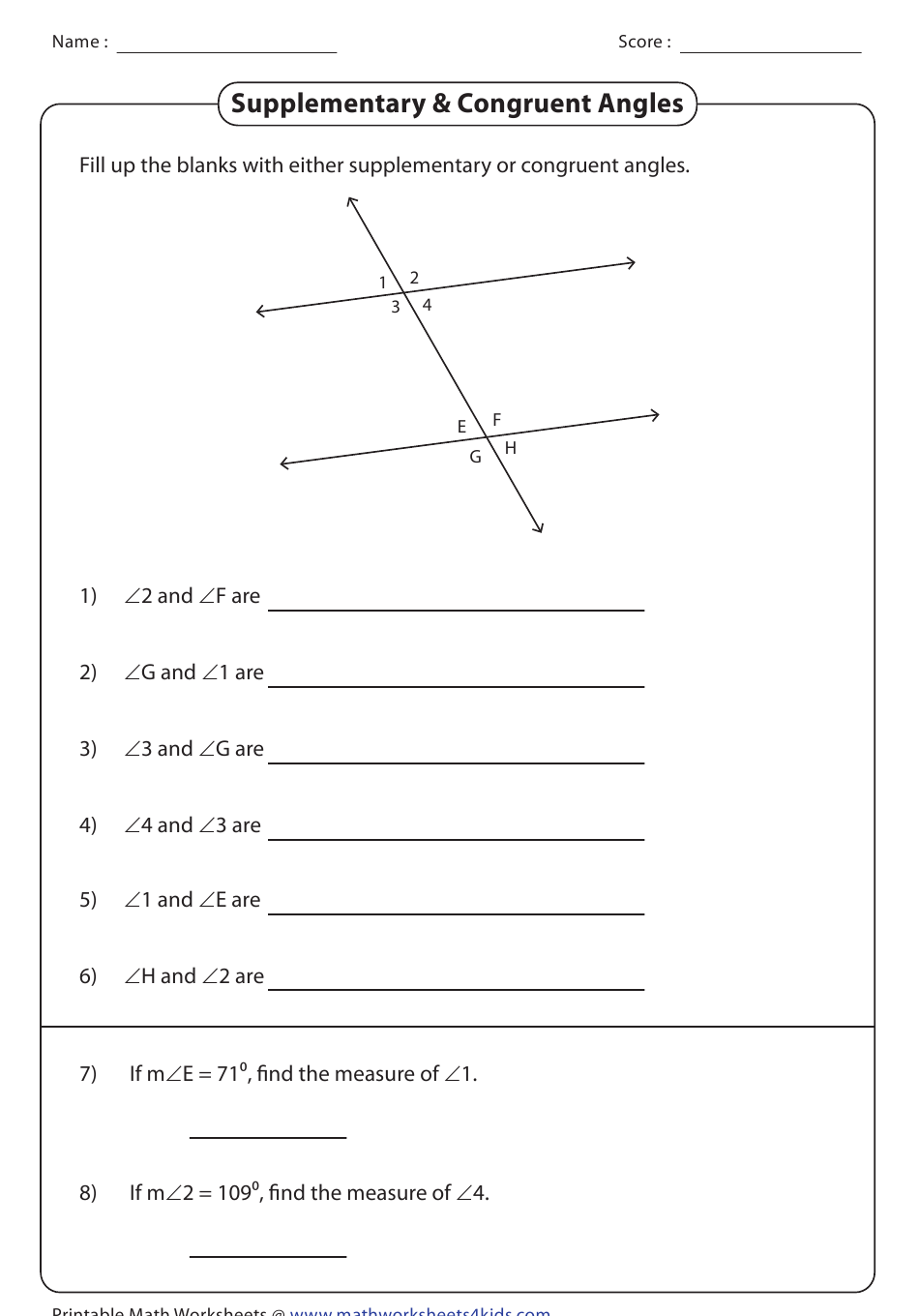
3. Recognize Angle Relationships

Angles in worksheets often come with special relationships:
- Adjacent Angles: Angles that share a vertex and a side but do not overlap.
- Complementary Angles: Two angles whose measures add up to 90°.
- Supplementary Angles: Two angles whose measures add up to 180°.
- Vertical Angles: Opposite angles formed by intersecting lines are congruent.
Recognizing these relationships can allow you to solve for unknown angles without having to calculate every angle from scratch. Here's an example in a table:
| Angle Pair | Relationship | If One Angle is Given |
|---|---|---|
| Complementary | Sum = 90° | Subtract the given angle from 90° |
| Supplementary | Sum = 180° | Subtract the given angle from 180° |
| Vertical | Congruent | Use the given angle as the answer for the unknown angle |

By understanding these relationships, you can quickly deduce the values of other angles in the worksheet.
4. Employ the Use of Geometry Rules

Geometry is filled with rules that can simplify complex problems:
- Isosceles Triangles: Two sides equal, base angles equal.
- Equilateral Triangles: All sides and angles are equal (60°).
- Parallelograms: Opposite angles are equal, and consecutive angles sum to 180°.
- Central Angles of a Circle: Angle measure equals arc measure.
Knowing when to apply these rules can drastically reduce your computation time.
📝 Note: These geometric properties not only apply to basic shapes but are also critical when dealing with more complex figures like polygons.
5. Pattern Recognition and Estimation

Sometimes, rather than calculating each angle precisely, recognizing patterns or estimating can be equally effective:
- Look for symmetry in diagrams to identify congruent angles or to quickly estimate angles.
- In cases where exact calculation isn't necessary, use mental arithmetic or known angle measures to estimate unknown angles.
This technique is invaluable when dealing with large sets of data or when time is of the essence during exams.
Summing It Up

Navigating through an angle measure worksheet becomes much more manageable when armed with the right strategies. From understanding angle basics to employing geometry rules, these tricks help simplify complex problems. Remember, the key lies not just in calculation but also in recognizing patterns and relationships between angles. By practicing these strategies, you'll find that solving angle measure questions becomes second nature, transforming what might have been a tedious task into an engaging exercise.
What is the difference between adjacent and vertical angles?

+
Adjacent angles share a common vertex and a common side but do not overlap, while vertical angles are opposite angles formed by intersecting lines and are congruent.
How do I find the measure of an unknown angle in a triangle?

+
If two angles are given in a triangle, subtract their sum from 180° to find the third angle. This is based on the angle sum property of a triangle, where the sum of all three angles equals 180°.
Why is it useful to recognize the type of angles?

+
Recognizing the type of angles helps categorize them quickly, which can streamline the solving process, especially in multiple choice or standardized test settings.
Can I use these tricks for any geometry worksheet?
+
While these tricks are primarily focused on solving angle measures, the principles of pattern recognition, angle relationships, and basic geometry rules apply widely in various geometry problems.
Is it better to estimate or calculate precisely?

+
The choice depends on the context. For exact answers or when dealing with small angles, precise calculation is necessary. For larger angles or when time is limited, estimation based on patterns or known measures can be faster and still accurate enough for certain purposes.



