5 Must-Know Two-Step Inequality Word Problems Solved

Introduction to Two-Step Inequality Word Problems

In mathematics, word problems serve as a bridge between abstract numerical operations and their practical application. Among the many types of word problems, two-step inequality word problems are particularly important as they integrate algebraic manipulation with real-world scenarios. This comprehensive guide will walk you through five essential two-step inequality word problems, providing a step-by-step solution to each, and shedding light on common pitfalls, strategies for solving, and key insights to aid your learning.

Problem 1: The Movie Ticket Scenario

Samantha has $40 to spend at the movies. She wants to buy tickets, where each ticket costs $12, and also plans to buy a large popcorn for $6. How many tickets can Samantha buy while still being able to afford the popcorn?

Solving the Problem

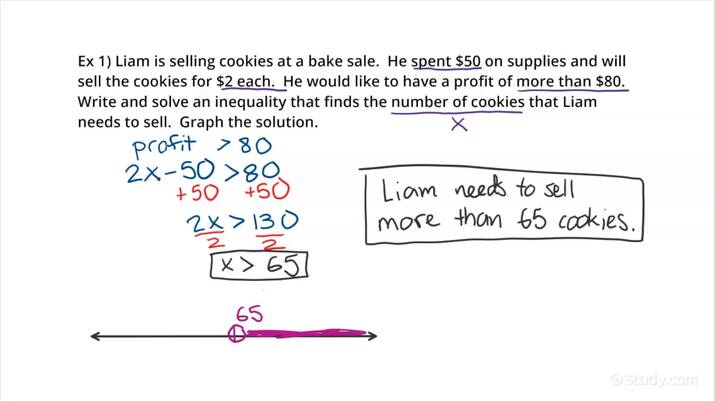
1. Set up the inequality: Let ( t ) represent the number of tickets Samantha can buy. The total cost of tickets and popcorn must not exceed $40:

   [ 12t + 6 \leq 40 ]

2. Simplify: Subtract 6 from both sides:

   [ 12t \leq 34 ]

3. Solve for ( t ): Divide both sides by 12:

   [ t \leq \frac{34}{12} \approx 2.83 ]

   Since Samantha can only buy whole tickets:

💡 Note: When dealing with inequalities involving whole numbers, you should round down to the nearest whole number to ensure the solution fits the scenario.

Therefore, Samantha can buy at most 2 tickets while still being able to afford the popcorn.

Problem 2: The Fitness Tracker Plan

Jake wants to buy a fitness tracker priced at $130, but he can only spend a maximum of $150 on fitness equipment this month. How much more can he spend on other fitness accessories?

Solving the Problem

1. Set up the inequality: Let ( x ) represent the additional amount Jake can spend. The total spending on the fitness tracker and additional equipment must not exceed $150:

   [ 130 + x \leq 150 ]

2. Simplify: Subtract 130 from both sides:

   [ x \leq 20 ]

Jake can spend up to $20 on other fitness accessories.

Problem 3: The Plant Watering Dilemma

A local gardener can only spend 2 hours a day on her tasks. She estimates that watering her plants takes about 1 hour. How many additional tasks can she perform in the remaining time if each task takes 15 minutes?

Solving the Problem

1. Set up the inequality: Let ( t ) be the number of additional tasks. The time for watering and tasks must not exceed 2 hours (120 minutes):

   [ 60 + 15t \leq 120 ]

2. Simplify: Subtract 60 from both sides:

   [ 15t \leq 60 ]

3. Solve for ( t ): Divide by 15:

   [ t \leq 4 ]

The gardener can perform up to 4 additional tasks after watering the plants.

Problem 4: The Pizza Party Puzzle

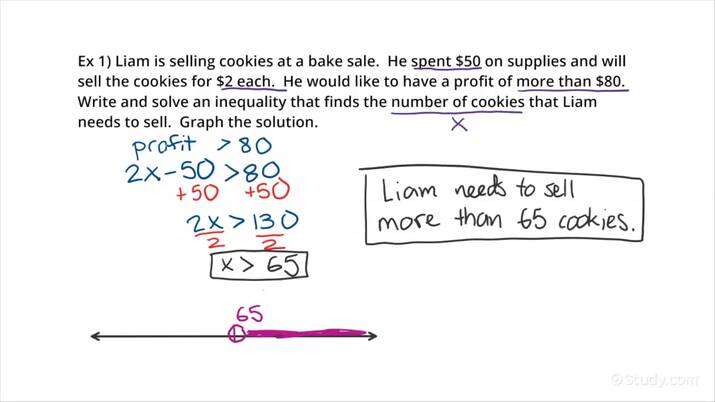
Kendra is organizing a pizza party for her friends. Each pizza costs $12, and she has $100. She needs to save at least $10 for snacks and drinks. How many pizzas can she buy for the party?

Solving the Problem

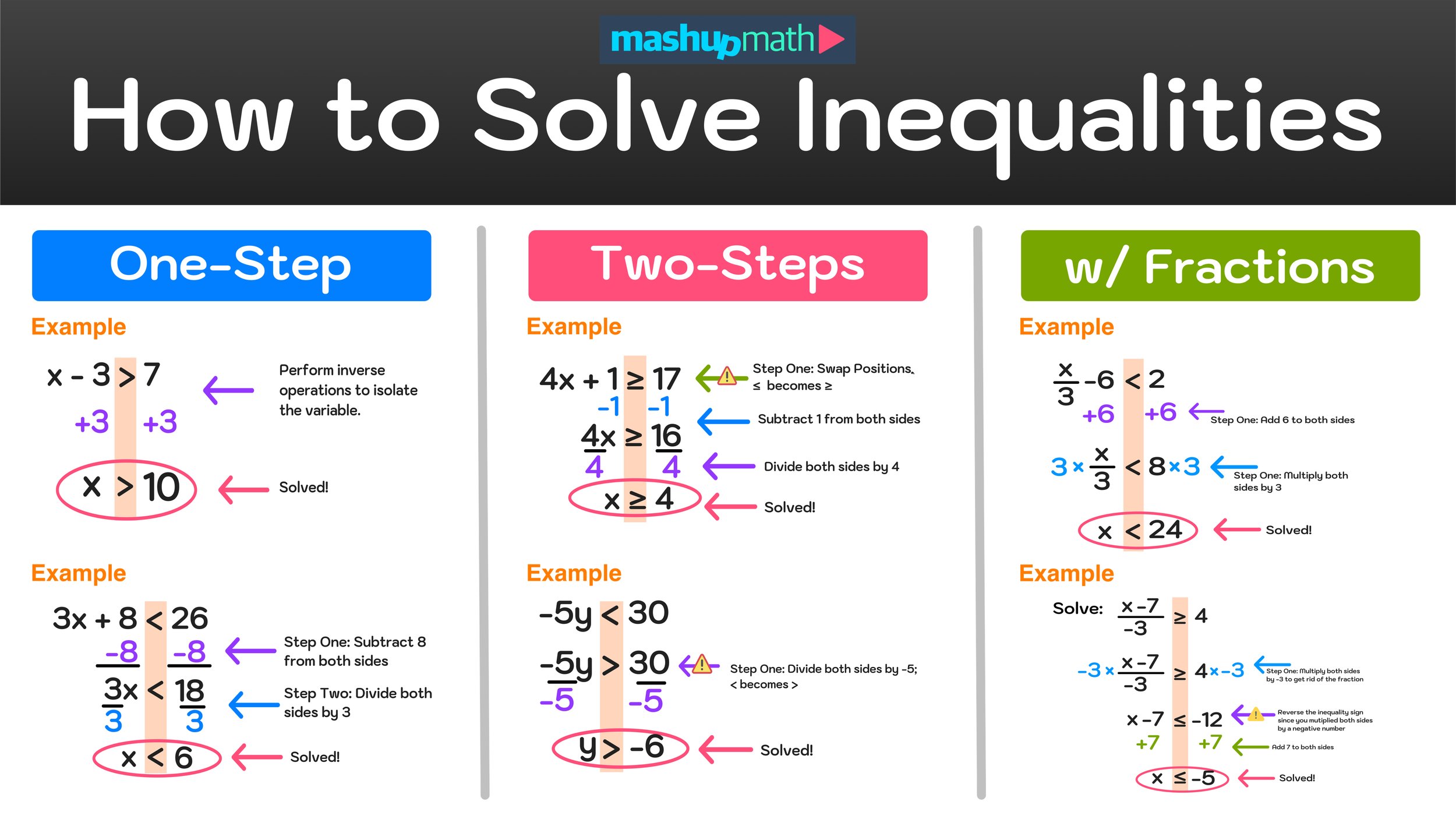
1. Set up the inequality: Let ( p ) represent the number of pizzas. The cost for pizzas and snacks must not exceed 100, minus the 10 Kendra wants to save:

   [ 12p \leq 90 ]

2. Solve for ( p ): Divide by 12:

   [ p \leq 7.5 ]

Kendra can buy at most 7 pizzas while still having enough money for snacks.

Problem 5: The Battery Charging Time

A phone's battery is currently at 25%. It charges at a rate of 15% per hour. If fully charged, how many more hours does the phone need to charge?

Solving the Problem

1. Set up the inequality: Let ( h ) be the number of hours needed. The battery must reach 100% from 25%:

   [ 15h + 25 \geq 100 ]

2. Simplify: Subtract 25 from both sides:

   [ 15h \geq 75 ]

3. Solve for ( h ): Divide by 15:

   [ h \geq 5 ]

The phone needs at least 5 more hours to fully charge.

🔍 Note: When dealing with fractions or decimals in practical problems, always round up for quantities like charging time, as partial hours are not practical in this context.

Recapitulation

We’ve explored five distinct scenarios where two-step inequalities play a crucial role in solving real-life problems. From budgeting for movies and fitness gear to managing time and organizing parties, these problems highlight the practical application of algebra. Here are the key takeaways:

• Setting up inequalities based on given conditions is fundamental.
• Simplifying inequalities often involves algebraic operations like addition, subtraction, multiplication, or division.
• Interpreting results correctly, especially when dealing with whole numbers, is essential for practical application.
• Rounding up or down depending on the context of the problem ensures realistic solutions.

Why are inequalities used instead of equations in these word problems?

+

Inequalities allow for a range of possible solutions, which is more reflective of real-world constraints and conditions where exact answers might not always be necessary or possible.

How do you know when to round up or down?

+

It depends on the context. If you’re dealing with a scenario where you cannot exceed a limit, like the number of tickets or pizzas you can buy, round down. For cases where you need at least a certain amount or time, round up.

Can inequalities be applied to any real-life problem?

+

Yes, many real-life scenarios involve limits or constraints, making inequalities the perfect mathematical tool to model these conditions.