5 Essential Tips for Algebra and Geometry Problem Solving

Are you grappling with algebra and geometry problems in school or on your own learning path? Mastering the concepts of algebra and geometry not only opens doors to understanding advanced mathematics but also sharpens your analytical and logical reasoning skills. Here, we'll explore five essential tips that can transform your approach to solving problems in these fascinating fields of math.
Understanding the Problem Statement Clearly
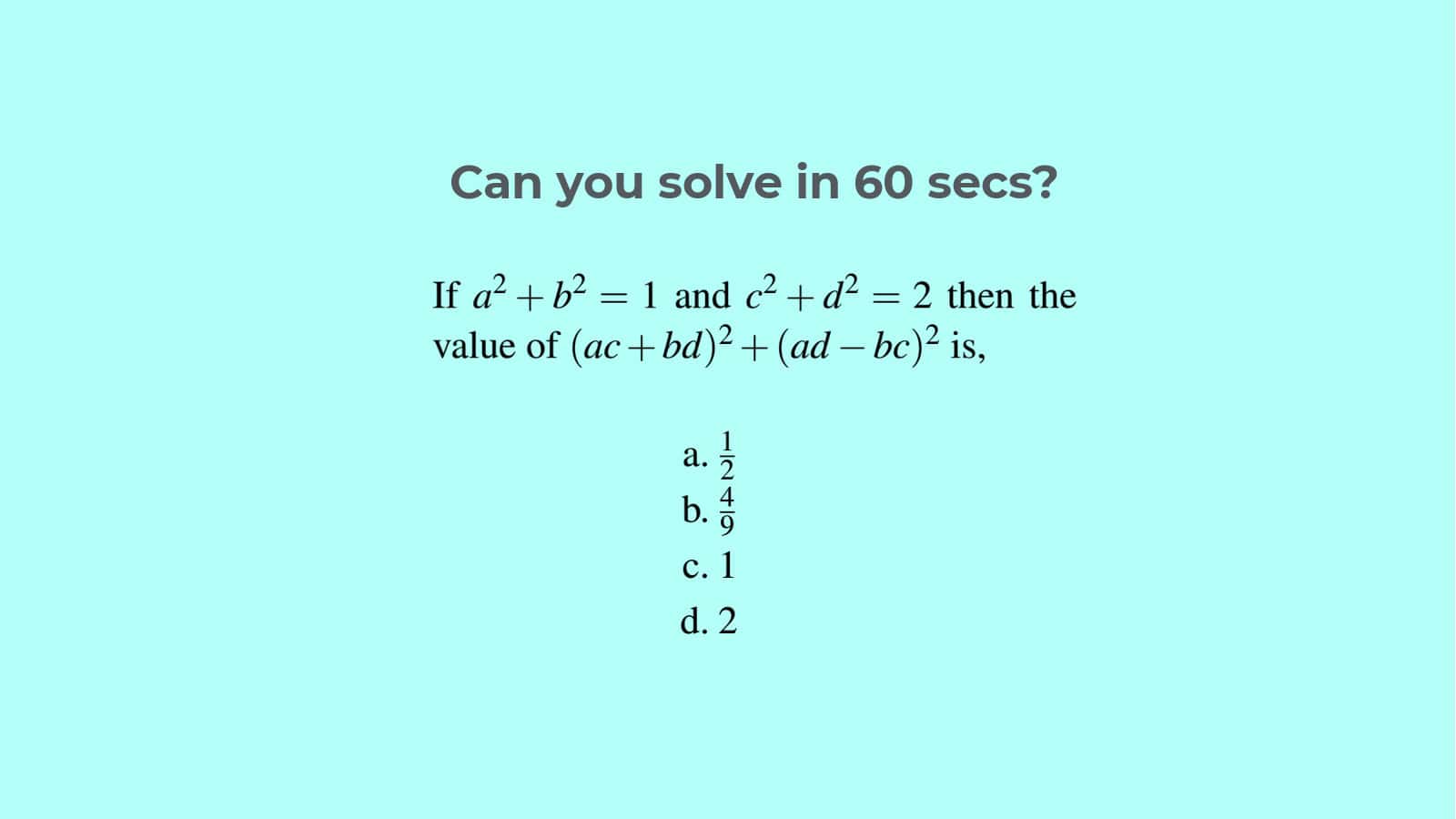
When approaching an algebra or geometry problem, the first crucial step is to understand what the problem is asking. Here’s how to achieve clarity:
- Read Twice: Always read the problem at least twice. The first read gives you an overview, while the second allows you to catch details you might have missed.
- Visualize: Draw diagrams or pictures if it’s a geometry problem, or jot down the equations if it’s algebra. Visual aids can significantly clarify complex problems.
- Break it Down: Complex problems often contain multiple smaller problems. Identify these and tackle them one by one.
- Ask ‘What If’: Sometimes considering hypothetical scenarios can give insights into what the problem is asking.
Develop a Systematic Approach

Mathematics is about structure and logic. Here’s how to organize your problem-solving:
- List Knowns and Unknowns: Determine what you know from the problem statement and what you need to find out.
- Choose a Strategy: Pick a method to solve the problem, whether it’s solving equations, drawing geometric constructions, or using algebraic rules.
- Work Backwards: For problems where the answer is given, working backwards can often reveal the steps to solve for unknown variables.
- Use Proof by Contradiction: If direct methods fail, consider proving the problem by assuming the opposite of what you need to prove.
🔍 Note: Sometimes, mathematical problems can be solved in more than one way. Learning multiple strategies increases your flexibility in problem-solving.
Effective Use of Equations and Formulas

Algebra and geometry involve manipulating equations and applying formulas. Here are key strategies:
- Know Your Formulas: Memorize essential formulas for area, volume, trigonometry, and algebraic identities.
- Substitution: Replace variables with given values or other expressions to simplify equations.
- Solve for a Variable: Use techniques like isolating the variable or using inverse operations to solve for the unknown.
- Recognize Patterns: Look for algebraic or geometric patterns that can guide your solution strategy.
| Equation/Formula | Description |
|---|---|
| Area of Circle: A = πr² | Where A is the area and r is the radius |
| Pythagorean Theorem: a² + b² = c² | Relationship between sides in a right triangle |
| Quadratic Formula: x = (-b ± √(b² - 4ac)) / 2a | For solving quadratic equations in the form of ax² + bx + c = 0 |

Practicing with Real-World Applications

To master algebra and geometry, apply these mathematical principles to real-life scenarios:
- Word Problems: Translate real-life situations into mathematical problems.
- Modeling: Use math to model real-world phenomena, like calculating the area for construction or the trajectory of an object.
- Check the Units: Ensure your answers are consistent with real-world units, which can help you spot errors in your calculations.
- Explore Geometry: Look for patterns in your surroundings; geometry is everywhere, from the shape of rooms to the layout of cities.
🧮 Note: Real-world applications often require estimation and making assumptions, which are good exercises in critical thinking.
Reflecting on Your Mistakes and Learning

The journey to mastering math involves learning from errors:
- Review Your Work: Go through your steps again, looking for mistakes or missed opportunities for simplification.
- Understand the Concept: If you missed the concept, study it again with different sources or explanations.
- Ask for Help: Don’t hesitate to seek assistance from teachers, peers, or online resources.
- Keep a Notebook: Record problems you struggle with, your mistakes, and the correct solutions. This log can be a valuable tool for future reference.
In summary, mastering algebra and geometry requires a mix of understanding the problems, systematic approaches, effective use of equations, real-world application, and continuous learning from mistakes. With these strategies, you'll not only solve problems more efficiently but also deepen your appreciation for the beauty and logic of mathematics.
How can I improve my speed in solving algebra problems?

+
Practice regularly, focus on understanding key concepts, and use shortcuts or algebraic identities to simplify your calculations.
What’s the best way to memorize geometry formulas?

+
Create visual aids, use mnemonic devices, and apply the formulas in various problems to enhance memorization through practice.
Are there any tools or apps that can help with learning algebra and geometry?

+
Yes, numerous educational apps and online platforms like Khan Academy, Mathway, and GeoGebra offer interactive learning tools for algebra and geometry.