5 Essential Tips for Parallel Lines and Transversals Worksheet Answers

Introduction to Parallel Lines and Transversals

The study of geometry often introduces students to concepts that are foundational in understanding spatial relationships. Among these, parallel lines and transversals stand out due to their practical applications and the intriguing theorems they involve. This blog post will dive deep into the topic, providing essential tips for tackling worksheets on parallel lines and transversals, and offering clear answers to common worksheet problems.

Understanding Parallel Lines
Parallel lines are straight lines that never intersect no matter how far they are extended. They run alongside each other, maintaining the same distance at all points. Here’s what you need to know:
- Definition: Lines that are equidistant and do not intersect.
- Properties: The slopes of parallel lines are the same.
- Symbol: They are often denoted with parallel arrows (>>)
The Role of Transversals

A transversal is a line that intersects two or more parallel lines at distinct points. This interaction leads to the formation of various angles:
- Corresponding Angles: Angles in matching corners, created by the transversal and the parallel lines.
- Alternate Interior Angles: Non-adjacent interior angles on opposite sides of the transversal.
- Consecutive Interior Angles: Adjacent angles on the same side of the transversal.
- Vertical Angles: Opposite angles formed by two intersecting lines.

Tips for Solving Parallel Lines and Transversals Worksheets

When facing worksheets on this topic, here are some strategies to help you:
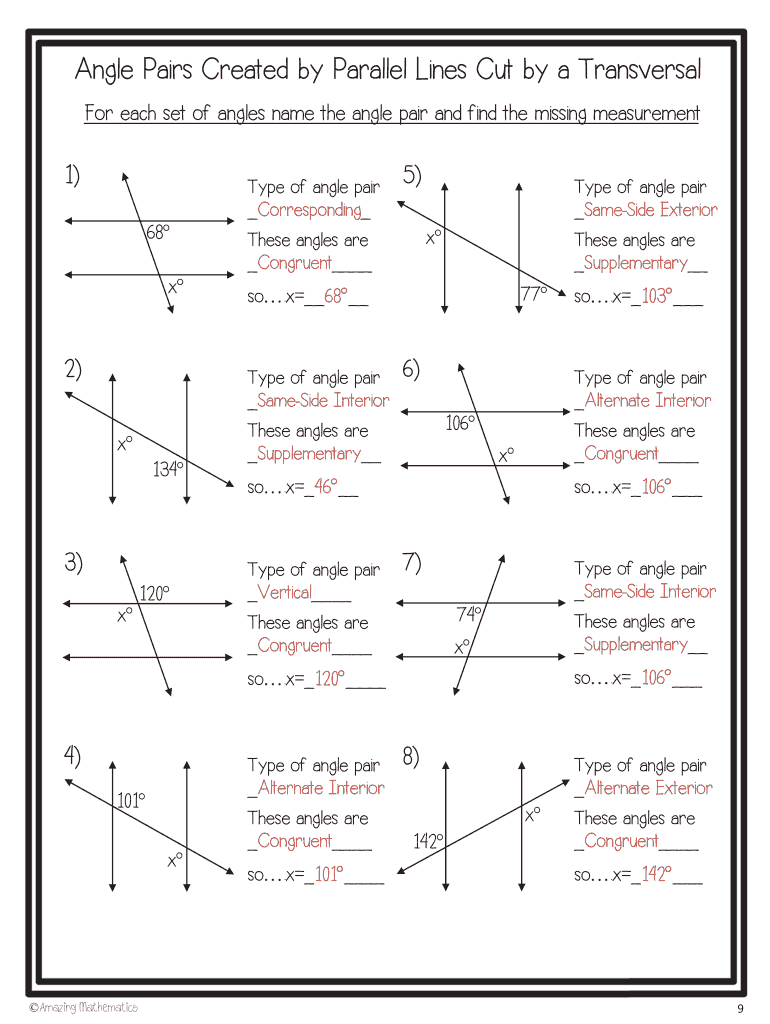
1. Identify the Angles:

- Recognize the different types of angles formed by the transversal and the parallel lines.
- Highlight corresponding, alternate interior, and consecutive interior angles with different colors or symbols to keep track of them.
- Remember, when two parallel lines are cut by a transversal, corresponding angles are congruent, alternate interior angles are congruent, and consecutive interior angles are supplementary.
2. Use Theorems to Find Missing Angles:
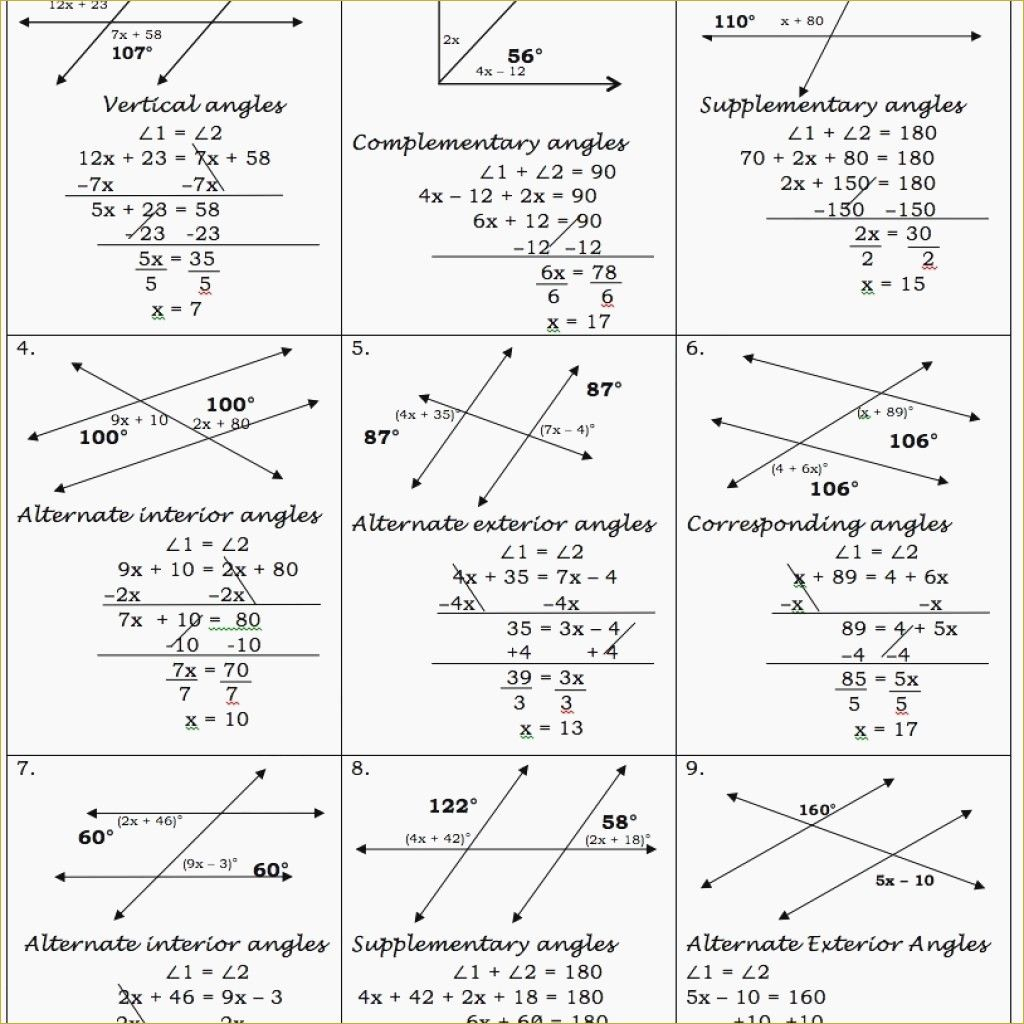
| Theorem | Description |
|---|---|
| Corresponding Angles Postulate | If two parallel lines are cut by a transversal, then corresponding angles are congruent. |
| Alternate Interior Angles Theorem | If two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent. |
| Consecutive Interior Angles Theorem | If two parallel lines are cut by a transversal, then the pairs of consecutive interior angles are supplementary (sum up to 180°). |

3. Set Up Equations for Supplementary Angles:

- When dealing with consecutive interior angles, set up equations that reflect their supplementary nature. For example, if ∠1 + ∠2 = 180°, you can solve for one angle if the other is known.
4. Visualize and Confirm Your Work:

- Draw diagrams if not provided. Visualization helps in understanding the spatial relationship between angles.
- Use a protractor to physically measure angles if possible, to confirm your calculations.
5. Check Consistency:

- Ensure that your angle solutions are consistent with the given information. For instance, if one pair of corresponding angles is congruent, the other pairs should also align with this information.
📝 Note: Always double-check your answers. Geometry can be tricky, and small errors in angle identification can lead to incorrect solutions.
Application of Parallel Lines and Transversals

Understanding these concepts is not just academic; they have real-world applications:
- Architecture: To ensure buildings have straight walls and accurate proportions.
- Navigation: For plotting courses where lines of sight remain constant.
- Railway Design: Tracks must be parallel to maintain stability and safety.
Conclusion

In conclusion, mastering parallel lines and transversals involves recognizing the patterns and relationships these lines and angles form. By applying the tips discussed, students can better navigate the complexities of geometry, solve worksheet problems with confidence, and apply these principles in various practical contexts. This understanding not only aids in academic settings but also enriches one’s perception of spatial relationships in the everyday world.
What are the most common angles formed by transversals?

+
The most common angles formed by transversals include corresponding angles, alternate interior angles, consecutive interior angles, and vertical angles.
Can parallel lines ever meet?
+
In Euclidean geometry, parallel lines never meet no matter how far they are extended. However, in non-Euclidean geometries like spherical geometry, lines can intersect even if they appear parallel from a certain perspective.
How can I remember the different types of angles?

+
Try using acronyms or mnemonics. For example, CAB could stand for “Corresponding Angles are Big” (since they are the same), and AIA for “Alternate Interior Angles are Identical.”



