Unlock Math Success: Trig Ratio Worksheet Solutions

Unlocking the door to mathematical proficiency, especially in the challenging area of trigonometry, can be a game-changer for students at all levels. Trigonometric ratios—sine, cosine, and tangent—are essential tools for solving real-world problems involving angles and distances. This detailed guide will lead you through a series of worksheets focusing on these critical concepts, providing solutions, tips for mastering trigonometric functions, and addressing common student queries.
Understanding Trigonometric Ratios


Trigonometry is the branch of mathematics dealing with the relationships between the sides and angles of triangles. Here’s a brief overview:
- Sine (sin): The ratio of the length of the side opposite to the angle divided by the length of the hypotenuse.
- Cosine (cos): The ratio of the length of the adjacent side divided by the hypotenuse.
- Tangent (tan): The ratio of the length of the side opposite to the angle to the length of the adjacent side.
Basic Definitions

| Function | Definition |
|---|---|
| sin(θ) | Opposite / Hypotenuse |
| cos(θ) | Adjacent / Hypotenuse |
| tan(θ) | Opposite / Adjacent |

📝 Note: Always ensure you are using the correct side of the triangle when applying these ratios.
Step-by-Step Guide to Solving Trigonometric Ratios


Worksheet Example 1: Finding Ratios

Given a right triangle with sides 3, 4, and 5:
- Calculate the sine of the angle opposite to the side of length 3.
- Determine the cosine of the angle adjacent to the side of length 4.
- Find the tangent of the angle opposite the side of length 4.
Solutions
- sin(θ) = 3⁄5 = 0.6
- cos(θ) = 4⁄5 = 0.8
- tan(θ) = 3⁄4 = 0.75
Worksheet Example 2: Applying Ratios in Real-Life Scenarios

Suppose you’re standing at the top of a building trying to measure the height of a tree:
- Measure the angle of elevation to the top of the tree, which is 35 degrees.
- You are 10 meters away from the base of the tree.
- Use trigonometry to find the height of the tree.
Solutions
Using tan(35°) = height/10:
- height = tan(35°) * 10 ≈ 1.43 * 10 ≈ 14.3 meters
📝 Note: For real-world applications, always take into account factors like the height of your eyes and any obstructions.
Common Challenges and Solutions

Confusing Opposite, Adjacent, and Hypotenuse
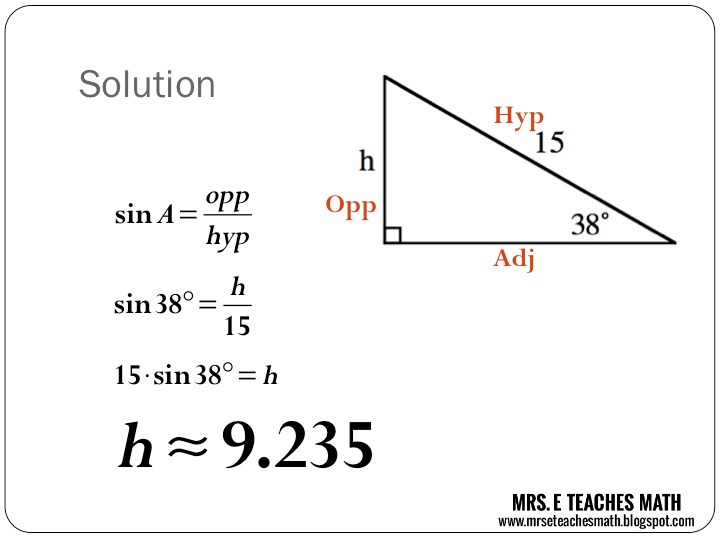
A common mistake students make is misidentifying which side is the opposite, adjacent, or hypotenuse relative to the angle they’re working with. Here’s how to avoid this:
- Label the sides clearly.
- Draw a diagram to visualize the problem.
- Use mnemonic devices like SOH-CAH-TOA to remember the definitions.
Calculator Errors

Using calculators for trigonometric calculations can sometimes lead to errors. Here are some tips:
- Ensure your calculator is set to degrees or radians as required.
- Double-check the mode (inverse or direct) before using sine, cosine, or tangent functions.
- Understand the limitations of calculator precision for more complex problems.
In Summary

Navigating through trigonometry might seem daunting at first, but with practice and a solid understanding of trigonometric ratios, you can unlock its potential for solving real-world problems. This guide has provided insights into understanding sine, cosine, and tangent, along with practical examples to illustrate their application. Remember to keep your labels clear, use visual aids, and check your calculations to avoid common pitfalls.
Why are trigonometric ratios important?

+
Trigonometric ratios help in measuring distances, heights, and angles in various fields like engineering, navigation, and surveying. They form the basis of understanding wave patterns, cycles, and periodic phenomena.
How do I remember the ratios?

+
Use mnemonics like SOH-CAH-TOA which stands for Sine is Opposite over Hypotenuse, Cosine is Adjacent over Hypotenuse, and Tangent is Opposite over Adjacent.
What if the triangle isn’t a right triangle?

+
In non-right triangles, we use the Law of Sines or the Law of Cosines to relate sides and angles.