Triangle Sum Theorem: 5 Worksheet Answers Unveiled

The Triangle Sum Theorem, often referred to as the sum of angles in a triangle theorem, states that the sum of the three interior angles in a triangle is always 180 degrees. This fundamental principle is key for students learning geometry and those who are preparing for geometry exams or solving geometry-related problems. Here, we will delve into understanding this theorem and unveil 5 worksheet answers for additional practice.
Understanding the Triangle Sum Theorem


The Triangle Sum Theorem is a cornerstone in geometry because it allows us:
- To determine unknown angles in a triangle.
- To confirm the accuracy of given angles.
- To explore relationships between angles in complex shapes.
How to Apply the Theorem

To apply the Triangle Sum Theorem:
- Identify the known angles in the triangle.
- Sum up these angles and subtract from 180 degrees.
- Use the result to find any missing angle.
Worksheet Answers: Exploring the Triangle Sum Theorem

Here are 5 worksheet answers to help solidify your understanding of the Triangle Sum Theorem:
| Problem | Answer |
|---|---|
| If two angles of a triangle are 40° and 60°, what is the third angle? | The third angle is 80° because 180° - (40° + 60°) = 80°. |
| A triangle has angles 50°, 55°, and another unknown angle. What is the unknown angle? | The unknown angle is 75° because 180° - (50° + 55°) = 75°. |
| If one angle of a triangle is 90°, what are the possible ranges for the other two angles? | The sum of the other two angles must be 90° but can be any angles that add up to 90°. |
| A triangle with all angles equal. What is each angle? | Each angle in an equilateral triangle is 60°. |
| If an angle in a triangle is 30° more than another angle, what are the angles? | If we let the smaller angle be x, then the larger angle is x + 30°. The third angle is 180° - 2x - 30°. |
✏️ Note: Remember, an equilateral triangle has all angles equal to 60°. It's a special case where the theorem directly applies.
Extended Applications of the Theorem

The Triangle Sum Theorem isn’t just about triangles; its implications extend:
- To polygons, where it’s used to find the sum of internal angles.
- Within geometry, to prove properties of parallelograms, rhombuses, and other shapes.
- In trigonometric calculations, where knowing angles allows for the determination of side lengths using trigonometric ratios.
Thus, mastering this theorem enhances students' overall understanding of geometric relationships and enables them to tackle more complex geometric problems.
Understanding the Triangle Sum Theorem goes beyond simple memorization; it opens the door to a deeper geometric analysis and problem-solving. By revisiting these problems and ensuring a firm grasp on the principles, students can better prepare for more advanced geometric concepts and improve their problem-solving skills in various scenarios. This foundational knowledge will be valuable not only in academic settings but also in practical applications where angles and shapes are crucial considerations.
Why does the Triangle Sum Theorem only work for planar triangles?

+
The theorem applies to Euclidean plane geometry, where space is flat. In non-Euclidean spaces like spherical or hyperbolic geometry, the sum of angles in a triangle can differ.
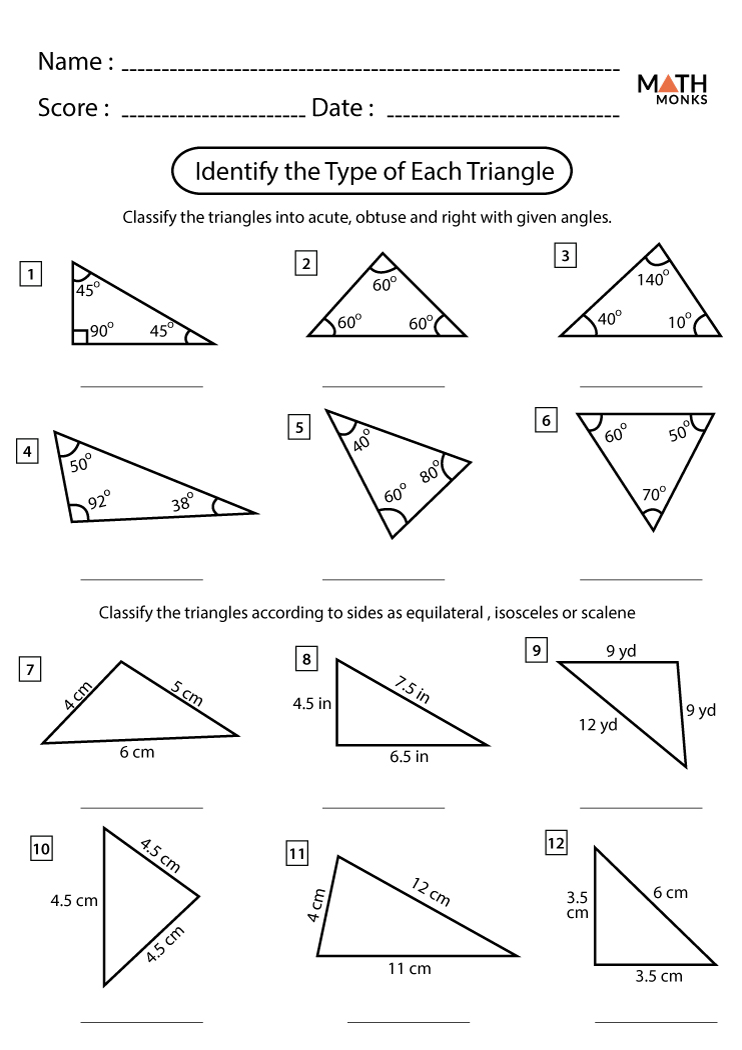
Can the Triangle Sum Theorem help determine if a triangle is acute, right, or obtuse?

+
Yes, by knowing the angles, you can classify the triangle:
- If all angles are less than 90°, it’s acute.
- If one angle is 90°, it’s right.
- If one angle exceeds 90°, it’s obtuse.
How does the theorem relate to exterior angles?

+
An exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles.



