5 Tips for Solving Triangle Sum Problems Easily

When tackling triangle sum problems, many students find themselves stuck. How can you ensure your calculations are both accurate and swift? The answer lies in understanding the fundamentals and applying smart techniques. Here, we'll delve into five tips to help you solve triangle sum problems with ease.
Understand the Basics of Triangle Sum Theorem
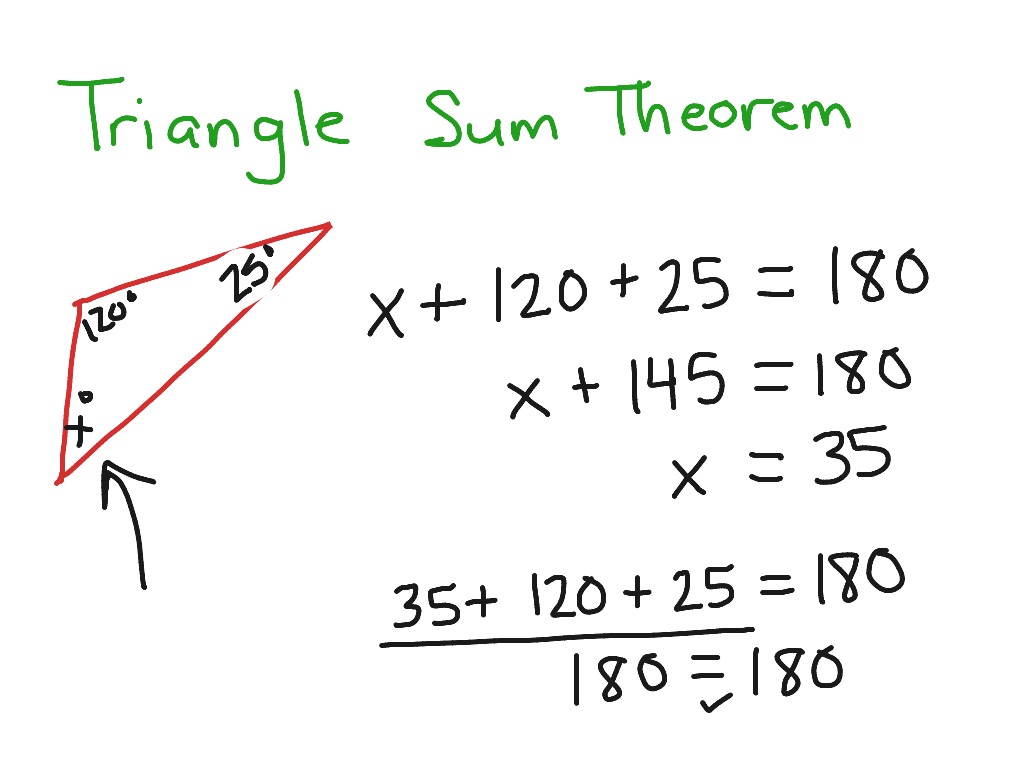
The first step in mastering triangle sum problems is understanding what you’re actually dealing with. The Triangle Sum Theorem states that:
- The sum of the interior angles of any triangle always equals 180 degrees.
Here’s a table to break down the angles:
| Type of Triangle | Angle 1 | Angle 2 | Angle 3 | Sum |
|---|---|---|---|---|
| Equilateral | 60° | 60° | 60° | 180° |
| Isosceles | 40° | 40° | 100° | 180° |
| Scalene | 55° | 65° | 60° | 180° |
🔑 Note: Memorizing this simple fact saves time in calculations.
Identify Triangle Types

Each type of triangle has its own set of characteristics that can make your problem-solving much simpler:
- Equilateral Triangle: All sides and angles are equal. If you know one angle, you know all.
- Isosceles Triangle: Two sides and two angles are equal. Focus on the unequal angle.
- Scalene Triangle: All sides and angles are different, requiring you to solve for each angle individually.
By recognizing the triangle type, you can quickly adapt your approach:
- Check for side equality to classify the triangle.
- Use symmetry in isosceles triangles to simplify calculations.
Use Visual Aids for Problem Solving

Visual aids can significantly aid in understanding and solving triangle sum problems:
- Draw the Triangle: Sketching the triangle helps visualize the angles and apply the theorem more effectively.
- Mark the Known: Highlight given angles or side lengths to keep track of your calculations.
- Use Angles Relationships: Sometimes, one angle’s size can be deduced from the relationships with others, like supplementary angles or complementary angles.
Calculate Sums Logically
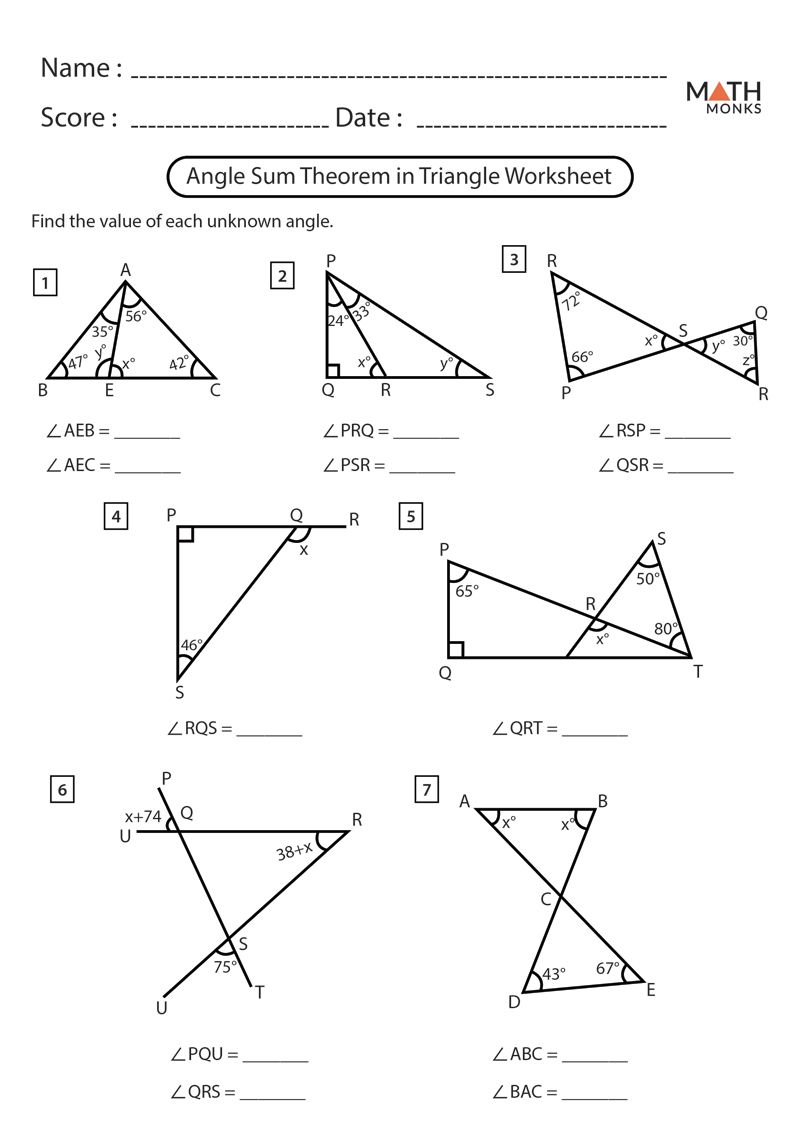
When dealing with the sum of angles in a triangle, ensure you’re following a logical path:
- If two angles are given, subtract their sum from 180° to find the third angle.
- If angles are in algebraic expressions, solve for one variable to find the others. For example, if x + x + 10 + 2x = 180, solve for x and then substitute back.
- Avoid Mistakes: Double-check subtraction and addition, common errors in these calculations.
📝 Note: Remember to consider external angles if problems involve multiple triangles sharing sides.
Be Mindful of Additional Information
Here’s where understanding supplementary information can give you an edge:
- Interior-Exterior Angle Relationships: An exterior angle equals the sum of the opposite interior angles.
- Angles in Inscribed Triangles: In a circle, an inscribed triangle’s opposite angle is half of the intercepted arc.
- Parallelogram or Trapezoid: If triangles are part of these figures, use their known properties to solve for angles.
Always scan the problem for these hidden hints or additional geometric properties:
- Look for congruence or similarity for shortcuts in calculation.
- Check for perpendicular or parallel lines influencing angles.
To become adept at solving triangle sum problems, you need to:
- Master the fundamental principles like the Triangle Sum Theorem.
- Recognize the type of triangle and use its unique properties.
- Employ visual aids to aid in problem comprehension.
- Ensure logical calculations when dealing with sums.
- Make use of additional geometric information to simplify the process.
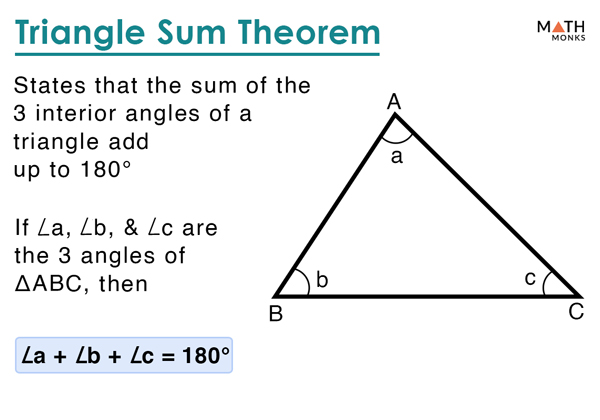
What is the Triangle Sum Theorem?

+
The Triangle Sum Theorem states that the total of the interior angles in any triangle is 180 degrees.
How can identifying triangle types help in solving problems?

+
By identifying the type of triangle, you can use specific properties like angle equality or symmetry to simplify calculations and problem-solving.
Why should I draw the triangle?

+
Visualizing the triangle helps in better understanding the problem’s structure, keeping track of given information, and applying geometric relationships more accurately.



