Slope Intercept Form Worksheet Algebra 1 Solutions

The Basics of Slope Intercept Form

In algebra, the slope intercept form is one of the most commonly used equation forms to represent linear equations. The form is expressed as y = mx + b where:
- m is the slope of the line, indicating how steep the line is.
- b represents the y-intercept, which is the point where the line intersects the y-axis.
This form is exceptionally useful because it directly tells you two fundamental characteristics of a line from its equation:
- The slope (how the line tilts or the rate of change).
- The y-intercept (the starting point of the line on the y-axis).
Why Use Slope Intercept Form?

The slope intercept form is widely used for several reasons:
- It's straightforward for graphing a line on a coordinate plane.
- It clearly indicates the line's behavior, making it easy to understand how the line changes.
- Transformations between different forms of linear equations (like point-slope form or standard form) are simpler with this form.
Key Components of Slope Intercept Form

| Component | Description | Example |
|---|---|---|
| Slope (m) | The ratio of vertical change (rise) to the horizontal change (run). | If m = 2, for every 1 unit increase in x, y increases by 2 units. |
| y-Intercept (b) | The point at which the line intersects the y-axis; the value of y when x is 0. | If b = 3, the line crosses the y-axis at point (0, 3). |

Graphing with Slope Intercept Form
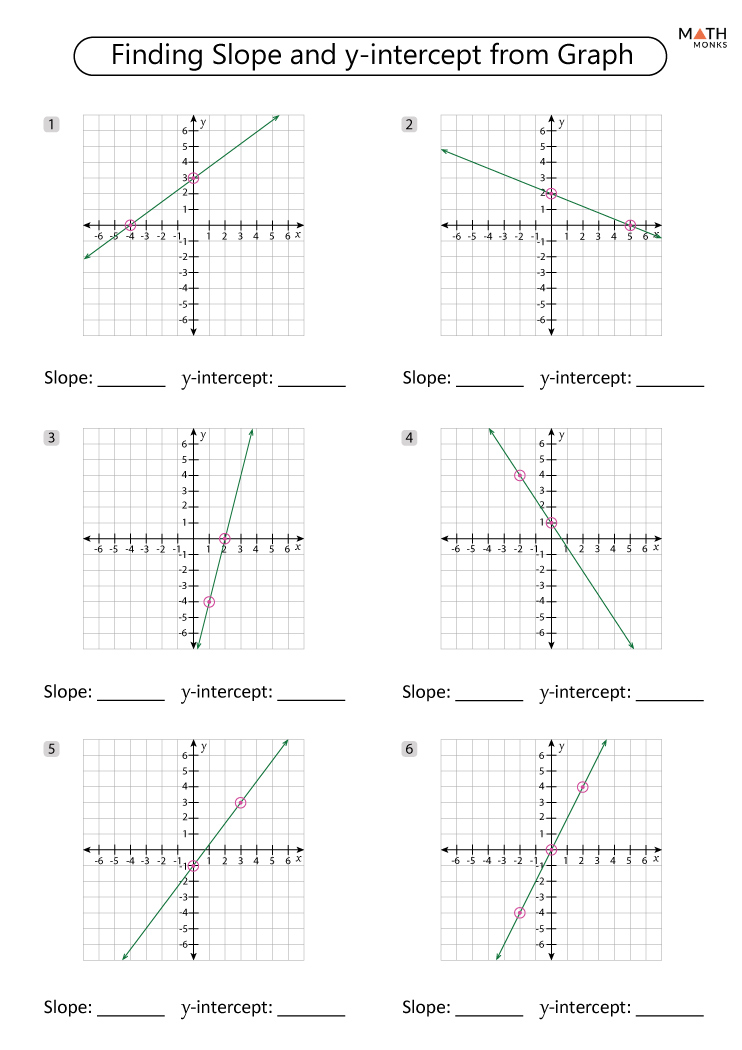
To graph a line using slope intercept form:
Find the y-intercept: Plot the point on the y-axis. If the equation is y = 2x + 3, the y-intercept is at (0,3).
Use the slope: From the y-intercept, move up or down according to the rise, then move left or right according to the run. Continuing with our example, for slope = 2, you would move up 2 units (rise) and then right 1 unit (run) to find another point on the line.
Draw the line: Connect these points to form the line.
Example Problem

Let’s use the equation y = -1/2x + 4:
- The y-intercept is (0, 4), so plot this point.
- The slope is -1/2; you would move down 1 unit (negative slope) and then right 2 units.
- Plot the next point using the slope direction, then connect both points to form the line.
📝 Note: Remember that positive slope goes up from left to right, and negative slopes go down.
Algebra 1 Solutions: Understanding the Process

To excel in Algebra 1, understanding the slope intercept form and its applications is crucial. Here’s how students can work through problems involving this form:
Identify the Slope and y-Intercept: Look at the equation and identify the values for m and b.
Substitute Values: Use the identified values to graph or solve problems.
Convert to Slope Intercept Form: When equations are not given in slope intercept form, use algebraic manipulation to transform them into this form.
Practical Examples

Consider these problems and their solutions:
Convert to Slope Intercept Form:
Equation given: 2x + y = 8
- Subtract 2x from both sides: y = -2x + 8
Here, m = -2 and b = 8.
Solve for a Line’s Equation Given Two Points:
Let’s say we have two points: (2, 5) and (4, 9).
Find slope m: m = (9 - 5)/(4 - 2) = 4⁄2 = 2
Use one point to find b: y = mx + b 5 = 2(2) + b b = 1
So the equation is: y = 2x + 1
Key Takeaways from Slope Intercept Form

As we’ve explored, understanding and applying slope intercept form is essential in algebra. Here are some final points:
- It simplifies graphing lines.
- It provides immediate information about the slope and y-intercept, enhancing problem-solving.
- It’s a foundational concept that appears in higher mathematics and real-life applications, like calculating rates of change or understanding trends.
Wrapping Up

The slope intercept form (y = mx + b) is a powerful tool in algebra that aids in both the conceptual understanding and practical application of linear equations. By mastering this form, students can:
- Quickly graph lines and interpret their behavior.
- Transform equations to reveal slope and y-intercept.
- Solve various problems involving lines with ease.
Remember, practice is key to mastering these skills. Whether solving for slope, finding the y-intercept, or graphing lines, each step with slope intercept form brings you closer to algebra proficiency.
Why is slope important in linear equations?

+
Slope tells us how steep the line is and how the y-value changes with respect to the change in x. This rate of change is crucial for understanding trends, physical slopes, or any scenario where you’re comparing two quantities.
How can I convert an equation from standard form to slope intercept form?

+
To convert from standard form (Ax + By = C) to slope intercept form:
- Isolate the y term by moving x and constants to the other side of the equation.
- Solve for y to get the equation in y = mx + b form.
What does the y-intercept represent?

+
The y-intercept represents the point at which the line crosses the y-axis, where the x-coordinate is zero. It’s the starting value or initial condition for the y-variable in a linear equation.